II.1.3. COUTS ASSOCIES AUX
STOCKS.
Un stock est constitué pour satisfaire une demande
future. En cas de demande aléatoire, il peut y avoir non
coïncidence entre la demande et le stock.
a) Coût de possession.
Les coûts de possession comprennent :
- les coûts de détention d'un article en stock
durant une certaine période en fonction des conditions
financières d'acquisition et des éventuelles conditions de
reprise.
- Les coûts de stockage qui sont les dépenses de
logistique, de conservation du stock
b) Coût de rupture.
Il y a rupture lorsque la demande excède le stock
existant. Les conséquences de cette rupture sont différentes
selon que la demande est interne (le produit stocké est demandé
par une autre entité intérieure à l'entreprise) ou externe
(le produit est destiné à la vente).
En cas de demande externe, la demande non satisfaite peut
être perdue ou reportée :
- Demande perdue (on parle de ventes manquées) le
coût de rupture est le manque à gagner de la non fourniture d'une
unité du produit, généralement la marge
bénéficière sur cet article ;
- Demande reportée (on parle de ventes
différées) le coût de rupture n'inclut pas la marge car la
vente sera réalisée plus tard. Ce coût de rupture est le
coût administratif d'ouverture d'un dossier de prise de commande et
éventuellement un coût commercial.
En cas de demande interne, on parle plus de stock de
distribution, mais bien de stock de fabrication. Dans ce cas, la rupture
entraîne un chômage technique des postes en aval. Ce coût
peut être très important dans une chaîne d'assemblage
travaillant en juste à temps.
c) Les coûts de commande.
- En cas de stock de fabrication, le coût de commande
est le coût de lancement de la production. Normalement ce coût est
indépendant de la quantité fabriquée ;
- En cas de stock d'approvisionnement le coût de
commande est le coût administratif de gestion de la commande :
établissement d'un bordereau, contrôle de livraison, liquidation
comptable.
Normalement, ce coût est également
indépendant de la quantité commandée.
II.1.4. LA GESTION CALENDAIRE
DE STOCK.
On parle de gestion calendaire de stock lorsque l'intervalle
entre deux reconstitutions du stock est fixé. On appelle cet intervalle
la période de révision calendaire, elle est notée T et S
est la variable de commande du système qui est aussi le niveau initial
du stock ou niveau de recomplètement du stock.
a) En rotation nulle.
C'est quand il n'y a pas de report possible des invendus aux
périodes suivantes. Le problème est de trouver le niveau du stock
initial S qui est ici la variable de commande. En effet, la période de
révision calendaire, c'est-à-dire l'intervalle entre deux
approvisionnements, notée T est généralement fixé
par la nature de l'approvisionnement. Ainsi, S sera déterminé de
manière à minimiser :
C(S) = Cp'p(S) + Cr'r(S) + Cc'c (2.1)
Où: C(S): Coût moyen;
Cp : Coût unitaire de possession ;
Cc : Coût unitaire de commande ;
Cr : Coût unitaire de rupture ;
Ir(S) : nombre moyen de demandes non satisfaites ou
nombre moyen de rupture
Ip : Stock moyen possédé au stock moyen
résiduel ;
Ic : Nombre moyen de commandes passées.
Après analyse, il apparaît que le stock optimal
S0 est celui pour lequel le coût de gestion C(S) est
inférieur à celui des stocks immédiatement
inférieur ou supérieur. Ainsi, la diminution de rupture moyenne
Ir(S) occasionnée par une augmentation d'une unité du stock
initial à partir de S est égale à la probabilité
que la demande soit strictement supérieur ou égale au stock
initial S.
D'où : Ir(S + 1) - Ir(S) = - P(X>S) ;
(2.2)
Ip(S) = S - 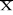 + Ir(S). (2.3) + Ir(S). (2.3)
Qui peut s'interpréter en disant que le stock moyen
résiduel Ip(S) est égal au stock de départ S
diminué de la demande moyenne satisfaite (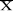 - Ir(S)). En effet si - Ir(S)). En effet si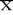 est bien la demande moyenne exprimée, il faut tenir compte de
Ir(S), la rupture moyenne pour en déduire la demande moyenne
satisfaite. est bien la demande moyenne exprimée, il faut tenir compte de
Ir(S), la rupture moyenne pour en déduire la demande moyenne
satisfaite.
La conséquence de la relation (2.3) est que l'on peut
exprimer le coût total C(S) en fonction du seul coût de rupture
Ir :
C(S) = CrIr + CpIp = CrIr + Cp(S -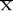 + Ir(S) + Ir(S)
C(S) = Cp(S -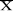 ) + (Cr + Cp)Ir(S) (2.4) ) + (Cr + Cp)Ir(S) (2.4)
Ainsi, c'est (3.4) qui doit être minimisé pour
trouver S0 avec les conditions d'optimalité
suivantes :
Cp - (Cp + Cr) P(X>S0) > 0
Cp - (Cp + Cr) P(X>S0-1) > 0
Où P(X>S0) <  < P(X>S0-1) > 0 (2.5) < P(X>S0-1) > 0 (2.5)
NB : cette valeur est à consulter dans les tables
de poisson.
b) A rotation nulle.
On parle de stocks à rotation nulle lorsque les
invendus d'une période seront vendus aux périodes
suivantes ; ici la commande à passer pour un approvisionnement en
début de période n'est plus fixe. Deux cas sont
possibles :
- Il reste un stock résiduel positif ; dans ce
cas, on demande la différence entre S et le stock
résiduel ;
- Le stock résiduel est nul ; dans ce cas on
demande S augmenté des demandes non satisfaites de la période
précédentes qui ont pu être reportées.
Par des calculs analogues à ceux du cas de la rotation
nulle, on détermine finalement le niveau optimal de
recomplètement. S0 par la formule suivante :
P(X>S0) =  = P(X>S0-1) (2.6) = P(X>S0-1) (2.6)
| 


