5.1.6 2.2.2. Méthodologie de
collecte des données et Traitement
5.1.7 2.2.2.1. Collecte des
données
En statistique, la pertinence des analyses repose sur la
qualité et la fiabilité des données collectées. Au
Bénin, ces données sontdifficiles à collecter etla plus
part du temps, elles sont quasi-inexistantes. Les données sur la
production de l'igname, la superficie emblavée et la hauteur des pluies,
consacrées à l'analyse économétrique faite dans ce
mémoire, initialement annuelles, couvrent la période de 2010
à 2018, ce qui fait neuf (09) observations. Pour plus de pertinence du
modèle économétrique, il a fallu procéder à
une trimestrialisation afin de disposer de plus d'une trentaine d'observations.
Cette trimestrialisation a été réalisée à
l'aide de l'algorithme de Goldstein et Kahn (1976). Ce traitement
d'épuration des données est bien entendu susceptible d'introduire
un biais dans les résultats. Cependant, toutes choses étant
égales par ailleurs, les estimations ont une marge d'erreur acceptable
pour la qualité de l'analyse faite dans cette étude.
Les données sur les prix aux producteurs couvrant la
période de 2010 à 2018 sont des données mensuelles. Nous
avons donc pu obtenir les données trimestrielles en calculant la moyenne
pour chaque trois (03) mois.
La variable « taux de croissance
démographique » a été exceptionnellement
traitée. Le RGPH a été réalisé en 1979,
1992, 2002 et 2013 ; ce qui fait que nous ne disposons pas de
données sur les années transitaires. De 2010 à 2012, nous
avons utilisé les données issues des projections
révisées du RGPH3. Ces projections ont été
révisées en 2008 après l'Enquête
Démographique et de Santé du Bénin, 3ème
édition (EDSB-III) réalisée en 2006. La population de 2013
est celle issue des résultats définitifs du RGPH4. Les
données de2014 à 2018 sont les projections faites à base
du RGPH4. Nous avons ensuite calculé le taux annuel de croissance
démographique avant de faire la trimestrialisation.
De façon globale, les données collectées
sont des séries temporelles de 2010 à 2018 sur la production de
l'igname, la superficie emblavée, le prix aux producteurs, les
précipitations annuelles et le taux de croissance
démographique.
Le tableau suivant résume les informations sur les
données brutes :
Tableau 1 : Informations sur les
données brutes
|
Variables
|
Unité
|
Abréviation
|
Source
|
|
Production de l'igname
|
Tonnes
|
Prod_ign
|
DSA
|
|
Superficie emblavée
|
Hectare
|
Sup_emb
|
DSA
|
|
Prix aux producteurs
|
F CFA
|
Prix_prod
|
INSAE
|
|
Taux de croissance démographique
|
%
|
Croi_demo
|
INSAE
|
|
Hauteur des pluies
|
mm
|
Haut_Pluie
|
INSAE
|
Source : Etabli par les auteurs, 2020
Algorithme de Goldstein et Kahn (1976)
Considérons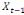 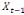 , , 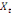 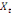 , ,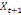 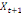 trois observations annuelles successives de la variable X. Si la
fonction quadratique qui passe par ces trois points (cf.
THEOREMED'EUCLIDE) est telle que : trois observations annuelles successives de la variable X. Si la
fonction quadratique qui passe par ces trois points (cf.
THEOREMED'EUCLIDE) est telle que :
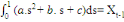 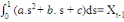 (1) (1)
 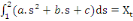 (2) (2)
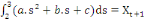 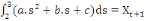 (3) (3)
Alors, on peut déterminer les paramètres a, b et
c, en calculant d'abord les intégrales de (1) à (3), puis en
résolvant le système d'équations suivant :
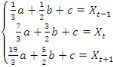 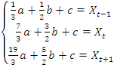 (4) (4)
La résolution de ce système conduit au
résultat suivant :
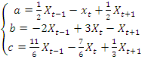 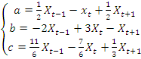 (5) (5)
A partir des valeurs des paramètres de la fonction
quadratique ainsi obtenues, les quatre observations trimestrielles de
l'année t peuvent être calculées en utilisant les formules
d'interpolation suivantes :
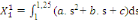 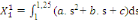 (6) (6)
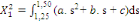 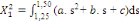 (7) (7)
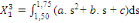 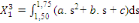 (8) (8)
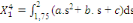 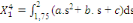 (9) (9)
Les calculs algébriques effectués sur les
expressions (6) à (9) ci-dessus dans lesquelles l'on aurait au
préalable remplacé les paramètres a, b et c par leur
expression de (5), conduisent enfin aux données d'interpolation
trimestrielles suivantes :
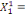 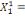 0 ,05468 0 ,05468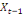 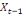 + 0,23438 + 0,23438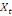 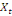 - 0,039067 - 0,039067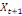 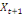 (10) (10)
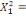 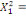 0,00781 0,00781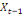 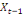 + 0,26563 + 0,26563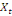 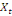 - 0,02344 - 0,02344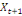 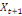 (11) (11)
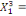 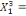 -0,02344 -0,02344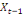 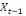 + 0,26562 + 0,26562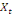 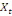 + 0,00781 + 0,00781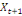 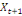 (12) (12)
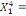 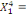 -0,03910 -0,03910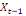 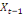 + 0,23437 + 0,23437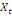 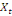 + 0,05469 + 0,05469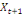 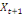 (13) (13)
La série trimestrielle obtenue peut être
ramenée à une série annuelle par sommation des
observations des quatre trimestres de chaque année. En effet,
d'après la relation de Chasles, l'on a :
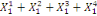 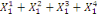 = = 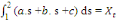 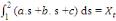 (14) (14)
| 


