5.1.8 2.2.2.2. Outils et modèle
d'analyse
Les méthodes utilisées dans cette étude
sont à la fois descriptives et explicatives. Pour décrire
l'évolution des variables, nous employons les méthodes
descriptives. Par contre, pour tester les hypothèses émises, nous
utilisons les méthodes explicatives.
5.1.9 2.2.2.2.1. Méthodes
descriptives
Toutes les variables intervenant dans le cadre de cette
étude sont des séries temporelles. C'est pourquoi, après
avoir donné leurs caractéristiques descriptives (moyenne,
écart-type, variance, ...) et réalisé la boîte
à moustaches, nous avons analysé successivement, à l'aide
du logiciel Excel, l'évolution au cours du temps de la production
d'igname, de la superficie emblavée, des prix aux producteurs, de la
hauteur des pluies, de la température et de la population rurale dans le
département du Borgou.
Boîte à moustaches
La boîte à moustaches, une traduction de Box
& Whiskers Plot, est une invention de TUKEY (1977) pour représenter
schématiquement la distribution d'une variable.
Cette représentation graphique peut être un moyen
pour approcher les concepts abstraits de la statistique, si l'on pratique son
usage sur différents jeux de données.
Le terme spécifique Box & Whiskers
Plot et le terme générique Box Plot recouvrent
une grande variété de diagrammes en forme de boîtes qui se
différencient par leur construction, leurs interprétations, et
leurs usages. E. HORBER qui a effectué des recherches bibliographiques
sur ce thème a repéré une soixantaine de formes et de
constructions différentes.
Dans le cadre de notre étude, nous avons
réalisé les boîtes à moustaches sur eviews 9.
Chacune de ces boîtes comprend :
· les quartiles Q1, Q2 (médiane) et Q3 ;
· les extrémums (minimum et maximum) de la
distribution ;
· la moyenne ;
· les moustaches inférieure et
supérieure ;
· l'extrémité de la moustache
inférieure notée Front.Basse
(Front.Basse=Q1-1,5*(Q3-Q1)) ;
· l'extrémité de la moustache
supérieure notée Front.Haute
(Front.Haute=Q3+1,5*(Q3-Q1))
· l'écart interquartile
Q3-Q1 ;
· les valeurs dites extrêmes, atypiques,
exceptionnelles, (outliers) situées au-delà des frontières
et représentées par des marqueurs (carré, ou
étoile, etc.).
5.1.10 2.2.2.2.2.
Méthodes explicatives
Détection de la saisonnalité
Pour détecter une éventuelle saisonnalité
de chaque série, nous avons procédé d'abord au test de
Buys Ballot qui permet de voir si le modèle de la variable
considérée est additif ou multiplicatif. Pour cela, on
procède à une régression, pour chaque variable, de son
écart-type sur sa moyenne. Si le coefficient de la moyenne n'est pas
significativement différent de zéro (0), on accepte
l'hypothèse d'un modèle additif. Dans le cas contraire, le
modèle est multiplicatif.
Une fois le choix du type de modèle fait, pour
vérifier la saisonnalité de la série, on admet les
hypothèses suivantes :
H0 : Pas de
saisonnalité
H1 :
Présence de saisonnalité
On calcule alors la statistique de Fisher :
F=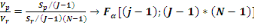 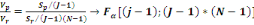
Où 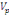 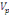 désigne la variance des périodes et désigne la variance des périodes et 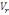 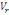 la variance des résidus. la variance des résidus.
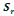 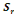 = =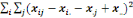 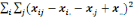
Règle de décision : Si
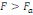 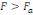 , on rejette l'hypothèse nulle H0 et donc il y a
saisonnalité. , on rejette l'hypothèse nulle H0 et donc il y a
saisonnalité.
Désaisonnalisation
Dans le cas d'une série affectée d'un mouvement
saisonnier, il convient de la retirer préalablement à tout
traitement statistique. Cette saisonnalité est ajoutée à
la série prévue à la fin du traitement afin d'obtenir une
prévision en terme brut.
Les tests de stationnarité
Une série temporelle dont la moyenne (mobile) et/ou la
variance dépendent du temps est dite non stationnaire. Cette non
stationnarité (du type déterministe ou stochastique), si elle
n'est pas traitée (stationnarisation), peut conduire à des
régressions « fallacieuses ». Plusieurs tests aident à
vérifier le caractère stationnaire ou non (existence d'une racine
unitaire) d'une série : test d'Augmented Dickey-Fuller/ADF, test de
Phillips-Perron/PP, test d'Andrews et Zivot/AZ, test Ng-Perron, KPSS,
Ouliaris-Park-Perron, Eliott-Rothenberg-Stock, etc. De tous ces tests, les
trois premiers sont faciles d'application et couramment utilisés. En
fait, le test ADF est efficace en cas d'autocorrélation des erreurs, le
test PP est adapté en présence
d'hétéroscédasticité, et le test AZ est
utilisé pour une série qui accuse une rupture de structure ou
changement de régime identifié de façon endogène.
Dans cette étude, nous avons fait recours aux tests ADF,PP et AZ.
Le modèle Auto Régressif à
Décalage Temporel (ARDL) de Pesaran et al. (2001)
Les modèles « AutoRegressive Distributed Lag/ARDL
», ou « modèles autorégressifs à
retards
échelonnés ou distribués/ARRE » en français,
sont des modèles dynamiques. Ces
derniers ont la particularité
de prendre en compte la dynamique temporelle (délai
d'ajustement,
anticipations, etc.) dans l'explication d'une variable (série
chronologique),
améliorant ainsi les prévisions et
efficacité des politiques (décisions, actions, etc.),
contrairement au modèle simple (non dynamique) dont l'explication
instantanée (effet
immédiat ou non étalé dans le
temps) ne restitue qu'une partie de la variation de la variable
à
expliquer. S'il est soulevé une certaine incertitude en ce qui a trait
à l'ordre réel d'intégration des variables soit à
cause de la présence de ruptures structurelles, soit pour une raison, la
méthodologie ARDL Bound testing et le modèle à correction
d'erreur qui y est dérivé va être utilisé (USAI,
Haïti, 2017). Pesaran et al.(2001)ont défini l'approche Auto
Regressive Distributed Lag (ARDL) en prenant en compte les insuffisances du
modèle VAR. Cette approche a été utilisée dans de
nombreuses études (Wolde Rufael, 2006 ; Squalli, 2007 ;
Akinlo, 2008 ; Odhiambo, 2009 ; Ouedrago, 2010).
Un ARDL est une régression des moindres carrés
contenant des retards de la variable dépendante et des variables
indépendantes. Habituellement, on note ARDL (p, q1, ...,
qk), où p désigne le nombre de retards de la variable
dépendante, qk le nombre de retards de la k-ième
variable explicative. Dans le cadre de notre étude, le modèle
ARDL où chaque variable est supposée stationnaire se
spécifie comme suit :
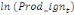 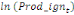 = =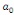 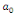 + +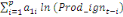 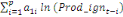 + +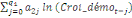 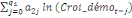 + +
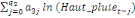 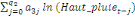 + +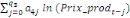 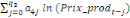 + +
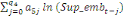 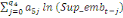 + +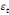 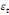 (a) (a)
Par ailleurs, Pesaran et al. (2001) ont
développé une nouvelle approche pour tester l'existence d'une
relation de long terme entre des variables caractérisées par un
ordre d'intégration différent. Il s'agit du test des limites
« bounds tests » pour une relation de long terme dans un
modèle autorégressif à retards échelonnés
(ARDL). A cause de la flexibilité qu'elle offre, cette technique est de
plus en plus utilisée comme alternative aux tests de
cointégration usuels (test de cointégration d'Engle et Granger
(1987) et de Johansen (1988, 1991) en raison de son caractère
contraignant. En effet, le test développé par Pesaran et al.
(2001) ne nécessite pas que les variables du modèle soient
purement I (0) ou I (1).Cette technique est mieux adaptée aux petits
échantillons et offre la possibilité de traiter conjointement la
dynamique de long terme et les ajustements de court terme. On utilise la
statistique de Wald ou la statistique de Fisher pour tester la
significativité de retards des variables en prenant en
considération la contrainte d'un Modèle à Correction
d'Erreur (MCE). L'approche de Pesaran et al. Se fait en plusieurs
étapes.
Dans un premier temps, on estime un Modèle à
Correction d'Erreur (MCE).
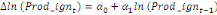 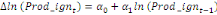 + +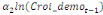 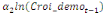 + +
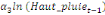 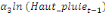 + +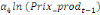 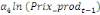 + +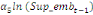 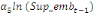
+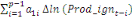 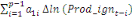 + +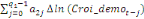 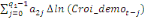 + +
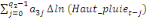 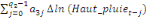 + +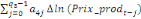 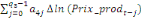
+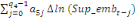 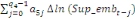 + +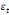 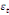 (b) (b)
Où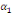 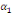 , ,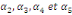 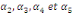 sont les multiplicateurs de long terme ; sont les multiplicateurs de long terme ; 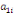 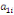 , , 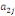 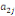 , ,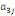 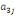 , ,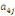 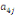 et et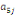 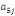 sont les coefficients de la dynamique de court terme ; les
paramètres sont les coefficients de la dynamique de court terme ; les
paramètres  , ,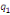 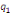 , ,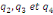 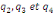 sont les ordres du modèle ARDL et sont les ordres du modèle ARDL et 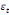 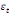 est un bruit blanc non autocorrélé avec est un bruit blanc non autocorrélé avec 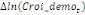 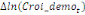 , ,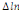 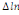 ( (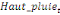 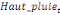 ), ), 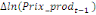 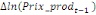 , , 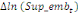 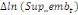 et avec les valeurs retardées de et avec les valeurs retardées de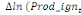 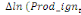 ), ),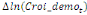 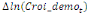 , ,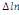 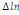 ( (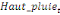 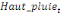 ), ), 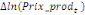 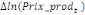 , ,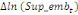 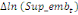 . .
Après avoir vérifié l'absence
d'autocorrélation des résidus, on procède au test de
significativité jointe des multiplicateurs de long terme 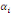 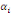 en utilisant le test de Fisher. en utilisant le test de Fisher.
  = =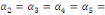 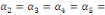 0 (Absence de cointégration) 0 (Absence de cointégration)
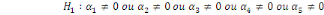 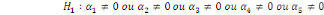 (Présence de cointégration). (Présence de cointégration).
Pesaran et al. (2001) montrent que la statistique
calculée ne suit pas une loi standard.Ils ont simulé deux
ensembles de valeurs critiques pour cette statistique, avec plusieurs cas
(selon qu'on introduit une constante et/ ou une tendance) et différents
seuils. Le premier ensemble correspond au cas où toutes les variables du
modèle sont stationnaires c'est-à-dire I(0) et représente
la borne inférieure ; le second ensemble correspond au cas
où toutes les variables du modèle sont intégrées
d'ordre un I(1) et représente la borne supérieure. Pour conclure
le test, on compare la statistique du test de Fisher aux deux bornes. Si les
F-statistiques calculées se trouvent au-dessus de la valeur critique
supérieure, l'hypothèse nulle d'absence de cointégration
est rejetée. Si les F-statistiques calculées se trouvent
au-dessous de la valeur critique inferieure, le test échoue donc
à rejeter l'hypothèse nulle traduisant une absence de
cointégration. Si les F-statistiques font partie de la bande, alors le
test est non conclusif. Ici nous utiliserons la table des valeurs critiques
proposées par Narayan (2005) pour des tailles d'échantillons
réduits pour plus de précision.
En présence de cointégration, les relations de
long terme sont obtenues par annulation des variables en différences
(Morley, 2006 ; Antonis, Katrakilidis et Persefoni, 2013).
Sur la base de l'équation (b), nous déduisons
qu'elles sont représentées par l'équation :
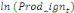 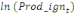 =- =-  - -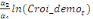 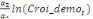 - -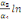 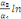 ( (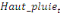 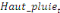 )- )- 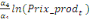 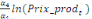
- 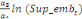 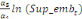 (c) (c)
A partir de cette relation de longue période, le terme
de correction d'erreur (ECT) peut être calculé.
Pour l'équation (c), il est égal à :
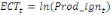 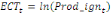 - [- - [-  - -  - -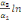 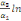 ( (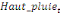 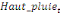 ) )
-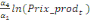 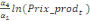 - -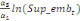 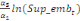 ] ]
L'inclusion de l'ECT retardée d'une période dans
l'équation des effets de court terme permet d'obtenir des estimations
non biaisées et de rendre compte de la vitesse d'ajustement de la
variable dépendante vers sa valeur d'équilibre (Engle et Granger,
1987). En présence de cointégration, les effets de court terme
seront par conséquent examinés sur la base de l'équation
suivante :
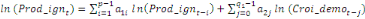 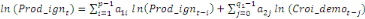 + +
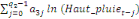 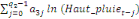 + +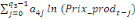 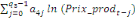 + +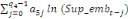 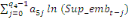
+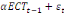 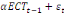 (d) (d)
où 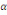 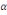 est un coefficient associé au terme ECT et qui
représente, en effet, la vitesse d'ajustement du modèle vers son
équilibre de long terme. Lorsque l'hypothèse de
cointégration est rejetée, les effets ne seront testés que
dans le court terme et les estimations seront basées sur la
modélisation VAR où p sera le retard optimal,
déterminé par de différents critères : est un coefficient associé au terme ECT et qui
représente, en effet, la vitesse d'ajustement du modèle vers son
équilibre de long terme. Lorsque l'hypothèse de
cointégration est rejetée, les effets ne seront testés que
dans le court terme et les estimations seront basées sur la
modélisation VAR où p sera le retard optimal,
déterminé par de différents critères :
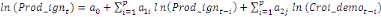 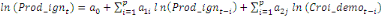 + +
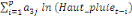 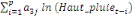 + +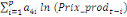 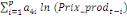 + +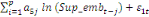 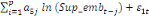
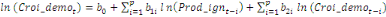 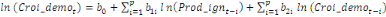 + +
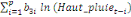 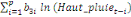 + +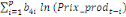 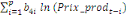 + +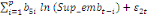 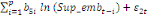
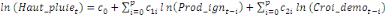 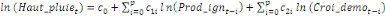 + +
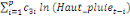 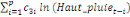 + +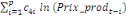 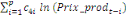 + +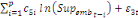 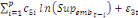
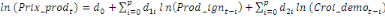 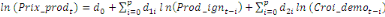 + +
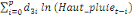 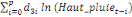 + +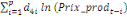 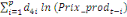 + +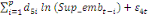 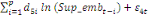
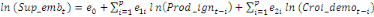 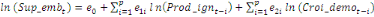 + +
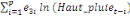 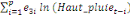 + +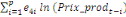 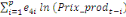 + +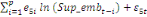 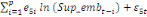
Ce test de cointégration de Pesaran et al. (2001) est
utilisé pour déterminer les relations de long terme entre la
production de l'igname et la population rurale, la hauteur des pluies, le prix
aux producteurs et la superficie emblavée.
Tests de validation ou de robustesse du
modèle
Il s'agit de vérifier notamment que les résidus
du modèle ARDL estimé vérifient les
propriétés requises pour que l'estimation soit valide. Les tests
appropriés sont les tests d'absence d'autocorrélation, de
normalité, d'hétéroscédasticité et de
stabilité.
Vérification des hypothèses
Les hypothèses formulées dans le cadre de cette
étude seront confirmées lorsque les coefficients des variables
considérées du modèle ARDL estimé remplissent
certaines conditions, comme l'indique le tableau suivant :
Tableau 2 : Conditions de confirmation des
hypothèses
|
Hypothèses
|
Conditions
|
Décision
|
|
Hypothèse 1
|
si la probabilité associée au coefficient de la
superficie emblavée est supérieure à 5% et le coefficient
de la superficie emblavée est positif
|
Confirmée
|
|
Hypothèse 2
|
si la probabilité associée au coefficient de la
hauteur des pluies est supérieure à 5%
|
Confirmée
|
|
Hypothèse 3
|
si la probabilité associée au coefficient de la
croissance démographique est supérieure à 5%
|
Confirmée
|
Source : Etabli par les auteurs, 2020
| 


