6.1.14 3.2.3.3.
Test de cointégration aux bornes
Le test de cointégration de Pesaran et al. (2001) exige
que le modèle ARDL soit estimé au préalable. La
statistique du test calculée, soit la valeur F de Fisher, sera
comparée aux valeurs critiques (qui forment des bornes). Si la
statistique de Fisher est supérieure à la borne
supérieure, il y a cointégration. Il n'existe pas de
cointégration lorsque la statistique de Fisher est inférieure
à la borne supérieure. Cependant, on ne saurait conclure lorsque
la statistique de Fisher est strictement comprise entre les deux bornes.
Les résultats du test de cointégration aux
bornes confirment, au seuil de 1%, 2,5%, 5% et 10%, l'existence d'une relation
de cointégration entre les séries sous étude (la
valeur de F-stat est supérieure à celle de la borne
supérieure), ce qui donne la possibilité d'estimer les
effets de long terme delprod_ign, lcroi_demo, lhaut_pluie, lprix_prod,
lsup_emb.
Tableau 9 : Résultats du test de
cointégration de Pesaran et al. (2001)
|
Variables
|
Dlprod_ign, Dlcroi_demo, lhaut_pluie, Dlprix_prod,
Dlsup_emb
|
|
F-stat calculée
|
116,9155
|
|
K
|
4
|
|
Seuil critique
|
Borne inférieure
|
Borne supérieure
|
|
10%
|
2,45
|
3,52
|
|
5%
|
2,86
|
4,01
|
|
2.5%
|
3,25
|
4,49
|
|
1%
|
3,74
|
5,06
|
Source : Etabli par les auteurs, 2020
6.1.15 3.2.3.4.
Coefficients de Long terme et dynamique de court terme
6.1.16 3.2.3.4.1.
Coefficients de court terme (CT)
Comme on peut le lire sur le tableau 10 ci-dessous, le
coefficient d'ajustement ou force de rappel est statistiquement significatif et
négatif, ce qui garantit un mécanisme de correction d'erreurs, et
donc l'existence d'une relation de long terme (cointégration) entre
variables. Par ailleurs, le coefficient associé à la superficie
emblavée ainsi que celui associé aux prix aux producteurs sont
significativement différents de zéro (0) à court terme.
Par contre, la hauteur des pluies et la croissance démographique
présentent des coefficients non significatifs à court terme.
Aussi, l'on note ce qui suit :
§ les prix aux producteurs ont un impact positif sur la
production de l'igname dans le département du Borgou à CT :
une augmentation des prix aux producteurs de 1% entraine une hausse de 0,58% de
la production de l'igname. Mais un an en arrière les prix aux
producteurs constituaient un frein à la production de l'igname dans le
Borgou.
§ La superficie emblavée exerce un effet positif
sur la production de l'igname à court terme : un accroissement de la
superficie emblavée de 1% accélère la production de
l'igname de 3,08% à CT. Ces effets s'inversent plutôt dans le
temps : l'accroissement de la superficie il y a 3 ans a été un
frein à la production de l'igname dans le Borgou.
Tableau 10 :Résultats d'estimation
des coefficients de CT
|
Variable dépendante : LPROD_IGN
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
D(LPROD_IGN(-1))
|
2,248975
|
0,469416
|
4,791008
|
0,0020
|
|
D(LPROD_IGN(-2))
|
1,906765
|
0,456285
|
4,178889
|
0,0041
|
|
D(LPROD_IGN(-3))
|
1,268771
|
0,334243
|
3,795955
|
0,0068
|
|
D(LCROI_DEMO)
|
0,142368
|
0,066277
|
2,148073
|
0,0688
|
|
D(LCROI_DEMO(-1))
|
-0,079584
|
0,086065
|
-0,924697
|
0,3859
|
|
D(LCROI_DEMO(-2))
|
-0,184529
|
0,090298
|
-2,043565
|
0,0803
|
|
D(LCROI_DEMO(-3))
|
0,105825
|
0,059504
|
1,778457
|
0,1186
|
|
D(LHAUT_PLUIE)
|
-0,532717
|
0,427411
|
-1,246381
|
0,2527
|
|
D(LHAUT_PLUIE(-1))
|
-1,767428
|
0,621398
|
-2,844277
|
0,0249
|
|
D(LPRIX_PROD_SA)
|
0,577667
|
0,233537
|
2,473561
|
0,0426
|
|
D(LPRIX_PROD_SA(-1))
|
-0,828726
|
0,342173
|
-2,421949
|
0,0460
|
|
D(LPRIX_PROD_SA(-2))
|
-0,023188
|
0,259251
|
-0,089442
|
0,9312
|
|
D(LPRIX_PROD_SA(-3))
|
0,286015
|
0,206509
|
1,384998
|
0,2086
|
|
D(LSUP_EMB)
|
3,082190
|
0,630200
|
4,890815
|
0,0018
|
|
D(LSUP_EMB(-1))
|
-0,309545
|
0,624181
|
-0,495922
|
0,6351
|
|
D(LSUP_EMB(-2))
|
0,270879
|
0,643757
|
0,420779
|
0,6865
|
|
D(LSUP_EMB(-3))
|
-4,200060
|
1,099041
|
-3,821568
|
0,0065
|
|
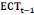 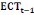
|
-2,82833
|
0,549047
|
-5,151343
|
0,0000
|
Source : Etabli par les auteurs, 2020
|
|



