6.1.13 3.2.3.2.
Estimation du modèle ARDL(4,4,4,0,4)
Les résultats d'estimation révèlent que
les coefficients dont les probabilités sont en gras sont
significativement différents de zéro (0) au seuil de 5%. Avec une
qualité d'ajustement meilleure, la production de l'igname dans le
département du Borgou est expliquée à hauteur de 97% par
les variables mis en jeu. La probabilité de la Statistique de Fisher
(0,0000) révèle qu'au seuil de 5%, le modèle
ARDL(4,4,4,0,4) est globalement significatif. Par ailleurs, le R2
(0,991511) est inférieur à la statistique de Durbin-Watson
(1,26632). D'après la règle de Granger, le modèle est de
bonne régression et toutes les variables utilisées dans cette
étude sont effectivement stationnaires.
Tableau 6 : Modèle
ARDL(4,4,4,0,4)
|
Variable dépendante : DLPROD_IGN
|
|
Variables
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
DLPROD_IGN(-1)
|
0 ,064360
|
0,053424
|
1,204691
|
0,2561
|
|
DLPROD_IGN(-2)
|
0,019151
|
0,054918
|
0,348723
|
0,7345
|
|
DLPROD_IGN(-3)
|
0,018592
|
0,052612
|
0,353372
|
0,7311
|
|
DLPROD_IGN(-4)
|
-1,543464
|
0,091120
|
-16,93879
|
0,0000
|
|
DLCROI_DEMO
|
-0,032270
|
0,009264
|
-3,483481
|
0,0059
|
|
DLCROI_DEMO(-1)
|
-0,011607
|
0,011131
|
-1,042756
|
0,3216
|
|
DLCROI_DEMO(-2)
|
-0,004771
|
0,010051
|
-0,474723
|
0,6452
|
|
DLCROI_DEMO(-3)
|
-0,000614
|
0,009557
|
-0,064282
|
0,9500
|
|
DLCROI_DEMO(-4)
|
0,024060
|
0,006550
|
3,673370
|
0,0043
|
|
LHAUT_PLUIE
|
-1,390484
|
0,158660
|
-8,763935
|
0,0000
|
|
LHAUT_PLUIE(-1)
|
1,371894
|
0,205427
|
6,678245
|
0,0001
|
|
LHAUT_PLUIE(-2)
|
-0,011249
|
0,132359
|
-0,084988
|
0,9339
|
|
LHAUT_PLUIE(-3)
|
-0,212337
|
0,144371
|
-1,470771
|
0,1721
|
|
LHAUT_PLUIE(-4)
|
0,209146
|
0,132851
|
1,574290
|
0,1465
|
|
DLPRIX_PROD_SA
|
-0,004504
|
0,039887
|
-0,112923
|
0,9123
|
|
DLSUP_EMB
|
1,600459
|
0,124269
|
12,87898
|
0,0000
|
|
DLSUP_EMB(-1)
|
-0,240322
|
0,100433
|
-2,392853
|
0,0378
|
|
DLSUP_EMB(-2)
|
-0,157039
|
0,097723
|
-1,606985
|
0,1391
|
|
DLSUP_EMB(-3)
|
-0,274448
|
0,113471
|
-2,418653
|
0,0361
|
|
DLSUP_EMB(-4)
|
2,499742
|
0,185316
|
13,48908
|
0,0000
|
|
C
|
0,174851
|
0,396457
|
0,441033
|
0,6686
|
|
R-carré
|
0,991511
|
F-statistic
|
58,39657
|
|
R-carré ajusté
|
0,974532
|
Prob(F-statistic)
|
0,000000
|
|
|
|
Durbin-Watson stat
|
1,26632
|
Source : Etabli par les auteurs, 2020
Le tableau suivant est le récapitulatif des tests de
robustesse du modèle ARDL(4,4,4,0,4) ainsi estimé :
Tableau 7 : Résultats des tests
diagnostiques du modèle ARDL estimé
|
Hypothèse du test
|
Tests
|
Valeurs (probabilité)
|
|
Autocorrélation
|
Breusch-Godfrey
|
2,203453 (0,1729)
|
|
Hétéroscédasticité
|
Breusch-Pagan-Godfrey
|
0,468866 (0,9283)
|
|
Normalité
|
Jarque-Bera
|
0,649362 (0,7228)
|
|
Spécification
|
Ramsey (Fisher)
|
0,125214 (0,7316)
|
Source : Etabli par les auteurs, 2020
L'hypothèse nulle est acceptée pour tous ces
tests. De ce fait, l'on note l'absence d'autocorrélation des erreurs,
l'absence d'hétéroscédasticité, la normalité
des erreurs, et la bonne spécification du modèle. Notre
modèle est ainsi validé sur le plan statistique.
Le modèle ARDL(4,4,4,0,4) estimé est globalement
bon et explique à 97% la production de l'igname dans le
département du Borgou, de 2010 à 2018.La spécification du
modèle est la suivante :
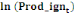 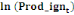 = =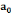 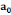 + +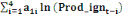 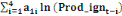 + +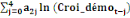 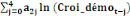 + +
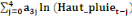 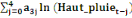 + +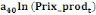 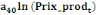 + +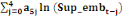 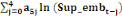 + +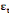 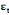
Où les valeurs des coefficients sont consignées
dans le tableau suivant :
Tableau 8 : Valeurs descoefficients du
modèle ARDL(4,4,4,0,4)
|
Coefficients
|
Valeurs
|
|
Coefficients
|
Valeurs
|
|
Coefficients
|
Valeurs
|
|
0,174851
|
|
|
-0,004771
|
|
|
0,209146
|
|
0,064360
|
|
|
-0,000614
|
|
|
-0,004504
|
|
0,019151
|
|
|
0,024060
|
|
|
1,600459
|
|
0,018592
|
|
|
-1,390484
|
|
|
-0,240322
|
|
-1,543464
|
|
|
1,371894
|
|
|
-0,157039
|
|
-0,032270
|
|
|
-0,011249
|
|
|
-0,274448
|
|
-0,011607
|
|
|
-0,212337
|
|
|
2,499742
|
Source : Etabli par les auteurs, 2020
|
|



