6.1.10 3.2.2.
Analyse de la stationnarité des séries
L'analyse de la stationnarité des séries a
été faite grâce aux tests d'Augmented Dickey-Fuller/ADF, de
Phillips-Perron/PP et d'Andrews et Zivot/AZ. Les résultats de ces tests
sont récapitulés dans le tableau 4. L'on note que les
séries production de l'igname, croissance démographique, prix aux
producteurs et superficie emblavée sont intégrées d'ordre
1 (stationnaire après la première différence), alors que
la série hauteur des pluies reste stationnaire à niveau (sans
différenciation). Les séries sont ainsi intégrées
à des ordres différents ; ce qui rend inefficace le test de
cointégration de Engle et Granger (applicable à deux
séries intégrées de même ordre) et celui de Johansen
(applicable à plusieurs séries intégrées de
même ordre) et rend opportun le test de cointégration aux bornes
(Pesaran,2001).
Tableau5 : Résultats des tests de
stationnarité des séries
|
Variables
|
Niveau
|
Différence première
|
Différence deuxième
|
Constat
|
|
ADF
|
PP
|
AZ
|
ADF
|
PP
|
AZ
|
ADF
|
PP
|
AZ
|
|
LPROD_IGN
|
-1,4689
|
-1,8742
|
-4,9215
|
-1,6737
|
-3,6189**
|
-5,0553
|
-3,05674
|
-
|
-6,8971**
|
I(1)
|
|
(0,8143)
|
(0,6463)
|
(0,0930)
|
(0,7339)
|
(0,0430)
|
(0,0693)
|
(0,0528)
|
(0,01)
|
|
LCROI_DEMO
|
-3,0246
|
-3,059447
|
-4,7479
|
-6,6086*
|
-6,6309*
|
-6,8224**
|
-
|
-
|
-
|
I(1)
|
|
(0,1402)
|
(0,1315)
|
(0,1407)
|
(0,0000)
|
(0,0000)
|
(0,01)
|
|
LHAUT_PLUIE
|
1,2188
|
-2,1236
|
-5,1921**
|
-1,9836
|
-4,1005**
|
-
|
-4,0602**
|
-
|
-
|
I(0)
|
|
(0,9999)
|
(0,5153)
|
(0,0481)
|
(0,5827)
|
(0,0144)
|
(0,0191)
|
|
LPRIX_PROD
|
-2.3882
|
-2,3984
|
-3,7128
|
-5,4861*
|
-6,1424*
|
-5,8901**
|
-
|
-
|
|
I(1)
|
|
(0.3789)
|
(0,3739)
|
(0,6998)
|
(0,0005)
|
(0,0001)
|
(0,01)
|
|
|
LSUP_EMB
|
-2,2433
|
-2,2866
|
-3,9748
|
-1,8427
|
-3,3068
|
-8,6217**
|
-5,2608*
|
-7,3585*
|
-
|
I(1)
|
|
(0,4478)
|
-0,4298
|
(0,5392)
|
(0,6545)
|
(0,0822)
|
(0,01)
|
(0,0013)
|
(0,0000)
|
Source : Etabli par les auteurs, 2020
NB : (.) : Probabilités ; * :
Stationnaires à 1% ; ** : Stationnaires à 5%
6.1.11 3.2.3.
Estimation du modèle ARDL
6.1.12 3.2.3.1.
Spécification du modèle ARDL
La modélisation par l'approche ARDL exige pour chaque
variable, la détermination du retard optimal. Nous nous sommes servis du
Critère d'Information d'Akaike (AIC) pour sélectionner le
modèle ARDL optimal, celui qui offre des résultats
statistiquement significatifs. Ci-dessous, les vingt (20) meilleurs
modèles parmi les deux mille cinq cent(2500) modèles
évalués :
Figure 6 : Retards optimaux des séries
selon le Critère d'Information d'Akaike
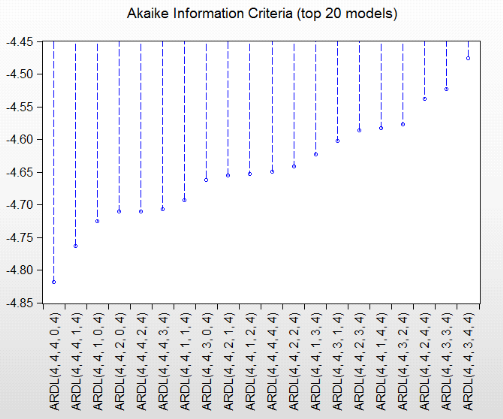
Source : Etabli par les auteurs, 2020
Comme on peut le voir, le modèle ARDL (4,4,4,0,4) est
le plus optimal parmi les 20 présentés, car il offre la plus
petite valeur du AIC.
|
|



