Gestion des stocks dans un réseau de distribution en adoptant plusieurs moyens de transport.

3.2.2 Exemple sous LINGO

Nous allons vous présenter un exemple pour un Modèle de transport qui montre comment écrire un modèle sous la forme compacte sur LINGO.

L'Entrepôt		La Capacité	Reno
35		Chicago
25		Newark
21

Tableau 3.1 : la capacité de chaque entrepôt

Le Client		La Demande	San Francisco
15		Dallas
17		St. Louis
22		Miami
12

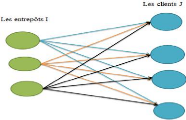
Tableau 3.2 : la demande de chaque clients

Figure 3.1 : la relation entre les entrepôts et les clients

Tableau 3.3:le coût unitaire entre les entrepôts et les clients

San Francisco

Dallas

St. Louis

2

6

7

6

4

2

9

5

4

Le coûtunitaire

			Miami	Reno
			10	Chicago
			6	Newark
			5

Pour rédiger le problème qui permet de trouver la quantité à acheminer entre les sitesil faut commencer à définir : les ensembles, les paramètres, les variables de décision, la fonction objectif et les contraintes.

Chapitre 03 : Evaluation de réseau de transport

· Les ensembles

> I: ensemble des entrepôts

> J: ensemble des clients

· Les paramètres

> Xij: Volume transporté entre l'entrepôt i et le clientj > Cij: coût de transport entre l'entrepôt i et le client j > Bi : capacité de l'entrepôt i

> Aj : la demande du client j

· La fonction objectif

Cij

X ij

3 4

Min ?? Z =

i=1 j

= 1

· Les contraintes Contraintes de demande

3 ? X = Aj,?j ij i=1 Contraintes de capacité 4

{ 1,2,3,4}

? X = bi , ? i ij

=

{ 1,2,3 }

j=1 Structure des données sur LINGO · Les ensembles et les variables de décision SETS: ENTREPOT /E1, E2, E3/: Capacite;
			Paramètres
					Client /C1, , C3, C4/ :
	DEMANDE;					ROUTES ( ENTREPOT, Client)
: Cout,	VOLUME;	Variables de décision
						[OBJ] MIN = @SUM( ROUTES :
Cout *	VOLUME);

· Contraintes

- De demande

!la demande de client;

@FOR (Client (J): [DEM]@SUM(ENTREPOT(I): VOLUME (I,J))>= DEMANDE(J));

- De capacité

!satisfaction du besoin de client;

@FOR (ENTREPOT (I): [SUP]@SUM(Client(J): VOLUME (I,J))<= Capacite(I));

Lemodèlecomplet

MODEL:

!3 entrepôts, 4 clients,problème de transport;

SETS:

ENTREPOT /E1, E2, E3/: Capacite;

Client /C1, , C3, C4/ : DEMANDE;

ROUTES ( ENTREPOT, Client) : Cout, VOLUME;

ENDSETS

!la fonction objective;

[OBJ] MIN = @SUM( ROUTES : Cout * VOLUME);

!la demande de client;

@FOR (Client (J): [DEM]@SUM(ENTREPOT(I): VOLUME (I,J))>= DEMANDE(J));

!satisfaction du besoin de client;

@FOR (ENTREPOT (I): [SUP]@SUM(Client(J): VOLUME (I,J))<= Capacite(I));

Chapitre 03 : Evaluation de réseau de transport

!les parametres ;

DATA:

Capacite = 30, 25, 21; DEMANDE = 15, 17, 22, 12;

Cout = 6, 2, 6, 7,

4, 9, 5, 3,

8, 8, 1, 5;

ENDDATA END

· Solution donnée par LINGO

Global optimal solution found.

Objective value: 161.0000

Total solver iterations: 0

Variable Value Reduced Cost

CAPACITE( E1) 30.00000 0.000000

CAPACITE( E2) 25.00000 0.000000

CAPACITE( E3) 21.00000 0.000000

DEMANDE( C1) 15.00000 0.000000

DEMANDE( ) 17.00000 0.000000

DEMANDE( C3) 22.00000 0.000000

DEMANDE( C4) 12.00000 0.000000

COUT(	E1,		C1)		6.000000			0.000000		COUT(
E1,	)		2.000000		0.000000			COUT(
E1,	C3)		6.000000		0.000000			COUT(
E1,	C4)		7.000000		0.000000			COUT(
E2,	C1)		4.000000		0.000000			COUT(
E2,	)		9.000000		0.000000			COUT(
E2,	C3)		5.000000		0.000000			COUT(
E2,	C4)		3.000000		0.000000			COUT(
E3,	C1)		8.000000		0.000000			COUT(
E3,	)		8.000000		0.000000			COUT(
E3,	C3)		1.000000		0.000000			COUT(
E3,	C4)		5.000000		0.000000			VOLUME(
E1,		C1)		2.000000			0.000000		VOLUME(
E1,		)		17.00000			0.000000		VOLUME(
E1,		C3)		1.000000			0.000000		VOLUME(
E1,		C4)		0.000000			2.000000		VOLUME(
E2,		C1)		13.00000			0.000000		VOLUME(
E2,		)		0.000000			9.000000		VOLUME(
E2,		C3)		0.000000			1.000000		VOLUME(
E2,		C4)		12.00000			0.000000		VOLUME(
E3,		C1)		0.000000			7.000000		VOLUME(
E3,		)		0.000000			11.00000		VOLUME(
E3,		C3)		21.00000			0.000000		VOLUME(
E3,		C4)		0.000000			5.000000

Row Slack or	Surplus	Dual	Price
	OBJ	161.0000	-1.000000		DEM( C1)
0.000000		-6.000000			DEM( )
0.000000		-2.000000			DEM( C3)
0.000000		-6.000000			DEM( C4)
0.000000		-5.000000			SUP( E1)
10.00000		0.000000			SUP( E2)
0.000000		2.000000			SUP( E3)
0.000000		5.000000

Dans cette section nous avons présenté un exemple sous LINGO pour expliquer sa manipulation dans la section suivante nous présentons les résultats obtenus par rapport à notre problématique.

Chapitre 03 : Evaluation de réseau de transport