2.4.2 Formulation du problème
Cette problématique est identifiée par un
certain nombre d'informations des variables de décisions.
les quantités commandées X(j) de
l'entrepôt (j) vers l'unité de production qui est utilisée
pour satisfaire la demande local D(j) en utilisant un nombre fini de moyen de
transport(k) notée N(j, k) qui a une capacité (cap) et un cout de
transport C(j, k).
Au cours de la livraison on est confronté à
plusieurs situations :
> Premier cas
La quantité livrée X(j) est égale à
la demande D(j) ou le centre est en parfait équilibré. >
Deuxième cas
La quantité livrée X(j) est supérieure
à la demande D(j) ou le centre est face à une situation de
sur-stockage avec une quantité Qs(j) en stock ou chaque article
stocké est valorisé par un cout de stockage H (j).
> Troisième cas
La quantité livrée X(j) est inférieure
à la demande D(j) ou le centre est face à une situation de
rupture de stock avec une quantité Qr(j) et un cout de rupture R(j).
Pour régler les problèmes de sur-stockage et la
rupture on ajoute des fourgons K1 qui assure le transite de marchandise Qt(j,
j1, k1)d'un centre vers un autre avec une capacité (cap2) et un
coût (cout).
2.4.3 Les paramètres utilisés
> j : l'ensemble des entrepôts.
> k : l'ensemble des camions.
> Qr1(j) : la quantité des articles en rupture avant
l'approvisionnement. > Qs1(j) : la quantité des articles de
sur-stockage avant l'approvisionnement. > Qr2(j) : la quantité des
articles en rupture après l'approvisionnement. > Qs2(j) : la
quantité des articles de sur-stockage après l'approvisionnement.
> Qt(j ,j1 ,k1): la quantité des articles transportés d'un
entrepôt à un autre.


Chapitre 2 : Présentation de l'entreprise et
formulation du problème
> C (j,k) : le cout de transport de l'usine à
l'entrepôt (j) pas le camion (k).
> N (j,k) : le nombre de camion (k) .
> H (j) : le cout de sur-stockage par article par
période (semaine) .
> k1 : l'ensemble de fourgon.
> Cout : le cout de transport entres les
entrepôts.
> X (j) : la quantité transportée de l'usine
à l'entrepôt (j).
> D (j) : la demande de l'entrepôt (j).
> Cap : la capacité de camion (k).
> Cap1 : la capacité de fourgon (k1).
> R (j) : le cout de rupture par article par
période.
> Pa : prix d'achat.
> Pv : prix de vente.
> Les variables de décision : Qs1(j), Qr1(j),
Qr2(j), Qs2(j), X(j).
2.4.4 Modélisation de problématique
2.4.4.1 Modélisation de problématique
sans fourgon
> La fonction objective
k
Max Z= ? ( D * ( Pv - Pa )) -
( ? ? C* N + ? H * Qs 2 + ? R * Qr
2 )
j j j , k j j j j
|
j
> Les contraintes :
|
j
|
k
|
J j
|
X -? Cap N = V V N ? N +
* , 0 j k j k
, ,
j k j k ,
k
|
X + Qs 1 - Qr 1 - Qs 2 + Qr
2 = D V
j j j j j j
|
j
|
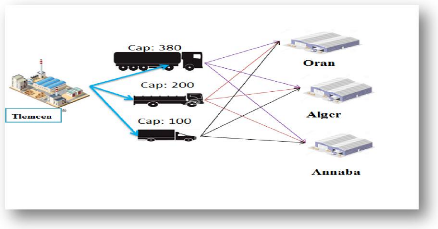
Figure 2.5 : le réseau de distribution de l'entreprise Lit
Mag sans échanges entre les dépôts
Chapitre 2 : Présentation de l'entreprise et formulation
du problème
2.4.4.2 Modélisation de problématique avec
fourgon ? La fonction objective
Max Z =
k
( D * ( Pv - Pa )) - ( C*
N + H* Qs2 + R * Qr2 + Qt
j j J j j j j
*
j,j 1 ,k1
)
Cout
j
?
1
k
J
k
j
j1
j
j
j
? Les contraintes :
X - Cap * N , 0
= V V
j k j k
, , N ? N
j k j k ,
k
+
X + Qs 1 - Qr 1 + Qt Qs 2
Qr 2 Qt D
j j j j 1, j , k 1 - j +
j - = V
j , j 1, k 1 j
j
j1?j j?j1
Qtj , j1 , k1 = Cap k1 V
j V j 1 ? j
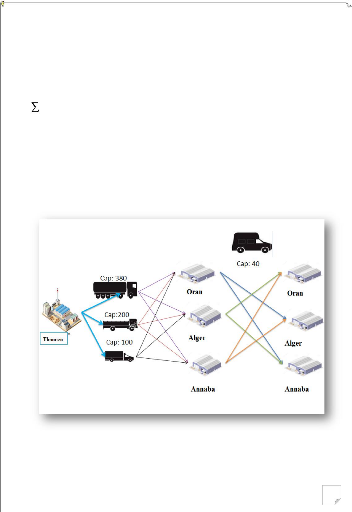
Figure 2.6 : le réseau de distribution de l'entreprise
Lit-Mag avec les échanges entre les
dépôts
| 


