II. Le groupement par 10 et autres groupements
On a vu que le groupement par 10 était essentiel dans
la compréhension de la numération. Dans certaines
expérimentations que j'expliciterai ci-dessous, on remarquera que les
élèves n'arrivent pas souvent au déclic du groupement par
10 (probablement parce qu'ils ne le connaissent pas encore ou parce que le
calcul mental les en empêche ou encore parce qu'il n'y a pas de raison de
grouper par 10, puisqu'il faudrait d'abord avoir compris l'écriture et
la lecture du nombre) mais élaborent d'autres groupements.
En effet, les apprentissages de base de la numération
se font au cycle 2 (à partir du cours préparatoire) mais aussi
dès la maternelle. Les élèves apprennent à compter
jusqu'à 10, jusqu'à 20, jusqu'à 100 etc., mais ne se
rendent pas compte qu'ils abordent déjà le système
conventionnel de la numération consistant à organiser des paquets
de dix (dizaines), puis de dix paquets de dix (centaines) etc.
On peut également remarquer que l'apprentissage de la
numération à l'école se fait de dix en dix (exemple : on
apprend de 0 à 10, puis de 10 à 20 etc.) en utilisant la position
du nombre pour définir sa valeur (système positionnel). Le
système de groupement n'est pas un apprentissage en soi, mais c'est une
méthode qui permet de mieux comprendre et aborder notre système
de numération.
Les principales expérimentations du groupement se font
en poussant les élèves à trouver d'eux-mêmes une
stratégie efficace. Les enseignants cherchent à amener les
élèves à grouper, de façon aléatoire ou
irrégulière pour aller vers le groupement par dix.
Effectivement, c'est grâce à une pédagogie
constructiviste que l'élève, lors d'une situation
problème, va pouvoir renforcer ses connaissances. C'est en cela qu'il
faut les laisser élaborer des stratégies, les laisser
réfléchir ou trouver eux-mêmes la solution, qui ne sera pas
souvent le groupement par 10
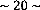
La deuxième expérience de l'article d'Aigoin et
Guebourg (2004) a eu lieu le même jour et consistait en un échange
des rôles entre les deux groupes, c'est-à-dire que le groupe A
devient récepteur du bon de commande que le groupe B aura
élaboré (les élèves du groupe A sont toujours ceux
qui ont une bonne connaissance de la comptine numérique et associe le
mot nombre à son écriture chiffrée et le groupe B sont les
élèves qui connaissent la comptine jusqu'à 30 et
au-delà mais n'associent pas le mot nombre à son écriture
chiffrée).
On peut remarquer que lors de la deuxième
expérience, les élèves du groupe B, qui ont chacun le
même nombre d'éléments à dénombrer, ont fait
des tentatives de stratégies (telles que le marquage des
éléments lorsqu'il est compté par exemple), mais ont tout
de même compris le sens de la communication dans cette situation. Voulant
absolument transmettre leurs messages aux élèves du groupe A, ils
ont fini par grouper de façon irrégulière parfois
(groupements différents : 2/5/6/4) ou de façon
régulière (exemple : groupement par 11).
La stratégie de groupement remplace le
dénombrement terme à terme et permet donc à
l'élève un gain de temps et un apport cognitif pour la suite de
la compréhension de la numération. Les expérimentations
pour amener cette stratégie se font principalement sur de grandes
collections à dénombrer (au-delà de la comptine
numérique qu'ils connaissent) pour que les élèves laissent
de côté le dénombrement unitaire.
Dans cet article (Aigoin & Guebourg, 2004), on peut noter
que le souhait du groupement par dix n'a pas abouti mais cette situation
problème a mis les élèves dans une réflexion
complexe.
Les auteurs ont cherché, grâce à leur
expérimentation, à ce que les élèves créent
une stratégie de groupements irréguliers (exemple : 3/3/4/5) qui
ne seront pas évidents à additionner, afin de les amener aux
groupements par dix (plus simple à appréhender si leurs
capacités en calcul mental le permettent).
Hilli et Ruellan-Le-Coat (2009) nous renseigne sur
l'apprentissage de la régularité des groupements. Les auteurs,
grâce à une expérimentation faite en classe de CP vont
amener les élèves à grouper de façon
irrégulière pour arriver aux groupements par dix.

Lors d'une phase d'institutionnalisation (c'est la phase
où l'on généralise une connaissance) les auteurs disent
que : « pour dénombrer une collection, il n'est pas
nécessaire de compter un à un tous les éléments de
la collection, on peut aussi dénombrer séparément autant
de petits paquets que l'on veut. »
Les groupements sont souvent provoqués par les
enseignants qui choisissent des expérimentations contraignantes pour
obliger les élèves à les utiliser, mais ces derniers n'ont
pas directement l'automatisme de choisir le groupement par 10.
| 


