II. Analyse a posteriori
Séance 1
Lors de la première séance, dix-sept
élèves étaient présents. Une grille d'observation
pour relever les différentes procédures des élèves
a été utilisée. Il a été
précisé aux élèves de faire comme ils souhaitaient
pour dénombrer, y compris utiliser son crayon ; la procédure dite
« sans trace » est celle dans laquelle les élèves n'ont
laissé aucun trait de crayon ou aucune trace écrite :
|
Procédures de dénombrement
|
Nombre d'élèves
|
|
Barrer les billes / mettre un point
|
13
|
|
Faire des paquets
|
0
|
|
Dénombrer sans trace
|
3
|
|
Autres procédures
|
1
|
L'élève ayant utilisé une autre
procédure a écrit la comptine numérique dans chaque bille.
Sa procédure était incorrecte à chaque fois du fait qu'il
ait oublié une bille, ou que la comptine n'était pas correcte.
Lors de l'évaluation, dans le premier exercice de
dénombrement de billes (que
j'appellerai ci-dessous exercice 1), il y avait 28 billes au
total. Dans le deuxième dénombrement (exercice 2), il y en avait
22 et dans le troisième (exercice 3), 36.
'-' 47 '-'
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Dénombrement total de
billes
correct
|
9
|
10
|
4
|
|
Dénombrement total de
billes
incorrect
|
8
|
7
|
13
|
On remarque que les résultats corrects du
dénombrement de billes sont en corrélation avec le nombre de
billes à dénombrer ; plus les nombres sont grands, plus les
élèves ont des difficultés à dénombrer. A ce
niveau, les élèves devaient avoir connaissance de la comptine
numérique jusqu'à 100, mais certains devaient avoir des
lacunes.
C'est parmi tous les dénombrements corrects que nous
allons voir les procédures utilisées par les élèves
:
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Procédure : barrer/pointer
|
9/9
|
9 /10
|
4/4
|
|
Procédure sans trace
|
0/9
|
1/10
|
0/4
|
|
Autres procédures
|
0/9
|
0/10
|
0/4
|
On remarque clairement que les élèves ayant
dénombré correctement sont ceux ayant barrer ou pointer les
billes. On peut imaginer que la procédure la plus experte est bien de
les barrer ou de les pointer afin de laisser une trace qui rend compte des
éléments déjà dénombrés.
Sur les bonnes réponses, seulement trois
élèves ont correctement écrit le nombre de dizaines et
d'unités en fonction de leurs réponses trouvées ; en
effet, même si leurs dénombrements de billes au total
n'étaient pas corrects pour les trois exercices, ils correspondent quand
même à l'écriture du nombre sous la forme dizaines et
unités.
C'est à lors que l'on peut s'apercevoir que les
élèves de cette classe n'ont que très peu de connaissances
par rapport aux groupements décimaux.
Séance 2
Lors de la situation du Grand Ziglotron, dix-neuf
élèves étaient présents et dispersés en neuf
groupes. Cette séance était la présentation de la
situation et ne révèle pas vraiment d'éléments
indispensables à l'appropriation de l'apprentissage du nombre puisqu'il
s'agissait de dénombrer et de coller. Nous pouvons tout de même
nous intéresser aux élèves ayant réussi ou
échoué :
|
6 5 4 3 2 1 0
|
|
|
|
|
Nombre de groupes
|
|
Elèves qui avaient trop de boutons
Eleves qui n'avaient pas assez de boutons
|
Réussite Echec
Lors de cette séance, les procédures les plus
utilisées par les élèves ont été de
dénombrer terme à terme en recomptant plusieurs fois puisqu'ils
étaient par binômes. Les élèves qui ont
échoué n'ont pas tenu compte du fait qu'il fallait demander un
nombre de boutons exact : ni trop, ni pas assez. C'est pour cela que certains
ont redemandé des boutons (chose qui n'a pas été possible)
et d'autres en avaient trop.
Il est important de préciser que lors de cette
séance, les trois marchands désignés ont
réalisé l'activité quand tous les groupes avaient leurs
commandes et je jouais le rôle de la marchande.
Cette séance d'appropriation de l'activité a
été correcte dans le sens ou beaucoup d'erreurs vis-à-vis
des consignes ont été commises ; c'est à ce moment
là que les élèves ont pu se rendre compte des
différentes règles à respecter et qui serviront lors de la
séance suivante.
'-' 49 '-'
Séance 3
Cette séance sera analysée en deux parties :
tout d'abord la situation du Grand Ziglotron, puis l'exercice sur ardoise. Il
est également important de préciser qu'un rappel de la
séance précédente a été fait en début
de séance.
La situation du Grand Ziglotron :
Dans cette situation, nous ne nous intéresserons
évidemment pas au nombre de boutons dénombré par les
élèves (correct ou non), mais au lien qu'ils font entre les deux
écritures des nombres. En effet, ayant rempli le bon de commande
(à cause des contraintes), les élèves devaient donc donner
le nombre de boutons total, le nombre de paquets de dix boutons et le nombre de
boutons isolés.
Parmi les huit groupes d'élèves présents
ce-jour là, nous allons voir combien d'entre eux ont réussi ou
échoué lorsqu'ils ont du écrire le nombre de paquets de
dix et de boutons, si ces nombres ont un lien avec le nombre total de boutons,
mais aussi les procédures qu'ils ont utilisé.
Les nombres de boutons à dénombrer
étaient différents selon trois documents : 28, 34 ou 45
boutons.
Sur les huit groupes :
- Un groupe n'a rien écrit dans les catégories
« paquets de dix boutons » et « boutons ».
- Un groupe a écrit le même nombre pour chaque
catégories (41 boutons, 41 paquets de dix boutons, 41 boutons.).
Ces deux groupes ont probablement manqué de
connaissances par rapport aux paquets de dix boutons et de boutons seuls et se
sont retrouvés en difficultés lors de l'exercice. Les contraintes
ont également été un obstacle pour eux.
- Un groupe a utilisé les mêmes chiffres que
celui du nombre de boutons total mais dans le mauvais ordre : « Il y a 35
boutons. 5 paquets de dix boutons, 3 boutons. ». Les élèves
de ce groupe se sont sûrement rappelé du fait qu'il
s'agissait des mêmes chiffres mais n'ont pas
intégré le sens. Ces élèves n'ont pas
utilisé de stratégie de groupement.
- Deux groupes d'élèves ont groupé par
dix boutons sur leurs Ziglotrons mais n'ont pas su correctement
dénombrer par la suite (exemples : « Il y a 32 boutons, 3 paquets
de dix boutons, 3 boutons », « Il y a 28 boutons, 2 paquets de dix
boutons et 7 boutons ».). Ici, les élèves ont utilisé
une méthode intéressante qui est celle de grouper par dix mais
leurs résultats ne coïncident pas, puisque leurs
dénombrements de paquets de boutons et de boutons n'étaient pas
corrects. Ceci est probablement dû au fait qu'ils n'ont pas fait de lien
entre les deux écritures.
- Enfin, trois groupes d'élèves ont
entouré des paquets de dix sur leurs Ziglotrons et ont correctement
dénombré. En effet, ils ont noté le bon nombre de paquets
de dix boutons et le bon nombre de boutons sauf qu'ils ne sont pas en lien avec
le nombre de boutons total dénombré au départ (Exemple :
le nombre de boutons total à dénombrer est 37 ; sur le bon de
commande il sera écrit 39 boutons ; 3 paquets de dix boutons, 7
boutons). C'est en formant des groupements de dix que les élèves
ont su correctement donner les nombres de paquets de dix et de boutons.
Sur ces huit groupes, cinq groupes d'élèves ont
groupé par dix. Ceci a été amené au fur et à
mesure de la séance par un travail oral avec les élèves
dans lequel ils devaient trouver des stratégies efficaces pour
répondre à l'exercice. Des aides ont été
apportées au cours de la séance puisque les élèves
se sont retrouvés bloqués à cause de la contrainte du
marchand qui ne pouvait pas donner plus de 9 boutons isolés. Une mise en
commun a été faite en demandant aux élèves comment
ils pourraient compter les paquets de dix. Les élèves ont su dire
qu'il fallait faire des paquets de dix. Cela leur a permis de continuer
l'activité sans difficulté supplémentaire.
Dans cet exercice, les contraintes ont posé
énormément de problèmes pour les élèves. Le
fait de ne pas pouvoir demandé un nombre supérieur à 9
boutons isolés les a mis en difficulté dès le
départ. Sans une mise en commun sur la stratégie efficace du
groupement par dix, les élèves se seraient retrouvés
bloqués.
Exercice sur l'ardoise

Après avoir explicité les différentes
stratégies utilisées par les élèves lors de la
situation du Grand Ziglotron, nous avons commencé l'exercice sur
l'ardoise.
Six « calculs » ont été demandé
aux élèves :
- quatre pour le nombre de paquets de dix et de boutons
lorsqu'on leur donne un nombre de boutons total
- deux pour l'inverse
Il a été dit aux élèves que
paquets de dix s'écrivaient « P » sur l'ardoise et boutons
« B ».
Lors du premier calcul, certains élèves ont
formé des paquets de dix avec leurs dix doigts ; par exemple, lorsqu'il
était demandé « 34 », les élèves
tendaient trois fois leurs dix doigts et finissaient par montrer 4 avec une
main. Cette stratégie a été reprise en mise en commun
directe pour faciliter le travail des élèves. En revanche, on
comptait de dix en dix en même temps que l'on montrait nos dix doigts,
pour que les élèves l'intègrent aussi autrement par le
visuel.
La majorité des réponses des
élèves ont été bonnes durant tout l'exercice.
Seulement quelques élèves en difficultés écrivaient
des réponses erronées sur leurs ardoises (exemples : 34 = 4P 3B ;
34P ; 34 B).
L'exercice a bien fonctionné dans la mesure ou
seulement deux élèves avaient des difficultés qui se sont
estompées au fur et à mesure des mises en commun.
C'est à lors que les notions de « dizaines » et
« unités » ont été explicitées.
Séance 4
La séance 4 est une institutionnalisation du sens de la
numération grâce à la situation du Grand Ziglotron. En
effet, les élèves n'ayant qu'à remplir le bon de commande
se sont retrouvé directement face au sens de l'écriture sous
forme dizaine et unité d'un nombre.
Le nombre donné sur le bon de commande était de
42 boutons. Les élèves devaient donc compléter avec 4
plaques de dix boutons et 2 unités.
Sur 19 élèves, 18 ont répondu
correctement à cet exercice. Seul un élève a
répondu « 24 paquets de dix boutons, 14 boutons ».
Les élèves ont très rapidement su
répondre à l'exercice ; en sept minutes tous les
élèves avaient terminé.
Seul un élève s'est servi de la feuille de
brouillon pour y noter : « 10 20 30 40 42 ».
Ces résultats amènent à penser que les
élèves commencent à comprendre le sens de la
numération puisque, sans matériel, ils ont presque tous
répondu correctement. Nous pouvons aussi penser que c'est grâce
à la situation qui commence à être habituelle que les
élèves ont pu répondre correctement. A ce moment de
l'expérimentation, nous ne pouvons pas donner de conclusion.
L'exercice sur l'ardoise est alors repris avec les
élèves.
Ce jour-ci, nous avons fait 14 calculs. En effet, comme la
première situation a été très rapide, nous avons eu
le temps de faire sept nombres à transformer en écriture dizaines
et unités et sept nombres écrits sous forme « dizaine,
unité » à reconstituer.
Les élèves ne devaient plus écrire «
P » pour paquets de dix mais « d » pour dizaines et « u
» pour unités à la place de « B » pour boutons.
Les nombres ont été choisis de façon
à ce que le nombre des dizaines ne soit jamais le même que celui
des unités. Ce choix a été fait pour complexifier la
tâche et pour identifier où apparaitraient les différentes
erreurs des élèves.
|
20 18 16 14 12 10 8 6 4 2 0
|
|
|
|
|
Nombre d'élèves
|
|
FAUX BON
|
24 35 41 46 58 67 73
Voici un histogramme permettant de relever les réponses
des élèves au fur et à mesure des calculs. Les nombres
demandés sont en abscisse.
'-' 53 '-'
On remarque très nettement que la majorité des
élèves ont de bonnes réponses lorsqu'il s'agit de donner
le nombre de dizaines et d'unités. Les quelques mauvaises erreurs sont
faites par des élèves en difficulté ou sont des erreurs
d'inattention des chiffres (exemple : 24 = 24d 0u). Ces erreurs ne sont pas
analysées car on a pu remarqué qu'elles variaient avec les
élèves, c'est-à-dire que ce n'était pas toujours
les mêmes élèves qui faisaient des erreurs de sens, mais
différents élèves qui faisaient des erreurs de confusion.
Nous pouvons penser que les erreurs, plus nombreuses, lors du nombre 73, ont
été causées par le fait que 73 est un grand nombre dont la
sonorité se rapproche de 60 et de 13, ce qui a porté a confusion
chez les élèves.
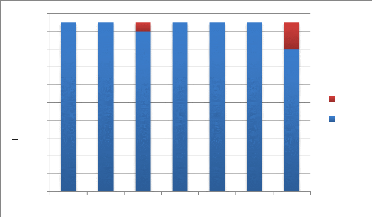
3d 2u 4d 5u 5d 9u 5d 1u 6d 8u 8d 4u 9d 0u
20
18
16
14
Nombre d'élèves
12
FAUX
10
BON
8
6
4
2
0
Voici le graphique des calculs inverses :
On remarque que, demandés sous la forme dizaines et
unités, les calculs sont plus réussis par les
élèves. En effet, ils entendent et voient mentalement les
chiffres demandés de façon directe. Ils peuvent alors
reconstituer le nombre de façon plus simple que lors de calculs
inverses.
Les trois erreurs faites par les élèves lors du
nombre « 9d 0u » ont été dues au fait que les
élèves ne savaient pas comment écrire ce nombre. Le
zéro a porté a
'-' 54 '-'
confusion et il serait intéressant de réutiliser
les nombres « ronds » afin de palier aux difficultés.
Globalement, nous pouvons remarquer que cette séance
représente un tournant dans l'apprentissage de la numération par
les élèves puisque c'est à partir de là qu'ils
commencent à y mettre du sens grâce à des exercices
d'entraînement répétitif et un travail à l'oral
très présent.
Séance 5
La séance 5 reprend l'évaluation de la
première séance. C'est grâce à celle-ci que nous
allons pouvoir repérer les évolutions ou les lacunes persistantes
des élèves.
Il y avait 16 élèves présents.
Nous allons donc reprendre les mêmes données que
lors de la première séance :
|
Procédures de dénombrement
|
Nombre d'élèves
|
|
Barrer les billes / mettre un point
|
6
|
|
Faire des paquets
|
10
|
|
Dénombrer sans trace
|
0
|
|
Autres procédures
|
0
|
On remarque que la majorité des élèves
ont utilisé le groupement. En effet, les groupements comportent dix
billes à chaque fois. Les élèves ont alors
institutionnalisé le fait que pour dénombrer plus facilement et
de manière plus stratégique, il était intéressant
de créer des groupements de dix.
Reprenons désormais le tableau permettant de
vérifier l'échec ou la réussite des élèves
selon les trois exercices :
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Dénombrement total de
billes
correct
|
8
|
13
|
9
|
'-' 55 '-'
|
Dénombrement total de
|
|
|
|
|
8
|
3
|
7
|
|
billes incorrect
|
|
|
|
Grâce à ces résultats, nous pouvons voir
qu'une majorité des élèves ont répondu correctement
lors du dénombrement de billes total pour les exercices 2 et 3 et que la
moitié de ceux-ci ont répondu correctement pour le premier
exercice. Ceci démontre que grâce aux groupements, les
élèves ont éprouvé moins de difficultés
à dénombrer et que, même s'ils n'ont pas groupé, ils
obtiennent des résultats corrects dans la plupart des cas. Ceci est peut
être également dû au fait que les exercices ont
été refaits à plusieurs reprises et que les
élèves n'avaient pas la contrainte de la compréhension
pour réussir.
Nous allons maintenant voir quelles procédures ont
été les plus expertes dans la résolution de ces exercices,
parmi les résultats corrects :
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Procédure :
barrer/pointer
|
4/8
|
5/13
|
5/9
|
|
Faire des
groupements de dix
|
4/8
|
8/13
|
4/9
|
Les résultats restent très mitigés ; il
est vrai qu'entre les élèves ayant barrer ou pointer et les
élèves ayant dénombré, il n'y a pas de
différences notables (sauf pour l'exercice 2 où la
procédure de groupement est privilégiée).
Intéressons-nous maintenant à la partie la plus
intéressante qui est de savoir si les élèves ont
correctement donné l'écriture du nombre sous la forme de dizaines
et d'unités. Nous relèverons les écritures correctes pour
les dénombrements de billes au total qui sont bons, mais
également, pour ceux qui sont faux, puisqu'ils peuvent coïncider
(exemple : si l'élève a dénombrer un nombre faux de billes
au total mais que l'écriture du nombre sous la forme dizaines et
unités est en adéquation avec le nombre de départ, le
résultat est considéré comme bon).
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Ecriture des
dizaines et
unités
correcte
|
10
|
11
|
8
|
|
Ecriture des
dizaines et
unités
incorrecte
|
6
|
5
|
8
|
Il est indispensable de rappeler que lors de la
première évaluation, seuls trois élèves avaient
donné des écritures correctes au moment de donner les dizaines et
les unités.
Lors de cette évaluation, même si les
élèves n'ont pas tous correctement dénombrer les billes,
ils ont quand même, pour la majorité des cas, trouvé des
réponses justes en ce qui concerne l'écriture sous la forme
dizaines et unités. Ils ont fait le lien entre les deux écritures
et ont nettement progressé par rapport aux connaissances de
départ.
| 


