I.4.2.1.1.Plans de Taguchi
Afin d'obtenir des améliorations rapides de la
qualité et des coûts de production, la méthode de Taguchi
vise à combiner un ensemble de techniques. De nombreux statisticiens,
Hunter (1985), Kackar (1985), Box (1988), ont donc essayé de retrouver
dans sa présentation les idées générales de la
statistique sous-jacentes à sa démarche dont les justifications
étaient
Chapitre I Etude bibliographique
21
un peu confuses au départ. La "méthode Taguchi"
vise essentiellement à simplifier la mise en oeuvre des plans
d'expériences.
I.4.2.1.2. Plans de Plackett et Burman (PB)
Ces plans sont quelques fois dits plans de criblage ou
matrices d'Hadamard et se présentent sous forme de matrices
carrées orthogonales dont les éléments sont égaux
à #177;1. Ils sont utilisés dans le but de sélectionner
les facteurs les plus influents sur la réponse Y et où les
interactions sont négligeables ou supposées
négligeables.
I.4.3.2. Plans de modélisation
Il existe plusieurs types de ces plans, parmi les on site :
I.4.3.2.1. Plans de Box-Behnken (BB)
Box et Behnken (1960) ont introduit un type différent
de plans d'expériences pour les modèles du deuxième ordre
qui permettent l'estimation de certaines interactions.
Le modèle Box-Behnken est un modèle factoriel
fractionnaire à trois niveaux développée par Box et
Behnken (Box et Behnken, 1960). Le modèle peut être
considéré comme une combinaison entre un modèle factoriel
à deux niveaux et un modèle à blocs incomplets. Dans
chaque bloc, certain facteurs sont soumis à toutes les combinaisons du
modèle factoriel, tandis que les autres facteurs sont maintenus à
leurs niveaux centraux.
Dans la Figure I.10, le modèle polynomial du second
ordre peut être affiché comme une parcelle de surface ou un
tracé de contours en variant seulement deux niveaux de facteurs, tout en
gardant les autres niveaux de facteur constants.
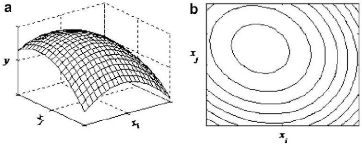
Fig.I.10. a,b (a) : Surface plot, (b) : Contour
plot d'une réponse (Wang and Wan, 2009) Xi : Facteur 1. Xj
: Facteur 2. Y : La répons
| 


