Chapitre 2
par rapport aux coordonnées des noeuds
géométriques de l'élément réel
Vr.
( ) , ( )-* +
De plus les fonctions de transformation sont choisies
identiques pour les trois coordonnées :
( ) < ( )>* +
( ) < ( ) >* +
( ) < ( ) >* +
Par exemple pour un triangle à 3 noeuds xi, xj, xk
:
( ) ( ) ( ) ( ) < ( )> {
( ) ( ) ( ) ( ) < ( )>{
<N > < ( ) ( ) ( )>
Où ( ) appartient à Vr
Les fonctions , sont habituellement des polynômes en
appelées
fonctions de transformation
géométrique.
Elles sont construites de la même manière que les
fonctions d'interpolation N( ).
Grâce à la transformation géométrique
?? nous remplaçons la définition analytique de chaque
élément Ve dans l'espace des x par la
définition analytique, plus simple, de son élément de
référence Vr dans l'espace
Chapitre 2
des . Par la suite nous travaillerons systématiquement
dans l'espace des .
2.5.2. Formes d'éléments de
référence classiques
Nous présentons ci-dessous la forme et la
définition analytique des éléments de
référence correspondant aux éléments classiques [4]
:
Elément de référence à une
dimension :

47 /176
Figure 2.16 : Exemple d'éléments de
référence à une dimension
Elément de référence à deux
dimensions :
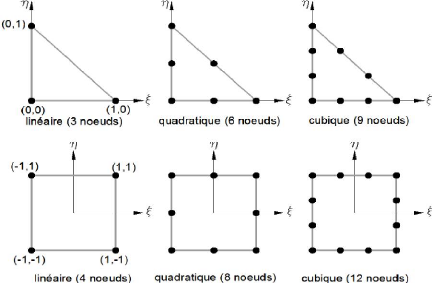
Figure 2.17 : Exemple d'éléments de
référence à deux dimensions
48 /176
| 


