Chapitre 2
Elément de référence à trois
dimensions :
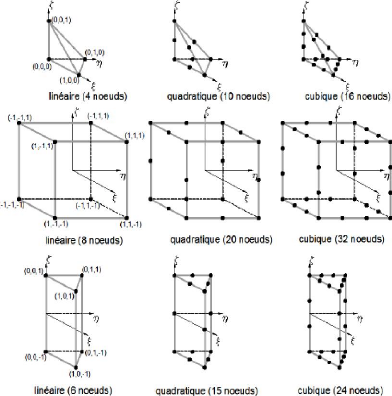
Figure 2.18 : Exemple d'éléments de
référence à trois dimensions
- Dans les éléments de référence
quadratiques, les noeuds situés sur les côtés sont aux
milieux ( ) de ceux-ci. Dans les éléments
cubiques, ils sont situés au tiers (1/3) et aux
deux tiers (2/3) des côtés ;
- Les fonctions de transformation géométrique (
) n'ont pas été données explicitement pour les
éléments de référence ci-dessus. En effet la
construction de ces fonctions est identique à celle des
49 /176
Chapitre 2
fonctions d'interpolation N( ) qui sera
détaillée dans les lignes à suivre.
2.6. Approximation sur un élément de
référence
2.6.1. Expression de la fonction approchée ( )
Nous choisissons sur le domaine V un ensemble de n
noeuds
d'interpolation de coordonnées xi
confondues ou non avec les noeuds
géométriques.
Sur chaque élément Ve nous utilisons une
approximation nodale de la
fonction exacte ( ).
( ) ( ) < ( ) ( ) ( ) > { < ( )>* +
où : x appartient à
Ve,
sont les valeurs de aux e
noeuds d'interpolation de
l'élément, ou variables
nodales,
( ) sont les fonctions d'interpolation sur
l'élément réel.
e ( ) ( ) < ( )>* +
Avec :
( ) , ( )-* +
où : * + sont les variables
nodales de l'élément ;
( ) sont les fonctions d'interpolation sur
l'élément de référence. Remarque :
? En général les fonctions
N(x) ne sont utilisées que pour des
éléments simples. Elles sont le plus souvent remplacées
par les fonctions N( ) où x et sont
liés par la transformation ?? ;
Chapitre 2
? Les mêmes fonctions N( )
peuvent être utilisées pour tous les éléments
possédant le même élément de référence
caractérisé par
:
· sa forme ;
· ses noeuds
géométriques;
· ses noeuds d'interpolation.
2.6.2. Propriétés de la fonction
approchée ( )
2.6.2.1. Propriété fondamentale de
l'approximation nodale
La fonction approchée ( ) coïncide avec la fonction
exacte ( ) en
tous Les noeuds d'interpolation de
l'élément, de coordonnées xi
:
( ) ( ) < ( ) ( ) > {
}
De même, en utilisant l'approximation sur
l'élément de référence
D'où:
Une
( ) ( ) < ( ) ( ) > { }
D'où :
50 /176
( ) {
51 /176
| 


