Chapitre 2
Expression typique de u :
|
|
x appartient
à V
|
|
Approximation
sur le
domaine
|
|
|
|
|
|
|
|
|
|
|
|
Partition en sous-
domaine Ve
x appartient à Ve
Approximation
par sous-
domaines
u( ) < ( )>*á+
Approximation
non nodale
u( ) <N( )>*????+
Approximation
nodale
????( ) <??e( )>*á+
????( ) <????( )>*????+
Approximation
générale
par
sous-domaines
(non nodale
et/ou nodale)
????( ) <????( )>*??????+
Approximation
par éléments
finis
43 /176
Figure 2.13 : Méthodes d'approximation
2.5. Définition de la géométrie
des éléments 2.5.1. Eléments de
référence
De manière à simplifier la définition
analytique des éléments de forme complexe, nous utiliserons la
notion d'élément de référence: un
élément
de référence yr est un
élément de forme très simple, repéré dans
un
espace de référence, qui peut être
transformé en chaque élément réel Ve par
une transformation géométrique [4]. Par exemple dans le cas d'un
triangle:
Chapitre 2
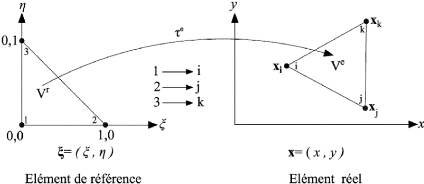
Figure 2.14 : Transformation d'un élément de
référence en élément réel
Afin d'alléger les notations, les
écritures x et seront respectivement
adoptés en lieu et place des notations
classiques (x,y) pour les coordonnées des noeuds dans
l'espace réel et (î,ç) dans
l'espace de référence. La différence pourra se faire
aisément avec l'utilisation de la forme italique
pour les notations classiques.
La transformation ??e définit les coordonnées
x=(x,y) de chaque point de
l'élément réel à partir des
coordonnées =( ) du point correspondant de
l'élément de référence.
La transformation ??e dépend de la forme et de la
position de l'élément réel, donc des coordonnées
des noeuds géométriques qui le définissent. Il y a donc
une transformation ??e différente pour chaque élément
réel :
e e( )
où sont les coordonnées des
noeuds géométriques qui
appartiennent à l'élément e.
44 /176
Elément 1 ( )
45 /176
Chapitre 2
Elément 2 T2: k
x2=x2(,
x1, x5, x3 )
Elément 3 T3: k
x3=x3(,
x5, x4, x3 )
Chaque transformation Te est choisie de manière
à présenter les propriétés suivantes :
ü Elle est bijective en tout point k situé
sur l'élément de référence ou
sur sa frontière : à tout point
Vr correspond donc un point de Ve et un seul, et
inversement ;
ü Les noeuds géométriques de
l'élément de référence correspondent
aux noeuds géométriques de
l'élément réel ;
ü Chaque portion de frontière de
l'élément de référence, définie par
les noeuds géométriques de cette
frontière, correspond à la portion de frontière de
l'élément réel définie par les noeuds
correspondants.
Soulignons qu'un même élément de
référence Vr (par exemple un
triangle à 3 noeuds) se transforme en tous les
éléments réels Ve de même
type (triangles à 3 noeuds) par des transformations Te
différentes :
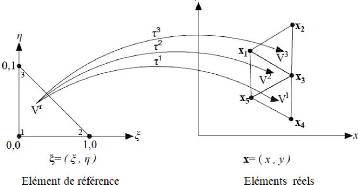
Figure 2.15 : Transformation d'un même
élément de référence en tous les
éléments
réels
Pour simplifier la notation, l'indice supérieur
e, caractéristique d'un
élément, sera supprimé, nous utiliserons une
transformation r linéaire
46 /176
| 


