Chapitre 2
Formulation intégrale Méthodes des résidus
pondérés
Problème d'ingénierie
Hypothèse de
GALERKIN Ö=äu
Formules de Green
(Intégration par partie)
Equations aux dérivées partielles
Conditions aux limites
Formulation intégrale faible
Formulation
intégrale faible
avec
Formulation intégrale forte
Champs de
déplacements
Déformations
Interpolation
Déplacement-Déformations Loi de HOOKE
Vecteurs de localisation
Transformation du système de résolution
Matrice de rigidité et
vecteur force
globaux.
Système [??][????) = [F)
Maillage
Elément de référence Interpolation
Matrice de rigidité et
vecteur force
locaux
expansés
Matrice de rigidité et vecteur force
Déplacements et
réactions aux noeuds
Assemblage
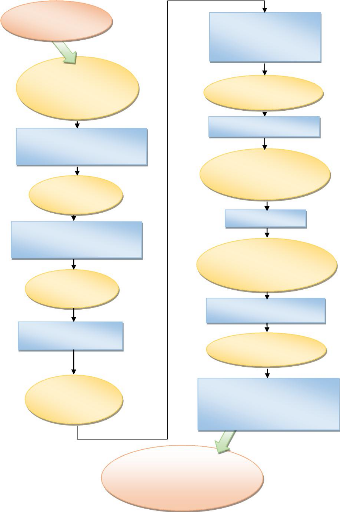
Figure 2.1 : Organigramme descriptif de la démarche de
résolution MEF
Chapitre 2
2.1.2. Principe des éléments finis en calcul
des structures
Partant des hypothèses de petits déplacements et
petites déformations, la mécanique des solides déformable
a permis d'établir deux types d'équations régissant
l'équilibre d'un corps : les équations d'équilibre des
forces et la compatibilité des déplacements.
L'intégration de ces équations n'étant
pas aisée, l'une des méthodes les plus utilisées pour les
résoudre est celle dite des éléments finis
qui revient à remplacer le système continu
par un système discret.
Le solide est alors divisé en un certain nombre de
sous-domaines dont l'assemblage permet la
reconstitution de la géométrie initiale.
Le processus de division du solide en un ensemble de
sous-domaine s'appelle le maillage, on parle également
de discrétisation géométrique du
solide.
Chacun de ces sous-domaines porte le nom
d'éléments et ces éléments
sont dits finis parce qu'ils sont de forme
et de dimension connue. Ils sont reliés entre
eux par des noeuds dont les degrés de
liberté (DDL) constituent les inconnues du problème.
31 /176
Figure 2.2 : (a) - Solide (Poutre en I) ; (b) Modèle
éléments finis
Considérant un champ de déplacement
cinématiquement admissible sur l'élément, la
méthode consiste le plus souvent à approximer
celui-ci au moyen d'une fonction polynomiale formée d'un nombre
fini de paramètres et à l'exprimer en fonction des
déplacements nodaux (les
32 /176
| 


