Chapitre 2
déplacements associés aux degrés de
liberté), on aboutit à une approximation nodale
du champ de déplacement.
Les principales étapes de construction d'un
modèle éléments finis sont les suivantes [24]:
y' Discrétisation du milieu continu en
sous-domaines (maillage) ;
y' Construction de l'approximation nodale par
sous-
domaine (approximation par éléments
finis) ; y' Calcul des matrices élémentaires
correspondant à la forme
intégrale du problème ;
y' Assemblage des matrices
élémentaires - Prise en compte des conditions aux limites
;
y' Résolution du système
d'équations.
La résolution du problème nécessite alors
une profonde maitrise :
y' des règles de maillage ;
y' du principe de construction de l'approximation nodale ;
y' du processus de calcul des matrices élémentaires
;
y' et de la notion d'assemblage.
Nous expliciterons chacune de ses étapes dans la suite.
2.2. Discrétisation géométrique
(maillage) 2.2.1. Définition du maillage
Un maillage est la discrétisation
spatiale d'un milieu continu, ou aussi, une modélisation
géométrique d'un domaine par des éléments
proportionnés finis et bien définis. L'objet d'un maillage est de
procéder à une simplification d'un
système par un modèle représentant ce système et,
éventuellement, son environnement (le milieu), dans l'optique de
simulations de calculs ou de représentations graphiques.
On parle également dans le langage commun de
pavage du domaine. Un maillage est défini par [19] :
y' son repère ;
Chapitre 2
? les points (noeuds) le constituant,
caractérisés par leurs coordonnées ;
? les cellules (éléments finis)
reliant n de ces points ;

Figure 2.3 : Maillage d'un pont de type Bow-string en vue d'une
simulation
2.2.2. Caractérisation d'un maillage
Un maillage se caractérise par [19] :
- sa dimension : typiquement 1D, 2D ou 3D ;
33 /176
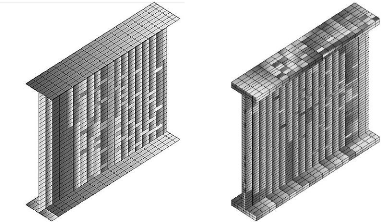
Figure 2.4 : (a) maillage en 2D (poutre I) ; (b) maillage en 3D
(poutre I)
34 /176
| 


