CHAPITRE 4. MÉTHODOLOGIE ET
IMPLÉMENTATION
spéciation 2, création 3,
et perte 4 de protéines. La figure 4.1 montre un exemple
d'arbre d'évolution d'un ensemble de protéines. On observe qu'il
y a deux créations et trois pertes de protéines dans cet
arbre.
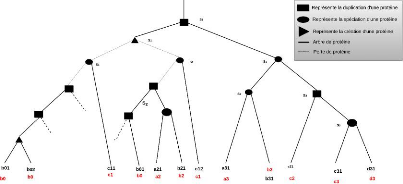
FIGURE 4.1 - Arbre de protéines étiqueté
avec les événements de spéciation, duplication,
création et perte
4.1.2 Définitions formelles
Dans cette section, 8 représente, l'ensemble des
espèces, g représente l'ensemble des gènes d'une famille
de gènes et P représente l'ensemble de protéines produites
par les gènes d'une famille. On définit sur ces ensembles des
fonctions de correspondance : s : g - 8 qui à tout gène
fait correspondre l'espèce à laquelle il appartient et g :
P - g qui à toute protéine fait correspondre le gène
qui l'a produit. Les trois ensembles 8, g et P sont tels que 8 =
{s(x) : x E g} et g = {g(x) : x E P}, c'est
à dire que les fonctions s et g sont surjectives.
Arbres phylogénétiques : Tous
les arbres phylogénétiques considérés sont
enracinés et binaires. Un arbre T pour un ensemble L
est un arbre binaire enraciné dont l'ensemble des feuilles est
L. L'ensemble des feuilles d'un arbre T est notée
G(T)
2. Spéciation : une protéine a donné
naissance à deux protéines par le biais d'une spéciation
d'espèce.
3. Création : une protéine est apparue à
un certain moment dans un gène
4. Perte : un gène a perdu la fonctionnalité de
produire une protéine à un certain moment
27
| 


