3.3.3) Interprétation des résultats et tests
d'hypothèses jointes
La statistique du t empirique lié au coefficient
ö=-1,78 est supérieure à la valeur lue dans la table
à 1% (=-4,06), dans ce cas, on retient l'hypothèse nulle
d'existence d'une racine unitaire, la série n'est pas stationnaire.
Selon la stratégie des test de D&F, après le test de
recherche du racine unitaire on doit effectuer les tests d'hypothèses
jointes.
L'hypothèse jointe consiste à tester la
nullité du coefficient de la tendance conjointement à la
nullité de ö,  , pour tester l'hypothèse  on doit calculer la statistiques suivante :
 où :
 est la somme des carrés des résidus du modèle 6
contraint par  .
La statistique  est analogue à la loi de Fisher, les seuils critiques de cette
statistique sont tabulés par D&F.
Pour une taille d'échantillon de 100 observations
(T=100) pour le modèle 3 contenant la constante et la tendance, la
valeur critique de F tabulée par D&F est 6,49, on a alors,  , dans ce cas on retient  .
En poursuivant toujours le schéma de la
stratégie de D&F, on doit tester une autre hypothèse jointe
en cas d'acceptation de l'hypothèse jointe  , cette hypothèse consiste à tester la nullité
simultanée des coefficients  .
 .
Pour discriminer entre l'hypothèse 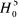 et l'hypothèse alternative, on va utiliser une statistiques F,
elle aussi analogue à loi de Fisher, dont les valeurs sont
tabulées par D&F.
La valeur critique de Fuller à 5% pour un
échantillon de taille 100 du test F pour le modèle 6 contenant la
tendance et la constante est 6,49, dans ce cas on a  , dans ce cas on accepte  de la nullité des coefficient c, b et ö.
La stratégie des tests de D&F nous emmène
à l'estimation des paramètres du modèle 5 en cas
d'acceptation de l'hypothèse  , le modèle 5 de par sa construction ne contient pas la tendance
mais par contre il contient la constante, il s'écrit comme suit :
 .
Estimation du modèle 5 et test de racine unitaire
:
|
Null Hypothesis: PAX_ADJ has a unit root
|
|
|
Exogenous: Constant
|
|
|
|
Lag Length: 3 (Automatic based on SIC, MAXLAG=6)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-1.320082
|
0.6175
|
|
Test critical values:
|
1% level
|
|
-3.503049
|
|
|
5% level
|
|
-2.893230
|
|
|
10% level
|
|
-2.583740
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(PAX_ADJ)
|
|
|
Method: Least Squares
|
|
|
|
Date: 02/28/13 Time: 15:15
|
|
|
|
Sample (adjusted): 2005M05 2012M12
|
|
|
Included observations: 92 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
PAX_ADJ(-1)
|
-0.050461
|
0.038226
|
-1.320082
|
0.1903
|
|
D(PAX_ADJ(-1))
|
-0.816838
|
0.104092
|
-7.847245
|
0.0000
|
|
D(PAX_ADJ(-2))
|
-0.632572
|
0.118706
|
-5.328918
|
0.0000
|
|
D(PAX_ADJ(-3))
|
-0.347751
|
0.102258
|
-3.400722
|
0.0010
|
|
C
|
33600.81
|
19599.07
|
1.714409
|
0.0900
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.455333
|
Mean dependent var
|
2510.240
|
|
Adjusted R-squared
|
0.430291
|
S.D. dependent var
|
40584.28
|
|
S.E. of regression
|
30632.64
|
Akaike info criterion
|
23.55034
|
|
Sum squared resid
|
8.16E+10
|
Schwarz criterion
|
23.68739
|
|
Log likelihood
|
-1078.315
|
F-statistic
|
18.18264
|
|
Durbin-Watson stat
|
2.111856
|
Prob(F-statistic)
|
0.000000
|
|
|
|
|
|
|
|
|
|
|
L'application du test D&F augmenté sur le
modèle 5 contenant la constante montre la présence d'une racine
unitaire de la série Pax-adj, en effet, la statistique
tö de la variable endogène retardée Pax-adj(-1)
=-1,32, cette valeur est à comparer avec la valeur des seuils de D&F
pour le deuxième modèle. Au seuil de 5%, on a  , selon l'estimation du modèle 5, la  , on alors  dans ce cas on accepte l'hypothèse nulle de la présence
d'une racine unitaire (ö=0).
L'acceptation de la présence d'une racine unitaire au
niveau du modèle 5 nous emmène à tester l'hypothèse
jointe  , cette hypothèse suppose la nullité de ö
conjointement à la nullité de la constante ;  contre l'hypothèse alternative  au moins un des éléments est différent.
La valeur de la statistique  , cette valeur est à comparer avec les valeurs de la distribution
théorique de ö pour le modèle 5 au niveau de la table IV de
D&F, pour une taille d'échantillon de 100 observations et pour un
risque d'erreur de 5%, la valeur limite est 4,71, ainsi on a  dans ce cas on accepte l'hypothèse nulle 
Après le test de l'hypothèse , il faut tester la nullité de la moyenne  de la série.
|
Hypothesis Testing for PAX_ADJ
|
|
|
Date: 03/04/13 Time: 15:39
|
|
|
Sample: 2005M01 2012M12
|
|
|
Included observations: 96
|
|
|
Test of Hypothesis: Mean = 0.000000
|
|
|
|
|
|
|
|
|
|
|
Sample Mean = 504795.9
|
|
|
Sample Std. Dev. = 89724.46
|
|
|
|
|
|
|
Method
|
Value
|
Probability
|
|
t-statistic
|
55.12398
|
0.0000
|
|
|
|
|
|
|
|
|
La moyenne de la série est largement et
significativement différent de 0. Le processus générateur
de la série est une marche au hasard sans dérive.
| 
