La gestion des risques dans le cadre des assurances- vie. Cas de la compagnie TRUST Assurances de Personnes (Alger )

6.2 Etude de l'assurance groupe de Wataniya Telecom Algérie

De même, nous estimons préalablement les paramètres de la distribution nécessaires au test (K-S), à savoir la moyenne et l'écart-type et nous utiliserons SPSS? test non paramétrique? test de (K-S). Les observations représentent l'âge des assurés de la Wataniya Télécom Algérie, comparé à la répartition théorique d'une loi normale (á=0,05).

Table 29 Paramètres estimés de la distribution des assurés de Wataniya Télécom Algérie

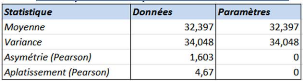
a.1 Statistiques estimées paramètres de la loi Normale

Table 30 Statistiques estimées à partir des données Wataniya Télécom Algérie et calculées à partir des estimateurs des paramètres de la loi Normale

94

Chapitre III : Elaboration et étude du cas Trust Algérie

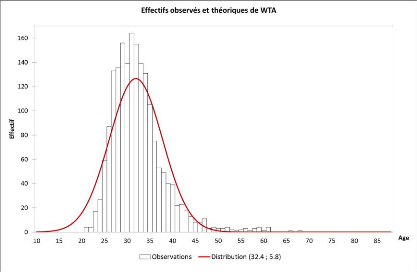
Figure 20 Effectif observés et théorique des assurés de Wataniya Telecom Algérie

Figure 21 Histogramme de densité et fonction de répartition des fréquences cumulés des assurés de la Wataniya Telecom Algérie

a.2 Test de Kolmogorov-Smirnov

Table 31 Test de Kolmogorov-Smirnov de sur la distribution de Wataniya Telecom Algérie pour une loi Normale

95

Chapitre III : Elaboration et étude du cas Trust Algérie

a.3 Interprétation du test de K-S

> Hypothèse nulle _(H0), l'échantillon suit une loi Normale

> Hypothèse alternative (H1), l'échantillon ne suit pas une loi Normale

Etant donné que la valeur de signification asymptotique bilatérale est inférieure au niveau de signification (á=0,05), on doit retenir l'hypothèse nulle (H0) et rejeter l'hypothèse alternative (H1).

Nous pouvons donc conclure que la distribution testée suit une loi gaussienne de paramètre (32,39 ; 5,83)

6.3 Mesurer et comparer le risque

L'estimation ci-dessus nous renseigne sur les distributions des âges pour chaque assurance groupe, mais ne permet toujours pas de mesurer le risque affecté. En effet, même si nous connaissons cette distribution, nous devons y affecter une probabilité de décès (d_x), lui correspondant.

Pour cela, nous utiliserons le modèle Makeham étudié précédemment (voir Figure 8 Régression non linéaire des dx (modèle Makeham) page 74), afin d'établir une fonction de risque pour chaque portefeuille de contrat, qui représente le produit de la distribution des assurés par âge, par la probabilité de décès (d_x).

Pour mesurer le risque du contrat groupe Société Générale, nous utiliserons les âges représentés par une loi gaussienne de paramètres N-'(47,04 ; 9,42) pondéré par leurs probabilités. Il en est de même pour Wataniya Telecom Algérie représenté par la loi gaussienne de paramètre N-'(32,39 ; 5,83).

	Wta	SG
i de x	32,40	47,05
o de x	5,84	9,43		i de qx
2,60E-05	7,74E-05	o de qx
4,51E-05	9,64E-05
qx^(1)	2,01E-03	5,56E-03

qx ⁽¹⁾ la probabilité de décès correspondant à la moyenne d'âge pour les deux distributions respectivement (2,01^E-03) pour un âge x=32,4 et (5,56^E-03) pour l'âge x=47,05. Nous pouvons constater que l'assurance groupe de la Société Générale représente un risque plus important que celui de Wataniya Telecom Algérie. Cependant on ne peut se contenter de cette estimation du risque, du fait que la distribution n'est pas équiprobable, les probabilités qui y sont affectées suivant une loi de type exponentielle (Gompertz Makeham).

Avant de calculer la moyenne du risque pour chaque contrat assurance groupe, nous devons pondérer les deux distributions avec les probabilités correspondantes. Ce n'est que

96

Chapitre III : Elaboration et étude du cas Trust Algérie

par la suite que nous calculerons la moyenne pour obtenir les résultats suivants u (q_x) de WTA égale 2,60^E-05, celui de SG correspond à 7,74^E-05. Cela conforte la première estimation toute en relevant que le risque pour chaque portefeuille de contrat est inferieur à notre première estimation qui prenait en compte uniquement la probabilité correspondante à la moyenne de la distribution u (qx) de chaque contrat groupe ; cette dernière sera utile pour pouvoir établir une prime correspondante.

Aussi, après avoir étudié et comparé les moyennes de chaque distribution, nous devons nous tourner vers l'étude de la variance, tout en sachant que plus une distribution est étendue, plus le risque d'avoir des évènements qui seront éloignés de l'estimation de la moyenne, augmentera.

En outre, nous avons aussi pu constater que la structure de la population assurée diffère de la population générale.

Cela doit nécessairement être pris en considération par l'assureur lors de l'établissement du contrat et de la prime d'assurance. En effet, cette différence de structure crée inexorablement une différence de paramètre, et une prime groupe qui sera calculée en conséquence. Aussi nous constatons une différence entre la moyenne (qx) de la population assurée et celle de la population générale ajustée par le modèle de Gompertz Makeham (voir Table 8 page 77).

Nous pouvons alors noter que la moyenne q_x (probabilité de décès) pour les différents contrats assurance groupe, à savoir la moyenne pour WTA et la SG respectivement u(q_x) =2.60^E-05 et u(q_x)=7.74^E-05, est nettement inférieure à la moyenne u(q_x)=0,08228 de la population générale.

Ces informations relatives à la composition de la population pour chaque contrat groupe, nous permettent de pouvoir établir une tarification adéquate. Cependant, dans la pratique il arrive que ces informations ne soient pas toujours disponibles. Aussi en l'absence d'informations détaillées, l'actuaire pourra employer l'âge moyen arithmétique du groupe qu'il majorera de 4 à 8 ans en fonction des capitaux garantis, et établir une tarification globale, en se basant sur l'âge moyen actuariel (Bakayoko 2007).

97