6 Comparaison de deux assurances groupes
Pour bien appréhender le risque lié à
l'assurance groupe, nous allons comparer deux assurances groupe (voir page11).
Ces échantillons vont nous permettre, dans un premier temps, de voir la
composition du portefeuille des assurés, et à travers ceci de
voir les étapes nécessaire à l'estimation du risque d'un
portefeuille de contrats. Pour ce faire nous comparons le portefeuille de
contrat de Wataniya Telecom Algérie composé de 1855
assurés, et celui de Société Générale
composé de 9099 assurés.
La première étape consiste à calculer
l'âge de chaque assuré pour l'année 2011 et de calculer
dans une deuxième étape, les fréquences pour chaque
âge.
6.1 Etude de l'assurance groupe de la
Société Générale
D'après l'histogramme de distribution des effectifs,
nous pouvons poser l'hypothèse que la distribution de l'effectif suit
une loi normale. A cet effet, nous utilisons dans XLstat dans
modélisation des données, l'ajustement d'une loi de
probabilité.
a) Paramètres estimés des
assurés de la Société
Générale

Table 26 Paramètres estimés de la
distribution des assurés de la Société
Générale
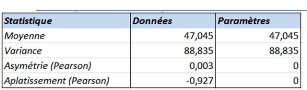
a.1 Statistiques estimées des paramètres de
la loi Normale
Table 27 Statistiques estimées à
partir des données Société Générale et
calculées à partir des estimateurs des paramètres de la
loi Normale
Le test non paramétrique de Kolmogorov-Smirnov (K-S),
consiste à mesurer l'écart maximum qui existe entre la fonction
de densité cumulée observée (ou tout simplement les
fréquences cumulées), et la fonction de répartition
théorique qui nécessite l'utilisation de la table de Kolmogorov.
Sous l'hypothèse nulle (H0), cet écart est faible et la
répartition des observations s'intègre dans une distribution
théorique.
Dans notre cas, les observations représentent
l'âge des assurés de la Société
Générale, comparé à la répartition
théorique de la loi normale pour (á=0,05). Nous
avons préalablement estimé les paramètres
nécessaires au test (K-S), à savoir la moyenne (47,04), et
l'écart-type (9,42). (Il y a lieu de signaler que le test de (K-S) a
été effectué avec SPSS? test non
paramétrique).
Chapitre III : Elaboration et étude du cas Trust
Algérie
a.2 Test de Kolmogorov-Smirnov

Table 28 Test de Kolmogorov-Smirnov de sur la
distribution de la Société Générale pour une loi
Normale
a.3 Interprétation du test de K-S
> Hypothèse nulle (H0), l'échantillon
suit une loi Normale
> Hypothèse alternative (H1), l'échantillon ne
suit pas une loi Normale
Etant donné que la valeur de signification asymptotique
bilatérale est inférieure au niveau de signification
(á=0,05), on doit retenir l'hypothèse nulle (H0)
et rejeter l'hypothèse alternative (H1).
Nous pouvons donc conclure que la distribution testée suit
une loi gaussienne de paramètre (47,04 ; 9,42) pour
(á=0,05)
L'âge moyen arithmétique du groupe
dénommé âge moyen actuariel du groupe, sera d'une grande
utilité, pour établir une tarification adéquate.
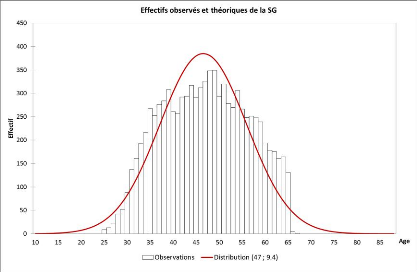
92
Figure 18 Effectif observés et
théorique des assurés de la Société
Général
93
Chapitre III : Elaboration et étude du cas Trust
Algérie

Figure 19 Histogramme de densité et
fonction de répartition des fréquences cumulés des
assurés de la Société
Générale
| 


