III.2.2.2.1 Introduction : [39]
La méthode des Ensembles de Niveau Zéro
est une méthode de simulation numérique utilisée pour
l'évolution des courbes et des surfaces dans les domaines discrets .
Cette méthode permet de faire évoluer une courbe
paramétrique fermée C(p) suivant une équation du type
=FN
(III.16)
Où t est le temps, F
est la vitesse d'évolution et N est la normale unitaire
à la courbe.
Chaque point de la courbe C évalue
suivant la direction normale à la courbe avec
Une vitesse F.
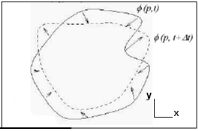
L'avantage principal de cette méthode est la
possibilité de gérer automatiquement le changement de topologie
de la courbe en évolution. La courbe C peut être divisée en
deux ou trois courbes, Inversement plusieurs courbes peuvent fusionner et
devenir une seule courbe. La méthode des Ensembles de Niveau Zéro
est capable de réaliser ce changement en utilisant une fonction d'ordre
supérieure.
Pour une courbe plane C(p), un tableau bidimensionnel de
nombres réels ö(x,y) est utilisé pour sa
représentation. L'évolution de la courbe signifie la mise
à jour de tout le tableau ö(x,y).
D'abord nous initialisons (en ö(x,y)) à
zéro les pixels correspondants au passage de la courbe C, après
il faut calculer pour le reste des éléments du tableau, la
distance euclidienne à la courbe C, qui sera négative à
l'intérieur et positive à l'extérieur. Autrement dit, le
tableau bidimensionnel ö sera rempli de la manière suivante :
zéro tout le long de la courbe C, et la valeur de la distance
euclidienne au point le plus proche de la courbe pour tout le reste. S'il
s'agit d'un élément à l'intérieur de la courbe C
(c'est une courbe fermée) le signe de son contenu sera
négatif.
III.2.2.2.2 Principe d'évolution de la courbe
C: [39]
Etant donné Ù une sous ensemble
borné de R2, avec ??Ù en tant que sa frontière.
Puis une image de deux dimensions U0 on peut la définie comme
U0 : Ù -->R. dans ce cas Ù n'est qu'un
rectangle grillé fixe. Maintenant on considérer
l'évolution de la courbe C dans Ù, comme le frontière d'un
sous ensemble ouvert w de Ù. En d'autres ; w c Ù, et C est
le frontière c de w(C=??w).
L'idée principale est d'enfoncer la propagation de la
courbe comme une fonction de dimension supérieure d'ensemble du niveau
zero. on définir la fonction comme suit :
Où d est la forme de distance (x,y) à ??w dans
t=0, et le signe plus ou moins est choisir si le point (x,y) es t à
l'extérieure ou à l'intérieur de la sous ensemble w .
Maintenant l'objectif est d'introduire une équation
pour l'évolution de la courbe .
La courbe évoluer dans la direction de sa normale
suivant l'équation dérivée partial suivant
,
Ou l'ensemble {(x,y)} définir le contour initial, et F
la vitesse de propagation. Pour certin forme de la vitesse F, ceci est
réduit à l'équation standard de Hamilton-Jacobi. Il y a
plusieur avantages principaux à cette formulation. Le premier est que
Ø(x,y,t) raste toujours une fonction tant que F est lisse. Quand la
surface Q est évoluée, la courbe C peut se divisée en
plusieurs courbes, se fusionnée en un seul et changer la topologie.
Un autre avantage est que des propriétés
géométriques de la courbe sont facilement
déterminées à partir d'un ensemble de niveau particulier
de la surface Q. Par exemple, le vecteur de la normal pour chaque point de la
courbe est donné par :
N=
(III.17)
Et la courbure K est obtenue à partir de la divergence
du gradient du vecteur normal d'unité au front :
K=div=
(III.18)
En fin, un autre avantage est que nous pouvons
évoluée des courbes dans les dimensions supérieures
à deux la formulation précédente peut être
facilement généralisé pour des dimensions
élevées. C'est utile en propageant une courbe pour segmenter des
données de volume.
a. Contour active avec un
« arrêt-au-bord » : [39]
Le but maintenant est de définir une fonction
de vitesse F à partir des données de l'image. Malladi et al.
Accomplissent ceci en divisons d'abord F dans deux composants :
F=FA+FG.
FA représente un terme constant d'advection
qui forcera la courbe pour s'étendre ou se contracter
uniformément basé sur son signe. Ceci agit comme la force
d'inflation utilisée dans les modèles traditionnels de
« serpents ». Le deuxième terme FG
dépend de la géométrie de la courbe et agit pour
lisser les régions de grande courbure.
Cependant , nous avant besoin également d'une
méthode pour arrêter l'évolution de la courbe à la
frontière de l'objet. Si on suppose que les frontières sont
définies par le gradient de notre image U0, nous pouvons
créer une fonction « d'arret-au-bord » g :
g(u0)=,p1
(III.19)
Ou G0(x ; y)*U0(x, y) est
simplement la convolution de U0 .
La fonction g(U0) a des valeurs proches de ZERO
(0) dans les régions ou le gradient de l'image est élevé,
et desvaleurs proches de UN(1) dans des régions homogènes.
Une autre fonction « d'arret-au-bord » qui
tend plus rapidement vers zéro sur les frontières peut etre
définie comme siut :
g(u0)=
multiplier notre fonction de vitesse F par cette fonction
« d'arret-au-bord » g. On applique les changements
ci-dessus, alors l'équation 2 peut etre récrit comme suite :
=g(u0)(FA+
FG).(x,y ,0)=(x,y )
Maintenant pour discrétiser , on utilise l'approche des
différences finies. Soit l'étape de temps et (xi,
yj) les poits de grille pour1.j .Et on prend=(,nune approximation de
avec n0, . Les différences finies sont décrites par la notation
suivante :
=-. -
=-. - -
(III.20)
Malladi et Al utilise un terme constante d'advection
FA=1 et utilise des approches introduite par sethian et al pour
estimes
FA :=1/2
(III.21).
La force restante fG est basée
sur la courbure K(Equation3).Malladi et al. Multiplier cette force par une
restante négatif très petite å et prend une approximation
de | Ø|,on utilisant des défférences centrales.Donc une
estimation de FG | Ø| est :
FG=-- cK
(III.22)
Alors pour faire évoluer, on résolue la
discrétisation suivant de équation (6) :
(III.23)
b. Contour active sans arrêt aux
bords : [17]
Rappelant que la courbe C peut etre considérer comme
étant la frontière d'une sous ensemble ouvert de Ù
(c'est-à-direC=w). Notons la région par intérieur (C) et
la région Ù\par extérieur(C). Au lieu de fonder le
modèle sur une fonction « d'arret-au-bord » nous
allons interrompu l'évolution de la courbe par l'intermédiaire de
l'approche de minimisation d'énergie.
Considérons le cas simple d'une image u0
formé par deux régions d'intensité constante par morceau.
Notons les valeurs de l'intensité par et. En plus supposans que l'objet
à détecté a une région de bord C0 et
d'intensité. Par suit intérieur (C0),
l'intensité de u0est approximativement, alors que pour
extérieur (c0), l'intensité de u0 est
approximativement . Puis on considèrent un terme d'ajustement .
F1(C)+F2(C)=
Nous pouvons dire que l'on est sur les bords de l'objet
quand
En effet, si la courbe est à l'intérieur de
l'objet :
Si elle est à
l'extérieur :
Si elle est sur le bord
: :
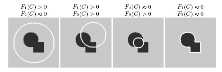
On obtient donc une énergie F en fonction de C, c1 et
c2 telle que :
F(C, c1, c2)=longueur(C)+v.superficie(C) +
+
Avec , , ,sont des paramètres positifs.
Longueur (c) est un paramètre de lissage de la
courbe.
la méthode du LevelSet est utilisé pour faire
évoluer la courbe C. Cette méthode permet de propager une courbe
qui est représentée par lorsque est égal à 0.
Pour cela, on crée une nouvelle image de même
taille que l'image I que l'on veut traiter. Dans cette image, on a la courbe C
pour =0, on est à l'intérieur de la courbe pour >0, et
à l'extérieur pour <0. On initialise alors
indépendamment de I. On calcule alors la distance signée
.c'est-à-dire en partant d'une image dont la valeur est -1 à
l'extérieur et + 1 à l'intérieur et on cherche à
avoir une valeur qui tend vers 0 au bord, qui croît vers
l'intérieur et qui décroît vers l'extérieur. La
distance signée est donnée par l'équation suivante .Pour
le cas continu.

(III.24)
Pour le cas en discret :
(III.25)
Avec :
En revenant à l'image I, on a alors une nouvelle
fonction
(C, c1, c2)=longueur ()+v.superficie() +
+
On définit alors la fonction Heaviside H :
(III.26)
La fonction Dirac est définie par
(III.27)
On exprime les termes de l'énergie F de la
manière suivante :
L'expression de l'énergie peut alors s'écrire de
la forme suivante :
En gardant Ø fixé, et en minimisant
l'énergie F selon c1 et c2, on peut facilement exprimer ces constantes
c1 et c2 en fonction de Ø :
(III.28)
En gardant alors c1 et c2 fixés, on minimise
l'énergie selon Ø pour obtenir l'équation de
Euler-Lagrange pour Ø:
où div est la courbure [3] qui permet de garder une
courbe lisse.
En discret, l'équation d'évolution est de la
forme :
Avec :
K=div=
ET.
est la vitesse d'évolution.
Pour les images multi spectrales, le principe reste le
même, il suffit juste de considérer ces images comme plusieurs
images mono spectrales. On obtient alors pour les moyennes:
et on obtient pour l'évolution de
(III.29).
| 


