III.2.2.1 La méthode de détection par
Snake : [02]
III.2.2.1.1 Principe de base de la
méthode :
La méthode de détection par Snake, ou
contour actif, consiste à placer aux alentours de la forme à
détecter une ligne initiale de contour. Cette ligne va
se déformer progressivement selon l'action de plusieurs forces qui vont
la tirer ou la pousser vers la forme.
Les forces impliquées vont dériver de (3)
énergies associées au Snake:
· Une énergie propre, due uniquement à la
forme du contour, dite énergie interne: E
int.
· Une énergie potentielle imposée par
l'image: E image. C'est elle qui va attirer la
ligne du snake vers les contours réels présents sur l'image.
· Une énergie E cont
qui exprime certaines contraintes supplémentaires qui peuvent être
imposées par l'utilisateur vu le Snake qu'il veut obtenir
a. L'énergie interne
Elle va dépendre uniquement de la forme du Snake. C'est
une contrainte de régularité sur la courbe. Elle s'écrit:
E int = (a(s)).||(Vs(s)||2 +
b(s)).||(Vss(s)||2)
(III.12)
a et b sont les poids respectifs accordés à la
dérivée première Vs et à la dérivée
seconde Vss. On ajustera a et b pour trouver un intermédiaire entre un
contour souple mais pas forcement très régulier (et qui pourra
alors se caler sur des coins et des angles aigus) et un contour très
régulier qui suivra bien le contour sans s'accrocher sur des petites
aspérités.
b. L'énergie potentielle liée à
l'image :
Elle caractérise les éléments vers
lesquels on veut attirer le Snake sur l'image. Pour notre problème,
puisqu'il s'agit de détecter des contours, on va s'intéresser aux
lignes de fort gradient:
E
image= -gradient(i)
(III.13)
Pour certains problèmes, on peut choisir d'attirer le
Snake vers des zones présentant d'autres caractéristiques: vers
les zones les plus sombres par exemple.
c. L'énergie de "contrainte".
Elle est définie par l'utilisateur selon les
spécificités du problème. On peut par exemple imposer une
distance minimale ou maximale entre deux points consécutifs du contour
actif. Elle va s'exprimer en fonction de V(s) uniquement:
E cont=E cont(s)
(III.14)
d. Energie totale du contour actif :
[16]
L'énergie totale en un point du Snake V(s) va donc
s'écrire:
E totale(V(s), Vs(s), Vss(s)) = E int(V,
Vs, Vss) + E image(V) + E cont(V).
Nous avons affaire à un nombre de points Vi fini. On
exprime directement Ei: énergie au point Vi en fonction de tous les
points V du Snake en utilisant notamment:
Vis(s)= Vi - Vi-1 et
Viss(s)= Vi+1 - 2Vi + Vi-1
Ce qui nous permet de discrétiser la formule de Ei:
énergie au point Vi sous la forme:
Ei totale(Vi-1, Vi, Vi+1) = E int(Vi-1, Vi, Vi+1) + E
image(Vi) + E cont(Vi).
Et donc l'énergie totale du snake vaut:
E totale(Vi-1, Vi, Vi+1) = somme (Ei) = somme (Ei
int(Vi-1, Vi, Vi+1) + Ei image(Vi) +
Eicont(Vi))
(III.15)
III.2.2.1.2 Application pratique au cas du contour
actif : [02]
Appliquons cette méthode à notre Snake.
Nous partons d'un premier contour initialisé par l'utilisateur
lui-même. Nous allons le parcourir progressivement et en chaque point
éventuellement déplacer le point pour que sa nouvelle position
optimise l'énergie du Snake.
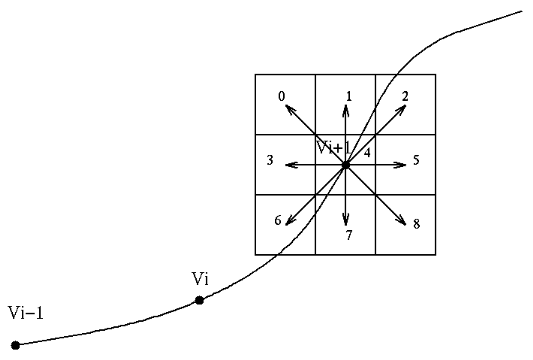
Chaque point a 9 déplacements possibles a chaque
étape comme le montre la figure suivante:
III.2.2.2 Les contours actifs
géométriques : ensemble de niveau ''Level
Set'' :
| 


