4- Effets des taux d'intérêt :
Adam Smith propose de réglementer les taux
d'intérêt afin d'éviter les comportements de prise de
risque immodérée des spéculateurs qui sont à
l'origine du risque de défaut auquel elles ne peuvent se
protéger, ni protéger la société .Il n'y a pas de
régulation de marché efficace mais une défaillance de ce
dernier. En quelque sorte, ce type de réglementation joue le rôle
de régulation prudentielle indirecte. En effet A. Smith montre que
l'existence d'un taux d'intérêt très élevé
(au-delà du taux normal du marché sur les meilleurs signatures)
sur les emprunts tend à augmenter la demande des emprunts trop
risqués (les «faiseurs de projets ») car ils peuvent seuls
envisager de payer les charges de remboursement (le rendement de leur projet
est élevé mais leur probabilité de remboursement est
faible)17au détriment de celle des « hommes prudents
» (effet d'antiselection). Ce sont justement ces mauvais emprunteurs qui,
notamment en émettant les « lettres de change circulantes »
indétectables par les banques, les
16 Shumpeter(1939), traduction original de«
the role of Money and Banking in the Process of Evolution »,chapitre 3,de
Bisiness Cycles : A Theorical Historical and Statical Analysis of the
Capitalist Proces,volume 1,1939 .
17 A.Smith (1776),p446
conduisent à la faillite et à la
destruction de capital. Le seul moyen de les empêcher est alors une
action indirecte de l'Etat qui fixe un plafond réglementaire au taux
d'intérêt : on limite ainsi l'afflux de ces « mauvais »
emprunteurs et évite l'éviction des bons. Même analyse
faite par J. Stiglizt en citant cette remarque de Smith. Le modèle de
Stiglizt-Weiss (1981) donne, en effet, des éclaircissements sur l'effet
de taux d'intérêt haut mais aussi d'un niveau bas des taux
d'intérêt (vor encadré).
Rationnement du crédit
|
J. Stiglitz et A. Weiss (1981) presentent un modele de
rationnement de credit dans lequel, parmi des emprunteurs identiques, certains
regoivent un prat et d'autres non. ~ We reserve the term credit rationing
for circumstances in which either (a) among loan applicants who appear to be
identical some receive a loan and others do not, and the rejected applicants
would not receive a loan even if they offered to pay a higher interest rate ;
or (b) there are identifiable groups of individuals in the population who, with
a given supply of credit, are unable to obtain loans at any interest rate, even
though with a larger supply of credit they would * J. Stiglitz et A. Weiss
(1981, p.394- 395).
Les emprunteurs potentiels qui ont ete rejetes ne
pourront pas emprunter, meme s'ils indiquent leur volonte de payer plus que les
taux d'interets du marche. Dans ce contexte, le taux d'interets qu'un individu
accepte de payer agit comme un moyen de discrimination car seules les
entreprises dont le projet est a haut risque accepteraient d'emprunter a de
telles conditions. Par consequent, l'accroissement du taux d'interet peut
accroitre le risque du portefeuille de prat de la banque en provoquant une
degradation de la qualite et donc de la rentabilite des actifs bancaires, dans
la mesure o:, elle se traduit par un accroissement de la proportion de mauvais
emprunteurs, ou si elle incite au developpement de projets plus risques (qui
ont d'ailleurs une probabilite de succes plus faible mais des rendements plus
eleves en cas de succes).
Ainsi, un taux d'interet unique ne peut equilibrer le
marche du credit. S'il est trop bas, la rentabilite des prets n'est pas
assuree, s'il est trop haut les projets les moins risques seront dissuades.
L'equilibre va se faire par les quantites. Les emprunteurs qui semblent les
plus risques sont rationnes. Dans ces circonstances, les restrictions de credit
prennent la forme d'une limitation du nombre de prets et non d'une limitation
de la taille de chaque prat ou d'une limitation par le taux d'interet paye en
faisant dependre celui-ci de l'amplitude du prat. L'appreciation realisee par
le banquier ne permettrait pas de s'approcher autant qu'il serait souhaitable
d'une tarification individuelle du risque de credit.
Il est donc interessant de noter ici que, lorsqu'il
n'est pas possible d'evaluer la probabilite de defaillance associee aux
demandes de credit des emprunteurs potentiels, la banque risque, en augmentant
ses taux, de selectionner les projets les plus risques (antiselection) ou bien
d'inciter les emprunteurs, après l'obtention de leur prêt, a
choisir des projets plus hasardeux pour accroitre leur gain en cas de reussite
(alea moral). La selection adverse temoigne par consequent de la difficulte
pour les investisseurs a discerner les meilleurs projets (M. Cherif,
1999).
3. STIGLITZ ET A. WEISS w Credit rationing in
markets with imperfect information * The American Economic Review, 1981,
vol. 71, n°3, pp. 93-410.
M. CHERIF w Asymétrie d'information et
financement des PME innovantes par le capital-risque * Revue d'Economie
Financiere, 1999, n°54, pp. 163-178.
|
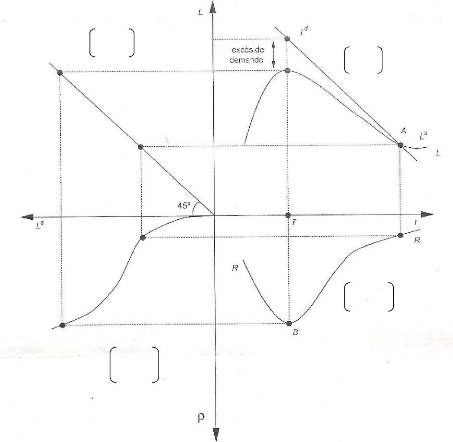
Graphique 3 : Le modèle de rationnement du
crédit de Stiglitz et Weiss (1981)

4
3
1
2
Hypothèses :
Considérons une économie composée
d'une banque et d'un groupe d'emprunteurs ayant chacun un seul projet sur une
période. Chaque projet requiert un montant fini de fonds L, que chaque
promoteur doit obtenir pour monter son projet. Chaque emprunteur doit en
garantie une valeur C, avec C < L.
On va aussi faire l'hypothèse que chaque projet
requière un financement avec une distribution de remboursement F qui
dépend de R et O.
R : est le rendement du projet.
O : est le risque du projet.
Alors F = F(R, O).
Modèle :
Les projets rapportent R s'ils sont fructueux ou 0
s'ils échouent. L'emprunteur ne peut en aucun cas influencer R. Une
valeur plus élevée de O est considérée comme
représentant d'une augmentation du risque du projet.
L'emprunteur reçoit le montant fixé de
prêt L au taux d'intérêt contractuel r et les défauts
sur les prêts si le rendement du projet R plus (+) la valeur de la
garantie C sont insuffisants pour rembourser le projet.
La banque reçoit soit le montant contractuel total
(1+r)L soit le maximum possible R+C. Le rendement de la banque est donné
par le minimum de ces 2 valeurs :
Min{R+C, (1+r)L} ;
Comme le projet rapporte un rendement nul s'il
échoue, le rende ment de l'emprunteur est donné par :
Max{R - (1+r)L, -C} ;
Stiglitz et Weiss montrent que pour un taux
d'intérêt donné, il existe une valeur critique de O
notée õ telle qu'un agent empruntera pour investir si O >
õ. C'est-à-dire que le taux d'intérêt sert
d'instrument de sélection.
Le cadran (1) du graphique présente la demande
de prêt Ld et l'offre de fonds prêtable Ls.
La fonction de demande de prêt Ld est
représentée de façon standard comme une fonction
décroissante du taux d'intérêt r. Au contraire l'offre de
fonds Ls est considérée positivement liée au taux
d'intérêt jusqu'à un niveau ?, au-delà de ? l'offre
de fonds est une fonction décroissante du taux d'intérêt.
Les augmentations du taux d'intérêt au delà du taux
d'intérêt optimal de la banque entraine deux types de faits : un
effet de sélection adverse qui se traduit par une augmentation de la
valeur seuil õ et qui provient du fait qu'en augmentant le degré
de risque du groupe des candidats, les emprunteurs à faible risque se
retirent du marché. Deuxièmement, un effet d'aléa moral
qui apparait car d'autres emprunteurs sont appelés à choisir des
projets pour lesquels la probabilité d'échec est
élevée car en retour les projets plus risqués sont
associés à des rendements espérés plus
élevés. Des augmentations du taux d'intérêt
entrainent des effets de
sélection adverse et d'alea moral qui en
réduisant le taux de rendement attendu de la banque induisent des
montants de croissance faibles de crédits faits aux emprunteurs. Par
conséquent, la relation entre l'offre des fonds prêtables et le
taux d'intérêt contractuels devient négative et la valeur
de Ls décroit à droite de ?. La courbe de fonds prêtable
à une forme concave. Le taux de rendement espéré de la
banque noté ñ est le produit du taux d'intérêt
contractuel et de la probabilité de remboursement. En raison des effets
de sélection adverse et d'alea moral associé à
l'augmentation de r, la probabilité de remboursement baisse plus que
l'augmentation du taux d'intérêt au-delà du niveau seuil du
taux d'intérêt ?. Ainsi, la relation entre le taux de rendement
ñ et le taux d'intérêt r est donc non monotone comme
l'illustre la courbe RR du cadran (2). Un taux de rendement attendu plus
élevé augmente l'incitation à prêter ; il y a donc
une relation positive entre ñ et l'offre de prêt Ls
comme indiqué au cadran (3).
En fin le cadran (4) représente une ligne à
45o correspondant au montant des prêts
d'équilibre.
La valeur du taux d'intérêt contractuel
d'équilibre qui assure l'égalité entre l'offre et le
demande prêtable est obtenue au point A du cadran (1). Cependant,
l'équilibre de rationnement du crédit caractérisée
par un excès de demande est ?*. A ce taux d'intérêt, le
rendement ñ attendu de la banque est à son niveau maximum. Pour
la banque, le taux d'intérêt d'équilibre r* n'est pas
optimal car c'est à ? que le rendement est maximum (mais à ? il y
a rationnement).
L'hypothèse de rationnement du crédit de
Stiglitz et Weiss semble utile pour comprendre dans certains pays en
développement, notamment ceux des pays africains, le crédit est
sévèrement rationné avec des taux débiteurs des
banques insensibles à l'excès de demande de
crédit.
Le modèle de Stiglitz et Weiss permet aussi de
comprendre pourquoi dans nos pays, les banques commerciales détiennent
des réserves excédentaires de liquidité.
Dans un environnement dans lequel la probabilité
de défaut sur les engagements de prêts est élevée,
les réserves excédentaires tendent également à
être élevées.
| 


