La théorie de la gravité quantique de Bohm dans l'approximation linéaire du champ

Conclusion Générale

En définitive, dans ce mémoire, il était question de présenter la théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ, tout en la comparant à l'actuelle théorie classique de la gravitation. Cette comparaison a été faite en faisant l'approximation newtonienne de chacune de ces théories, et en les appliquant chacune au cas de la solution SSS. Pour conforter la théorie de BOHM, la solution SSS a été utilisée pour décrire le phénomène de la déviation de la lumière (auquel nous avons ajouté les applications du mirage gravitationnel et du décalage spectral des fréquences ceci en fonction de la solution SSS). On a vu que des observations concrètes pouvaient être possibles, ce qui est un succès de la théorie de BOHM. Compte tenu de tout ceci, nous pensons que cette théorie devrait être prise au sérieux en tant qu'approche de la gravité quantique au même titre que les autres [1, 4]. Toutefois, avant d'acquérir le statut de véritable théorie de gravitation quantique, certains points encore obscurs devront être résolus. Nous pensons qu'il faille davantage la formaliser, l'étendre aux termes non linéaires du champ. Nous devront alors l'utiliser pour avoir une véritable explication des phénomènes gravitationnels et de l'Univers dans son ensemble (comme toute bonne théorie de la gravitation quantique, c'est à ce titre que les autres approches prétendent). La théorie de la gravitation quantique de BOHM en unifiant les quatre (04) interactions fondamentales réalise ainsi le rêve des théoriciens de la physique comme Albert EINSTEIN (théorie unitaire déterministe) tout en constituant un vaste champ fertile de la recherche fondamentale qu'il faut explorer par des expériences concrètes et surtout par celle de la pensée.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Annexe des équations I- Chapitre 1

1. Obtention de l'équation (I.12)

(I.12)

2. Obtention de l'équation (I.23)

or

Donc on aura :

(I.23)

3. Obtention de l'équation (I.33)

? ? ?

R ? exp i at

?

e ? ?2 2 ? ? VR e

R

?

ih

t

i ? e

1

?

²
1

e

aS i ? ² i S i S ?

?

? ? R e

( )

?

? ?

m
h

? 2

R ? V e i ? ?

? ? ?

R S 2m 2m h

? ? ? ?? ? ?

i ? ? ? ? ? ? ? ?

?

On effectue touts les simplifications possibles, notamment on simplifie par

? ?

e i R

? e ² R e ? ? ? ?

?

? ? ? ? R S e ? VR e i

? ? ? ? ?

R S e dans les deux

? ?? ?? ? ? ? 2

membres de cette relation on obtient :

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

m

S

m ]

S

;

? ?Ras m2

m

? S ? hi2 ? VR S

Rm(

R m

m m

Si on divise cette dernière relation par R on obtient :

Regroupons à gauche les termes imaginaires et à droite les autres :

Pour que cette dernière relation soit solvable, il faut que ses deux membres soient identiquement nulles :

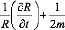
Multiplions la première équation de ce système par 2R :

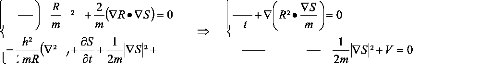
aS 2

m

SV =o L ? ? ? ?

S V ? t m

at

2

(I.33)

S

+ ? ? ?

RV

S S ?

P:

S

R

t

4. Obtention de l'équation (I.36)

· m or v d e f (t) ?	dt ? ? ? m	m V		+

?² ?

^m V(v")+VV v ? ? ?

V Q or 0

?

dt 2

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

On donc :

(I.34)

II- Chapitre 2

?

1. Obtention de l'équation (II.5)

La densité du Hami ltoni en en fonction de celle du Lagrangien : ? ?

or d'après (II.3),

[

O fivaR.Ogv = 2 _fiv^iiv tell_A.

1 [ u
· # v 00

P tel

(II.5)

12. Obtention de l'équation (II.8)

? ? ? ^?

d'après (II.5)

De (II.6) on a:

?

V ?	? 8 8 1 3 ?? 1 ?

L'équation s'écrit alors :

(II.8)

3. Obtention de l'équation (II.10)

3 dans l'approximation linéaire du champ

x ' ' ? ? ? ?

? ??

? ? x ' '

? ? x '

? ?

S S

? 1' = ¹ f d³ xv o_' ,,(xi)v e^v'(x^{i 2}

4. Obtention de l'équation (II.13) On sait d'après (II.4)

<=> Thy

(II.13)

5. Obtention de l'équation (II.14)

Or

S

? 0

? a

at ? ?

? ?

x ??

? ??

De même ?

		pression=d (cx nditioi de jauge)		? ? ?
1
? 60 ? ?			V

6

? ?

f ^d3x ' [0 i ' iv ' .^j cr]

2 _iew p J P ₍50Pv

d Dansle premier membre on fait : 6Q

³

? ? ?? ?

On doit faire

, est symétrique de signature

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

? q

si l' ?

? ' d³ x'V''² O_{p 2} ? + 0

(II.14)

6. Obtention de l'équation (I1.18)

(II.18)

7. Obtention de l'équation (II.19)

Rx 6 ? ? ax S ? ? ? ? +4 8 [R2 8 S .1cPx' at 80(xx 80(.0 ? x = 0 ? 8. Obtention de l'équation II.21

(II.19)

qti srira

e Bx H M (11' 13) s'écrit. Op. _ d 31 äö x' 2 ?

²:

? 4 ? d x ?

RCe qui conduit à

?ä '

? ?

?

(II.21)

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

9. Obtention de l'équation (II.23)

(II.23)

10. Obtention de l'équation (II.28)

^R 80(x)2 2 ?R ^?801⁸0 ?

2

? ?

Q'= R - 1 80 d³x x a Q 0c )R}en R fér³tint pa( ?

) R

? 1

?

? Q= 2ah²[1- 04 ?

(II.28)

?cY

11. Obtention de l'équation (II.29)

-a

2

V²0= -4A^-G + a^{2 2 8}(0^-0

? 2 80 ?

?

(II.29)

(II.32)

(II.34)

aB (sin Y +

Théorie de la gravité quantique de BOHM Par MANDENG .M. Lucien (E.N.S 06 #177;07)

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

12. Obtention de l'équation (II.31)

14. Obtention de l'équation (II.32)

1 [0c 2 0,₇q = ^--4A^-1 Ma( X) ^--ia^{2 2} (q ^--0^c ) V²0^c #177; V²q,₇ ? ? ? ? ? ?

^{2 2}

? d " ?II r ₃₁ sin V2 ? -- ^?2 2 r ² ? ?V2 2 ?

16. Obtention de l'équation (II.33)

d 1 U ? ?

r 2 1^,.2 sinr

ao

1+ ^{s a 1.2sin° a°}aO q)#177; 1 a rUsY ?

r2 sin O ar arsin

(II.33)

15. Obtention du système (II.34)

? ? 0 0

? ? ? ?U(r)Y(9 ) ( ^{d (}r²ⁿ Uj+ U a i_sine²sin + U n ay) r r2sint9 ?

at9L ? ¹ ? ?

e ) r sin B app app

16. Obtention de l'équation (II.43) ? ? ? ? ?

(II.31)

57

dans l'approximation linéaire du champ

(II.43)

17. Obtention de l'équation (II.46)

? ?v ( ) v

(oF - 8 " )

(II.46)

18. Obtention de l'équation (II.47)

a r 2a a 2 2

?

1¹ a

?

R

8 80

			(II.47)
	V

?

? ? ?

? ? ? ?

( _q

1 ?

4 19. Obtention de l'équation (II.48)

? ? ?

? ?? ?

??

? ² ?

or donc

	(II.48)