Inventaire et hiérarchisation de paramétres structuraux et ultrastructuraux de la variabilité intra spécifique de certaines propriétés mécano physiques des tissus ligneux

3.4.3 Influence du module élastique de la matrice

Divers auteurs (Salmèn et al, 1985, Bergander, 2001), ont montré que les propriétés

mécaniques des hémicelluloses et lignines, influencent, de manière significative, les modules transverses de double paroi fournis par des modélisations multicouches à fibres parallèles anisotropes et très peu le module bipariétal longitudinal.

Pour hiérarchiser les paramètres ultrastructuraux responsables à priori de l'anisotropie des deux doubles cloisons envisagées (M2 et M3), une comparaison de l'influence du module d'élasticité de la matrice sur les modules de double cloison est menée. Ces deux modélisations font toutes les deux appel à la valeur optimisée du module de microfibrille (62

GPa, présentée au chapitre 2) et attribuent un comportement isotrope aux fibres.

L'étude est menée à partir d'un composite stratifié à 9 couches dont les caractéristiques micromécaniques ultrastructurales sont rappelées au Tableau 3.9.

86

Hiérarchisation des paramètres descriptifs de l'anisotropie élastique du bois normal

Pour chaque modèle (M2 et M3), et pour différents modules de matrice, les variations des

modules élastiques homogénéisés ELp et ETp avec l'AMF (ö) sont traduites dans le Tableau

3.10 et sur les Figures 3.17 et 3.18.

Sous couche	S1	S2	S3	LM
E^m(GPa)	variable	variable	variable	variable
E^f	62	62	62	62
V	0,3	0,5	0,5	0,1
í^m	0,3	0,3	0,3	0,3
í^f	0,1	0,1	0,1	0,1
AMF ö (en °)	+/- 60°	variable	60	90

Tableau 3-9 Paramètres ultrastructuraux du modèle multicouche M2

	E^m= 1GPa				E^m= 2GPa				E^m= 3GPa
AMF (ö) dans ^S2 ^(en °)	Multicouche M2		Squelette M3		Multicouche M2		Squelette M3		Multicouche M2		Squelette M3
	^ELp	^ETp	^ELp	^ETp	^ELp	^ETp	^ELp	^ETp	^ELp	^ETp	^ELp	^ETp
5	22,56	5,11	31,67	1,14	24,32	8,39	32,34	1,82	24,32	8,39	33,02	2,49
10	21,65	5,12	31,64	2,51	23,49	8,41	32,32	3,19	23,49	8,41	32,99	3,86
15	20,19	5,20	31,53	4,69	22,17	8,49	32,21	5,36	22,17	8,49	32,88	6,03
20	18,31	5,39	31,25	7,50	20,45	8,67	31,92	8,17	20,45	8,67	32,60	8,85
25	16,13	5,77	30,68	10,76	18,47	9,02	31,36	11,43	18,47	9,02	32,03	12,10
30	13,81	6,41	29,74	14,24	16,35	9,61	30,41	14,91	16,35	9,61	31,08	15,58
35	11,48	7,36	28,32	17,72	14,22	10,48	28,99	18,39	14,22	10,48	29,66	19,06
40	9,28	8,66	26,38	21,00	12,22	11,67	27,05	21,67	12,22	11,67	27,73	22,34
45	7,33	10,31	23,92	23,92	10,43	13,17	24,60	24,60	10,43	13,17	25,27	25,27
50	5,68	12,26	21,00	26,38	8,93	14,96	21,67	27,05	8,93	14,96	22,34	27,73

Tableau 3-10 : Comparaisons des variations des modules élastiques du multicouche M2 avec l'AMF(ö)

87

Hiérarchisation des paramètres descriptifs de l'anisotropie élastique du bois normal

Figure 3.17 Evolutions des modules élastiques de double paroi prévus par le modèle M2 avec l'angle des

microfibrilles (ö) et influence du module de la matrice ligno cellulosique

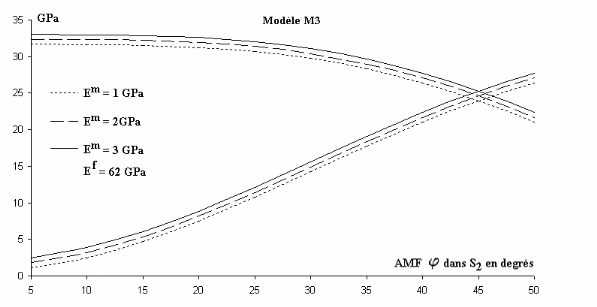
Figure 3.18 Evolutions des modules élastiques prédits par le modèle M3 avec l'angle des microfibrilles (ö).

Influence du module élastique de la matrice ligno cellulosique.

L'examen du Tableau 3.10 et de la Figure 3.17 permet de noter l'importante sensibilité des

^ELp ^{et E}Tp ^{du modèle M2 au module élastique Em de la matrice. Cette tendance est}

particulièrement marquée sur le module transverse ETp. Elle s'explique essentiellement par l'association en série de la matrice et des microfibrilles dans les directions transverses des différentes plaques composites (relation 2.3 du chapitre 2). L'association en parallèle des mêmes éléments conduit à une moindre sensibilité du module longitudinal ELp du modèle M2.

Le paramètre E^m est donc un paramètre sensible pour une modélisation multicouche de la double paroi.

Les modules homogénéisés ELp et ETp du Squelette M3 sont quant à eux, bien moins dépendants des valeurs de E^m employées (Tableau 3.9 et Figure 3.18). L'expression des ELp

et ETp (fonction affine de E^m, à (ö) fixé, relations 2.27 et 2.28 du chapitre 2) constitue

88

Hiérarchisation des paramètres descriptifs de l'anisotropie élastique du bois normal

l'explication de cette quasi insensibilité. Le modèle M3 accorde en effet un rôle majeur au

renfort filamentaire et donc à un de ses paramètres descriptifs essentiel l'angle des microfibrilles dans S2 (ö). Puisque les transferts d'efforts ne sont pris en charge, dans M3, que par le squelette de fibres cellulosique, il n'apparaît pas nécessaire de faire appel à un paramètre descriptif de l'état mécanique de la matrice.