3.3 Rôle des rayons ligneux dans l'anisotropie
élastique du cerne
L'association bois « infi » et rayons ligneux
du chapitre 2 a notamment été établie en se basant
sur l'hypothèse selon laquelle une fraction volumique en rayons ligneux
(n) importante induit un renfort radial au détriment de la
rigidité longitudinale (Barkas, 1941).
On notera que la qualité des régressions
linéaires entre les modules d'Young macroscopiques
EL et ER de plusieurs essences et leurs masses volumiques
(ñ) a été améliorée (Guitard et
al,
1987) par la prise en compte du paramètre (n).
Comme le montrent la Figure 3.14 et le Tableau 3.7, le
paramètre (n) est donc un facteur qui intervient essentiellement sur
l'anisotropie L/R (facteur aLR) et L/T (aLT). Une valeur
élevée
de (n) conduit à une réduction de
l'anisotropie L/R (par une augmentation de ER et une diminution de
EL) et à une augmentation de l'anisotropie L/T (diminution de
ET plus
« rapide » que celle de EL).
|
n (%)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EL
(GPa)
|
13,30
|
13,18
|
13,10
|
12,92
|
12,80
|
12,67
|
12,55
|
12,42
|
12,30
|
12,17
|
12,04
|
|
ER
(GPa)
|
0,88
|
0,95
|
1,00
|
1,08
|
1,15
|
1,22
|
1,29
|
1,35
|
1,42
|
1,49
|
1,56
|
|
ET(GPa)
|
0,73
|
0,68
|
0,64
|
0,60
|
0,56
|
0,53
|
0,51
|
0,48
|
0,46
|
0,44
|
0,42
|
|
aLR
|
15,12
|
13,91
|
13,10
|
11,94
|
11,13
|
10,41
|
9,76
|
9,18
|
8,66
|
8,18
|
7,74
|
|
aLT
|
18,34
|
19,46
|
20,60
|
21,63
|
22,67
|
23,70
|
24,70
|
25,67
|
26,62
|
27,54
|
28,44
|
|
aRT
|
1,21
|
1,40
|
1,57
|
1,81
|
2,04
|
2,28
|
2,53
|
2,80
|
3,07
|
3,37
|
3,67
|
Tableau 3-7 Variations des coefficients d'anisotropie
avec le paramètre (n). Le bois étudié est le
RSV.
82
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.14 : Evolutions avec la fraction volumique en
rayons ligneux des différents facteurs d'anisotropie
3.4 Influence des paramètres ultrastructuraux
sur l'anisotropie élastique tissulaire
Les paragraphes précédents ont montré
que des coefficients d'anisotropie tissulaire L/T classiquement
rencontrés dans le bois normal, ne peuvent être expliqués
que partiellement par l'influence de la géométrie cellulaire et
de ses modifications (évolutions du rapport e/D via des variations de
porosité ou par une ovalisation radiale).
La masse volumique contribue à une rigidification
du matériau par effet « quantité de matière
». L'hétérogénéité tissulaire
densitométrique du cerne est un paramètre de second ordre
qui joue un rôle contradictoire à l'anisotropie élastique
R/T observée sur les résineux.
La fraction volumique en rayons ligneux est un paramètre
sensible tel qu'à une valeur élevée
de ce paramètre correspond une réduction du rapport
d'anisotropie L/R
L'objet de ce paragraphe est donc d'une part, de
préciser, numériquement, l'influence de quelques
caractéristiques ultrastructurales de la matière ligneuse
(module d'élasticité de la matrice, des fibres, inclinaison
(ö) des microfibrilles dans la sous couche S2) sur
l'anisotropie
élastique bipariétale (modélisation
de type Squelette) et d'autre part, de déterminer leur
influence directe sur les caractéristiques
élastiques tissulaires mésoscopiques.
3.4.1 Sensibilité de l'anisotropie tissulaire L/T
à l'angle des microfibrilles
Afin d'évaluer le rôle de l'inclinaison
des microfibrille (ö) sur l'anisotropie des
caractéristiques élastiques tissulaires, une
estimation de l'influence d'un accroissement autour
de valeurs particulières d'AMF (ö0) sur les
modules élastiques mésoscopiques de tissus est menée.
L'influence de l'ovalisation ayant déjà été
montrée (par l'intermédiaire du facteur aLT
lui-même dépendant du paramètre
d'ovalisation ë), il convient de rechercher les facteurs
complémentaires de variabilité de l'anisotropie élastique
du tissu à une échelle d'observation inférieure.
Posant c = cos (ö), s = sin (ö) et E
= VEf, le rapport d'anisotropie bipariétale L/T,
défini à partir des relations (2.27) et (2.28)
présentées au chapitre 2, s'écrit (3.17)
83
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
(3.17)
E Lp
=
E Tp
D Es 4
= F (ö)
D Ec 4
En ayant posé, pour alléger l'écriture ;
D = (1 V) (1 ) E m
(1 + )(1 2 )
+ VE f
|
Variation relative de l'anisotropie tissulaire L/T, pour des
variations d'angle (ö) exprimées en °
|
|
(ö0)
exprimé en°
|
Coefficient
S (ö0)
|
Valeurs de
F (ö0)
|
[+1]LT
|
[+2 ]LT
|
[1]LT
|
[2 ]
LT
|
|
5
|
-104,912
|
17,817
|
-0,115
|
-0,259
|
0,093
|
0,170
|
|
10
|
-65,618
|
10,139
|
-0,127
|
-0,292
|
0,101
|
0,184
|
|
15
|
-32,809
|
6,008
|
-0,105
|
-0,235
|
0,087
|
0,160
|
|
20
|
-17,381
|
3,905
|
-0,084
|
-0,184
|
0,072
|
0,134
|
|
25
|
-10,104
|
2,743
|
-0,069
|
-0,148
|
0,060
|
0,114
|
|
30
|
-6,410
|
2,040
|
-0,058
|
-0,123
|
0,052
|
0,099
|
|
35
|
-4,394
|
1,577
|
-0,051
|
-0,108
|
0,046
|
0,089
|
|
40
|
-3,228
|
1,248
|
-0,047
|
-0,099
|
0,043
|
0,083
|
|
45
|
-2,521
|
1,000
|
-0,046
|
-0,096
|
0,042
|
0,081
|
Tableau 3-8 : Variations relatives de l'anisotropie
tissulaire L/T autour de quelques valeurs d'AMF
ö0
choisies

Figure 3.15 Incidence sur l'anisotropie tissulaire L/T
d'un ajout de 1° et 2° autour de quelques valeurs d'AMF
ö0 choisies
84
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
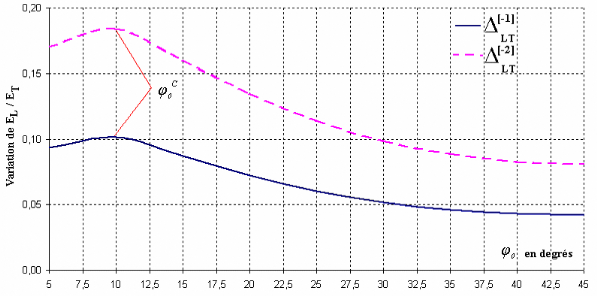
Figure 3.16 Incidence sur l'anisotropie tissulaire L/T
d'une soustraction de 1° et 2° autour de quelques
valeurs d'AMF ö0
Au voisinage d'un angle (ö0), le rapport
d'anisotropie L/T de la double paroi s'écrit
(développement limité de Taylor au premier ordre)
:
(3.18)
E Lp
D E s 4 ( )
4 E c (
) s (
) [(Ec 4 (
)s 2 (
) + Ec 2 (
)s 4 (
) - D)]
= 0
+ (
0 ) 0 0 0 0 0 0
E Tp
+ è ( 2 )
D E c 4 ( 0 )
(D Ec 4 ( 0
)) 2
La sensibilité de ce rapport à l'angle des
microfibrilles (ö) dans S2, autour d'un angle
(ö0) est
donc exprimée (3.19) par le second terme du
deuxième membre de l'équation (3.18), noté
S(ö0)
4Ec (
)s (
) [(Ec 4 (
)s 2 (
) + Ec 2 (
)s 4 (
) - D) ]
(3.19)
S(
) = 0 0 0 0 0 0
0 (D Ec 4 (
0
)) 2
Le rapport d'anisotropie tissulaire mésoscopique L/T peut
donc s'écrire sous la forme (3.20)
0
E L
D E s 4 ( )
(3.20)
= a LT
E T D E c 4
( 0 )
+ (
0 ) S( 0 )
Il est alors possible de définir la variation relative,
LT
[ ]
0
du même rapport d'anisotropie
0
tissulaire L/T pour des variations positives ou
négatives [ ]
autour de chaque valeur
d'angle (ö0) (Tableau 3. 7, ou les divers angles
sont exprimées en degrés)
85
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
(
).S( )
(3.21)
? LT[ 0 ] = 0 0
( 0 ).S( 0 ) + F(
0 )
Les valeurs numériques attribuées aux
« coefficients de sensibilité »
S(ö0) permettent de
montrer (Tableau 3.8) l'existence d'une zone de
sensibilité maximale de l'anisotropie L/T du
tissu, située aux alentours de 10 degrés (angle
correspondant à un bois final).
0
L'examen du Tableau 3.8 et des Figures 3.15 et 3.16,
définit comme valeur critique ( ö c
)du
paramètre (ö), la valeur de 10
degrés, autour de laquelle les variations de l'anisotropie L/T sont les
plus importantes. Ainsi une augmentation de 1 degré autour de 10
degrés conduit à une diminution de plus de 12% de l'anisotropie
L/T, une augmentation de 2 degrés conduit à une chute de plus de
29% du rapport L/T.
On remarque également (Figures 3.15 et 3.16) que plus
l'angle des microfibrilles dans S2 (ö)
est élevé, moins l'anisotropie tissulaire
mésoscopique L/T en est dépendante. Dans notre
modélisation, un bois caractérisé par une
valeur élevée d'angle des microfibrilles (ö) dans
S2
(bois initial, bois juvénile, éventuellement
bois de compression) verra donc son rapport
d'anisotropie tissulaire L/T moins sensible à ce
même paramètre qu'un bois possédant une plus faible
inclinaison microfibrillaire (bois final) dans la même sous couche.
L'angle (ö) des microfibrilles dans la sous couche S2
constitue cependant une composante essentielle de
l'anisotropie élastique tissulaire.
3.4.2 Incidence du module d'élasticité des
microfibrilles
A l'échelle de la sous couche
élémentaire, les différentes modélisations du
comportement
élastique bipariétal (Multicouches ou
Squelette) considèrent, une association en série
« matrice - fibres » dans la direction
longitudinale de la cellule et une association parallèle dans
les directions transverses. Compte tenu de la relation d'ordre entre
les modules longitudinaux de microfibrille employés (supérieurs
à la centaine de GPa) et les modules de matrice
généralement admis (de l'ordre de 2 GPa), le module
d'élasticité longitudinal des microfibrilles constitue, quelque
soit la modélisation, un paramètre déterminant de
l'élasticité
(longitudinale ou transverse) de la double paroi.
Une étude de l'influence du module
d'élasticité des microfibrilles sur les
caractéristiques élastiques de la double paroi sera menée
plus loin.
|
|



