3.2.2 Distinction densitométrique entre le bois
initial et le bois final
Les profils de densité intra cerne ne laissent
généralement pas apparaître de transition abrupte
lors du passage bois initial bois final (Holmberg
et al, 1999, Leban, 1999a, 1999b). La pertinence d'une
démarche de discrétisation du cerne (bois initial/bois
final) en terme de densité demande donc à être
évaluée en regard de quelques résultats
proposés dans la littérature.
Des modélisations prédictives des variations
intra cerne de la masse volumique du bois ont été
présentées pour différentes espèces de
gymnospermes (Leban, 1999a, 1999b). Si ces descriptions analytiques
sont belles et bien spécifiques à chaque genre de
résineux, elles présentent néanmoins l'avantage
d'être assez proches les unes des autres au niveau de leur
formulation.
Ces modèles segmentés, considèrent ainsi que
l'évolution de la densité dans le cerne, peut être traduite
par un raccordement de 3 fonctions affines « densité,
position dans le cerne »
(correspondant aux zones dites de bois initial, zone de
transition, bois final).
72
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Les meilleures estimations (corrélations statistiques) de
l'évolution de la densité intra cerne
sont obtenues (Leban 1999a, 1999b) en associant des
paramètres caractéristiques de chacune des zones
précédentes à l'âge et à la largeur de cerne,
comparativement à celles associant une variation de masse volumique
moyenne à la largeur des cernes et à leur âge. La
discrétisation
du cerne, en terme de densité (bois initial, final, zone
de transition) est donc envisageable.
Pour établir « numériquement » une
limite entre le bois initial et final, la méthode la plus
couramment utilisée, et employée dans la suite de
ce chapitre (utilisation de profils microdensitométriques),
consiste à définir la frontière entre les deux
types de bois, par la moitié de la différence entre le
maximum et le minimum de densité de chaque cerne, ce qui permet
alors, de s'affranchir des variations de densité inter cerne
(Mäkinen et al, 2002, Leban,
1999b).
En conclusion, s'il apparaît difficile d'établir un
critère géométrique reproductible permettant
de distinguer, pour toutes les essences résineuses, les
deux types de cellules dites initiales et finales, la discrétisation
possible du cerne d'accroissement en terme de densité ainsi que
l'examen microphotographique confirment l'existence d'une réelle
hétérogénéité tissulaire. Les paragraphes
précédents ayant montré l'importance de la
porosité et de la morphologie cellulaire respectivement sur les
rapports d'anisotropie élastique à l'échelle du
cerne et à l'échelle tissulaire, il apparaît
nécessaire d'évaluer l'influence, sur ces mêmes rapports,
de la présence des deux catégories de cellules (bois
initial et final) et de caractériser
« mécaniquement » la transition de l'une
à l'autre.
3.2.3 La texture, facteur d'anisotropie élastique dans
le plan transverse
Comme cela a été indiqué
précédemment (chapitre 1), le bois présente une
hétérogénéité
selon la direction radiale à l'intérieur d'un
même cerne de croissance ; ceci s'explique par le passage progressif d'un
tissu ligneux, de porosité élevée, adapté à
la conduction de la sève, vers un tissu plus dense à parois
cellulaires plus épaisses, mieux adapté à la
fonction mécanique de support.
Les modèles mécaniques tissulaires
présentés dans le deuxième chapitre (Passage
3) permettent de préciser les effets de l'ovalisation des
cellules et de la modification de l'épaisseur de paroi, sur
l'anisotropie élastique transverse. L'ovalisation des cellules est
schématisée sur la Figure 3.5a, par la diminution du
diamètre radial DR par rapport au diamètre tangentiel DT,
lorsque l'on progresse vers le bois final. Ceci correspond assez bien,
d'après la bibliographie présentée au paragraphe
précédent, à ce qui est observable, en
première approximation, sur la majorité des plans ligneux de
résineux (la Figure 3.5 b en est
un exemple sur Picea abies).
Pour apprécier l'influence de l'ovalisation cellulaire,
l'analyse est menée en premier lieu en se plaçant dans les
conditions particulières suivantes.
3.2.3.1 Ovalisation radiale
La cellule de départ est choisie carrée et
représentative (via la masse volumique fixée à
0,35g/cm3 d'un tissu de bois initial. Le passage du
bois initial au bois final, est alors, à cette étape de la
discussion, simulé par une unique variation continue du
diamètre radial. Cette transition aboutit donc à une
morphologie cellulaire rectangulaire dont les caractéristiques sont
précisées par la relation 3.11
73
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
(3.11) ETp= ERp , eT =
eR= e
DT = D DR= ë D avec ë = 1
Les paramètres géométriques épaisseur
de paroi et diamètre tangentiel sont fixés, d'une part, avec le
soucis d'être réalistes en regard de la bibliographie (Tableaux
2.3 et 2.6 du chapitre 2)
et d'autre part de manière à obtenir une
masse volumique cohérente en regard de divers profils
microdensitométriques.


R
T
Figure 3.5 (a) Ovalisation selon la direction
radiale, (b) coupe transversale de P. abies colorée à
la
safranine et au bleu alcyan, Ruelle (2003),
montrant un quasi alignement des parois radiales
(grossissement x 500, barre d'échelle 25
um)
Sous ces restrictions, les relations (2.15 du
chapitre 2), (3.1) et (3.2) deviennent respectivement (3.12), (3.13)
et (3.14):
e 1
e
(3.12) = m (1-Po) = 2 m D + 1 - 2 D
E 2e
1 E E
(3.13)
L =
1
+ Lp
= a LR Lp
ER
ëD ë ETp
ERp
E 1
e ëD
3
e E E
(3.14)
L
= 1 +
2
1 2
+ ë
Lp
Lp
a LT
E T
64 D e
D E Tp
E Tp
Le rapport d'anisotropie transverse tissulaire
(mésoscopique) s'écrit enfin (3.15)
E 1
e ëD
3 E
(3.15)
R
= 1 +
2 Rp
E T
64 D e
E Tp
=
74
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Les trois coefficients aLR, aLT
et aRT ainsi définis, caractérisent
l'influence de l'ovalisation
des cellules sur l'anisotropie élastique du tissu
ligneux.
Les Figures 3.6 et 3.7 illustrent les modifications des
coefficients géométriques d'anisotropie associées à
une diminution du diamètre radial DR par rapport au diamètre
tangentiel DT. Les applications numériques sont conduites à
partir d'un facteur de forme e/D= 0,06, qui correspond pour des cellules
carrées à une masse volumique de 0,35 g/cm3 (bois
initial).
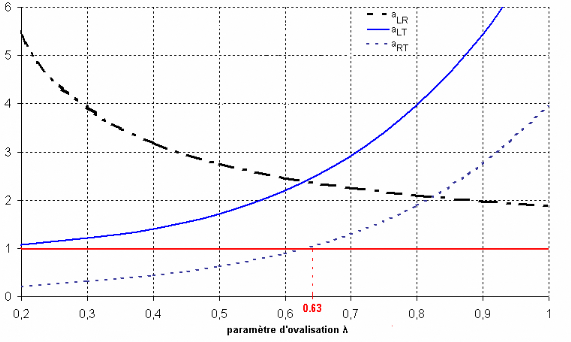
Figure 3.6 : Variations des coefficients d'anisotropie
tissulaires en fonction du paramètre d'ovalisation ë

Figure 3.7 : Evolution du paramètre d'ovalisation
ë en fonction de la densité
Dans ces conditions, on constate que, pour des valeurs
de DR décroissantes, la masse volumique augmente, d'où une
diminution de la porosité et d'autre part, que les facteurs aLT et aLR
évoluent en sens opposés. Ceci se traduit (Figure 3.6)
par un coefficient géométrique
75
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
d'anisotropie dans le plan transverse aRT qui
devient inférieur à 1, pour ë = 0,63, c'est à
dire
une masse volumique de 0,43 g/cm3 (Figure
3.7), avec pour conséquence directe une inversion de l'anisotropie
dans le plan transverse.
Sous l'effet de ce seul paramètre
géométrique ë (on rappelle ici l'absence des rayons ligneux,
éléments essentiels de renfort radial), le module
d'élasticité tangentiel ET d'un tissu, assimilable par
la forme de ses cellules à un tissu de bois final,
deviendrait supérieur au module ER, contrairement à des
propositions bibliographiques statistiques (modèles
prévisionnels l'anisotropie élastique, Guitard, 1987).
En outre, des rapports d'anisotropie élastique L/T
(facteur aLT) de l'ordre de 20 ne peuvent être obtenus par seul effet
de l'ovalisation résultant d'une transition d'une cellule de
bois initial vers une cellule de bois final.
3.2.3.2 Etablissement d'un lien entre variations
d'épaisseurs pariétales et diamètre radial
Associant microphotographies et études
microdensitométriques sur Picea abies, Holmberg et
al (1999), suggèrent une croissance lente
de la densité dans le bois initial liée à une
augmentation modérée de l'épaisseur, à
diamètre radial constant. Pour ces derniers auteurs, dans la zone de
transition, l'épaisseur pariétale augmente rapidement (avec pour
conséquence directe une croissance rapide de la densité), tandis
que le diamètre radial décroît. Dans le bois final, si la
densité croit lentement, le diamètre radial demeure constant
alors que l'épaisseur de paroi augmente.
Pour compléter l'étude précédente, en
tenant compte des liens probables (non explicités dans
la littérature) entre les variations
d'épaisseurs pariétale et celles du diamètre radial,
une simulation analytique des modifications des rapports d'anisotropie
tissulaire est réalisée à partir de profils
microdensitométriques sur du bois adulte de Picea abies fournis
par P. Rozenberg (INRA Orléans, Unité d'Amélioration,
Génétique et Physiologie Forestière).
Le choix de l'accroissement annuel utilisé (zone B) s'est
fait :
d'une part avec la volonté de ne pas avoir un profil de
densité trop irrégulier (reprise
de croissance, zone A sur la Figure 3.8)
afin de disposer de la plus large gamme de
relevés densitométrique (la zone B est
préférée à la zone C).
76
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
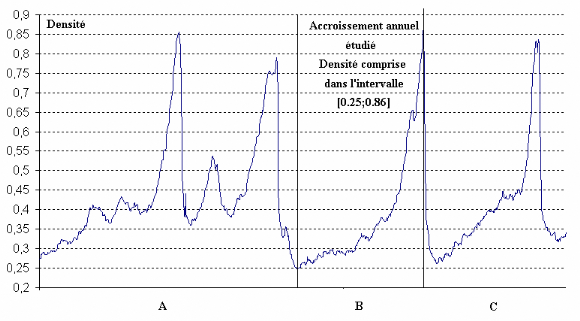
Figure 3.8 Exemple de profil microdensitométrique
d'étude sur P.abies (données numériques fournies
par
Rozenberg). Densité mesurée par absorption
d'un rayonnement X
3.2.3.2.1 Lien entre l'épaisseur et le diamètre
radial via la masse volumique
La morphologie de la cellule initiale est choisie comme
carrée. Une fois cette conformation adoptée, les
paramètres géométriques cellulaires, épaisseur
pariétale (e) et diamètre tangentiel
(D), sont fixés sous les trois contraintes suivantes
(Figure 3.8).
La masse volumique initiale , liée au facteur
de forme cellulaire e0/D (3.12) est choisie via un ensemble de profils
microdensitométriques pour être représentative du bois
initial (méthode de la moyenne décrite par Leban, 1999b). La
valeur retenue est
0.25 g/ cm3.
L'épaisseur pariétale initiale (eT = eR
= e0) doit répondre à des propositions bibliographiques
déjà présentées (valeur comprise au centre
d'un intervalle apte à rendre compte d'une variabilité intra
arbre, Guitard et al, 2002).
Le diamètre cellulaire tangentiel D est
calculé, puis sa valeur déduite est re- confrontée
à des références bibliographiques (Boyd, 1974).
Les caractéristiques de chaque type de cellule sont donc
:
Pour la cellule dite de bois initial :
épaisseurs radiale et tangentielle non distinctes et fixées
à
e0 =1 um, diamètre tangentiel fixé à D =23
um, facteur de forme e0/D =0.04, diamètre radial
DR = D.
Pour la cellule dite de bois final :
épaisseurs radiale et tangentielle variables e, diamètre
tangentiel fixe D, diamètre radial DR variable.
77
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.9 : Modifications de la géométrie
tissulaire envisagées lors de la transition d'une cellule de bois
initial à une cellule de bois final
Dans cette simulation, le diamètre radial DR est
soumis à une décroissance linéaire : les bornes (DR
min =15 um et DR max = 23 um) de l'intervalle de variations sont conformes aux
valeurs rencontrées dans la littérature (dont quelques exemples
ont été donnés dans le Tableau
2.3 du chapitre 2), le pas de variations est
déterminé en fonction des bornes précédemment
définies et du nombre de relevés
microdensitométriques disponibles (245 valeurs relevées tous
les 24um). La valeur du pas de variations de DR est donc directement obtenue en
divisant
l'écart entre les extrema (valeurs bornes) par
le nombre de relevés microdensitométriques. Une telle
procédure permet d'éviter une transition abrupte d'un bois
initial à un bois final conformément à des
constatations anatomiques (passage progressif du bois initial au bois final sur
ce résineux, Venet et al, 1986).
Moyennant les hypothèses précédentes, la
relation (2.13) du chapitre 2 devient (3.16) :
ñ e
e 2e 2
(3.16)
= +
2ñ m
D R
D D.D R
Posant
ñ
A = , cette dernière expression
devient :
2ñ m
2
2
A.D R .D = e.D + e.D R 2e
En posant de plus B tel que : A.D = B, l'unique
solution (biologiquement acceptable) de
l'équation du second degré (3.16) est alors
exprimée selon (3.17) :
(3.17)
e1 =
(D + D R ) +
(D + D R )
4
8.B.D R
Le Tableau 3.5 résume ainsi pour quelques valeurs
remarquables de densité relevées
expérimentalement (microdensitométrie), les
diamètres radial DR et épaisseurs de paroi (e1) calculés,
ainsi que les différents coefficients d'anisotropie
géométriques aLR, aLT et aRT précédemment
définis (relations 3.4, 3.4 et 3.6).
La Figure 3.9 représente, de manière
plus exhaustive et ce pour chaque relevé
microdensitométrique, les variations des valeurs attribuées aux
paramètres diamètre radial et épaisseur de paroi en
fonction de la densité relevée.
78
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Tableau 3-5 : Simulation intra cerne de
l'évolution du diamètre radial et de l'épaisseur en
fonction de la densité sur l'Epicéa ; conséquences sur les
rapports d'anisotropie tissulaire
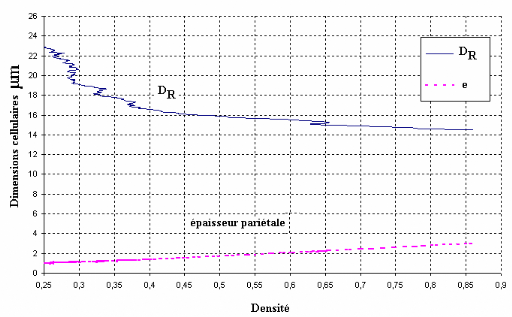
Figure 3.10 Variations simultanées des
paramètres diamètre radial et épaisseur de paroi dans le
cadre d'une simulation basée sur un relevé
microdensitométrique réalisé sur du bois adulte d'
Epicéa (Picea abies)
Une première remarque est que le rapport d'anisotropie
élastique L/T traduit par la valeur du coefficient aLT n'est toujours
pas de l'ordre de la valeur suggérée (L/T = 20) par
Guitard
(1987). L'allure générale des
évolutions (Tableau 3.5) des coefficients d'anisotropie
géométriques aLR, aLT et aRT avec la densité est
semblable à celle établie en ne faisant pas
varier l'épaisseur de paroi (paragraphe
précèdent). A une augmentation de la densité sont
simultanément associées une augmentation de
l'anisotropie L/R (facteur aLR) et une diminution de l'anisotropie
L/T (aLT).
79
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Une différence notable par rapport à la
précédente simulation (Figure 3.7) réside en
l'impossibilité d'une inversion de l'anisotropie
transverse (facteur aRT du Tableau 3.5) pour
la gamme de densité explorée (de 0,25 à
0,86). Cette dernière remarque montre le réalisme du
modèle ici décrit et alimenté par un jeu, en partie
expérimental, de données structurelles.
En second lieu, et ce conformément à des
propositions bibliographiques tirées d'examens microphotographiques
(Panshin et al, 1980), la Figure 3.9, comme le Tableau 3.5
font apparaître des variations relatives intra cerne d'épaisseurs
pariétales (e) plus importantes que celles du diamètre radial DR.
Dans la simulation analytique, si DR décroît de 23 um à 14
um, l'épaisseur pariétale varie du simple au triple (de 1
à 3 um). Les sens de variations avec la densité intra cerne
des paramètres géométriques cellulaires
diamètres et épaisseurs, observables sur la Figure (3.9),
sont comparables aux résultats obtenus à partir des
données numériques fournis par J.M. Leban (INRA, Nancy, LERFORB,
ERQB) sur du bois adulte de
5 essences résineuses (Figures 3.11 3.12, 3.13,
mesures des paramètres DR, DT, par planimétrie et
relevés microdensitométriques par absorption des rayons X). Si,
conformément
à la littérature évoquée
précédemment, la diminution du diamètre radial DR
accompagnant la
transition d'une cellule de bois initial à une cellule de
bois final est relativement bien admise, l'épaisseur de paroi ne peut
être considérée comme un paramètre constant.
Ces deux variations simultanées de
diamètre radial et d'épaisseur doivent donc
être hiérarchisées afin d'évaluer les
modifications des coefficients d'anisotropie géométriques
(rapportées dans le Tableau 3.5) accompagnant le
passage d'un bois initial à un bois final. Une simulation est
tentée (Tableau 3.6) avec, dans le cas 1, pour une cellule de bois
initial, une variation du diamètre DR à épaisseur
de paroi e fixée, tandis que dans le cas 2, seule
l'épaisseur e varie de 1 um à 3 um. Dans les deux cas les valeurs
bornes de chaque paramètre sont issues du Tableau 3.5.
La première partie du Tableau 3.6 (cas 1) montre les
évolutions des différents rapports avec une diminution de DR
(valeurs bornes tirées de la simulation) à épaisseur de
paroi constante. Ces résultats sont conformes aux évolutions des
différents facteurs d'anisotropie aLR, aLT et aRT, rapportées
sur la Figure 3.7.
La seconde partie (cas 2, Tableau 3.6) montre les variations des
mêmes rapports d'anisotropie aLR, aLT et aRT avec une augmentation de
l'épaisseur à diamètre radial DR constant.
On remarque que les rapports d'anisotropies aLT et aRT
évoluent dans le même sens pour les deux modifications
géométriques cellulaires envisagées, ceci
conformément aux résultats plus généraux de la
simulation intra cerne (diminution des rapports aLT et
aRT).
Pour le rapport aLR, les évolutions
sont différentes suivant la modification géométrique
envisagée (à épaisseur constante, une diminution
du paramètre DR conduit à une augmentation de
aLR tandis qu'une augmentation d'épaisseur de paroi,
à diamètre constant, entraîne une diminution de ce
même facteur). Une comparaison avec l'évolution intra cerne
du rapport d'anisotropie aLR (augmentation lors du
passage d'un bois initial à un bois final) rapporté dans le
Tableau 3.5 confirme que la diminution de diamètre radial constitue,
dans notre modélisation, la première modification
géométrique explicative de l'augmentation de
l'anisotropie L/R.
80
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
|
Densité
|
D (um)
|
DR
(um)
|
e (um)
|
aLR
|
aLT
|
aRT
|
|
Cas 1
|
|
|
|
|
|
|
|
|
0,25
|
22,92
|
22,92
|
1
|
1,91
|
13,85
|
7,24
|
|
0,28
|
22,92
|
18
|
1
|
2,16
|
6,44
|
3,79
|
|
0,35
|
22,92
|
15
|
1
|
2,39
|
3,92
|
2,5
|
|
|
|
|
|
|
|
|
|
Cas 2
|
0,25
|
22,92
|
22,92
|
1
|
1.91
|
13.85
|
7.24
|
|
0,48
|
22,92
|
22,92
|
2
|
1.83
|
3.93
|
2.15
|
|
0,69
|
22,92
|
22,92
|
3
|
1.74
|
2.38
|
1.37
|
Tableau 3-6 : Simulation de l'impact des modifications
univoques de l'épaisseur pariétale et du
diamètre
radial sur l'anisotropie élastique
tissulaire
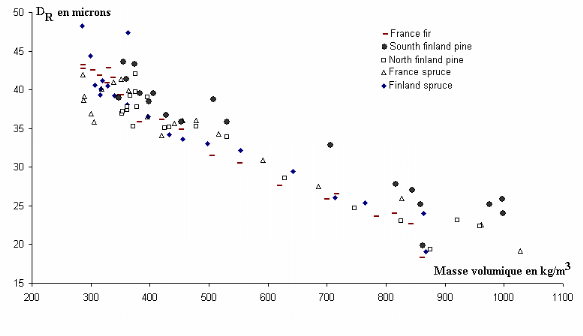
Figure 3.11 Evolutions intra cerne du diamètre
radial pour différentes essences résineuses

Figure 3.12 Evolutions intra cerne du diamètre
tangentiel pour différentes essences résineuses
81
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.13 Evolutions intra cerne de l'épaisseur
pariétale pour différentes essences résineuses
| 


