Section II : Critère de jugement de la
qualité de l'ajustement du modèle.
Question : Quelle est la qualité
d'ajustement de l'équation de la régression estimée? En
quelle mesure arrive-t-elle à expliquer les variations de la variable
dépendante?
Comme pour le modèle de régression multiple, on a
la décomposition suivante :
SCT = SCR + SCE avec SCT, la somme des carrées totales
ou variabilités totales de PIBt, SCE, somme des carrés
expliquée ou variabilité expliquée par le PIBt, SCR est la
somme des carrés des résidus ou variabilité des
résidus.
D'où
Comme pour le modèle de régression multiple on va
construire le critère du R2 á partir de
l'équation d'analyse de la variance, d'où
?
Le R2 ne permet de comparer que des modèles
ayant le même nombre de variable explicative, le même nombre
d'observation et la même forme.
Lorsque l'on ajoute des variables explicatives dans un
modèle, le R2 a tendance à augmenter sans qu'il y ait
forcement amélioration du modèle. C'est pourquoi lorsqu'on veut
comparer des
modèles qui n'ont pas le même nombre de variables
explicatives, on utilise le corrigé pour
s'affranchir du biais.
D'où 2 corrigé = 1-
Règle de décision :
Plus la SCE est proche de SCT, meilleur est l'ajustement du
nuage de points par la droite des MCO.
Le R2 est compris entre 0 et 1 : plus il est proche de
1, meilleur est l'ajustement.
Etant donné que le R2 est proche de 1,
l'ajustement est meilleur. Donc l'ensemble des quatre variables explicatives
influencent le phénomène sous études à 91.1524%.
A noter que le R2-carré ne peut être
interprété comme mesure de la signification statistique de la
relation estimée entre les X et Y. Une telle conclusion devra être
fondée sur des considérations qui impliquent la taille de
l'échantillon et les propriétés d'échantillonnage
de l'estimateur des MCO.
Tout comme le PIB, les paramètres estimés f30,
f31,f32, f33 et f34 sont des variables aléatoires qui varient d'un
échantillon à l'autre et possèdent donc une distribution
d'échantillonnage permettant
49
le développement des méthodes
inférentielles. Ainsi nous passons maintenant à
l'inférence statistique c'est-à-dire les tests d'hypothèse
basés sur des raisonnements probabilistes.
3.2.1. Test de significativité des
coefficients
Les différents tests statistiques sont importants dans
un travail économétrique car ils permettent de confirmer ou
d'infirmer la validité du modèle, et de voir le pouvoir
explicatif de chaque variable exogène. Ces tests sont utilisés
pour vérifier si, au cours de l'estimation, les hypothèses
classiques n'étaient pas violées car la violation de certaines
hypothèses fait perdre aux paramètres estimés certaines
qualités de bons estimateurs. Ainsi, dans le cadre de ce travail nous
nous recourons à un ensemble de tests.
3.2.1.1. Test de student
Pour savoir si une variable joue un rôle explicatif dans
un modèle, on effectue un test de student ou test de
significativité du coefficient de la variable explicative. Pour faire un
test de student, il faut vérifier au préalable que les erreurs
suivent une loi normale.
Soit H6: ìt N (0,
ó2) Laplace Gauss hypothèse de normalité des
erreurs.
Tout d'abord appliquons le test de normalité de des
résidus de Jarque-Bera.
3.2.2. Test de normalité de résidus de
Jarque-Bera
Pour savoir si les erreurs sont distribuées de
manière asymptotiquement normale, nous introduisons dans ce travail le
test de Jarque-Bera (1982). Ce dernier est fondé sur la
notion de Skewness (asymétrie) et de Kurtosis (aplatissement), qui
doivent être respectivement proches de 0 et de 3 dans le cas normal,
permet de vérifier une distribution statistique. Les tests de cette
spécification ont été effectués pour le
résidu du système (c'est-à-dire l'ensemble du
modèle). La statistique est la suivante :
La notion du Skewness et Kurtosis
P1= coefficient d'asymétrie (Skewness)
P2= coefficient d'aplatissement Kurtosis
Si la distribution est normale et le nombre d'observation grand
(n>30)
P1--* N (0 : et P2--*
On construit alors les statistiques :
v1= |P1 -0|/ et v2=|P2-3|/ que l'on compare
á 1.96 (valeur de la loi normale au
seuil de 5%).
50
Si les hypothèses H0 : V1=0 (symétrie) et v2=0
(aplatissement normal) sont vérifiées, alors V1 1.96 et v2 ; dans
le cas contraire, l'hypothèse de normalité est rejetée
B) test de normalité de résidus de
Jarque-Bera
Il s'agit d'un test qui synthétise les résultats
précédents ; si f31 et f32 obéissent à des lois
normales alors la quantité s : s= n/6
â1+n/24(â2-3)2 suit un X2 á deux
degré de liberté.
La forme quadratique associée permet de produire la
statistique de Jarque-Bera JB qui s'écrit :
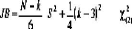
Avec n = Nombre d'observations
k = Nombre de variables explicatives si les données
proviennent des résidus d'une régression
linéaire. Sinon, k=0.
S =Coefficient d'asymétrie de l'échantillon
testé.
K = Kurtosis de l'échantillon testé.
Elle est distribuée asymptotiquement selon une loi du
÷2 1-á à 2 degrés de liberté. La statistique
JB
prend des valeurs d'autant plus élevées que
l'écart entre la distribution empirique et la loi normale
est manifeste.
Hypothèses du test :
H0 : les données suivent une loi normale.
H1 : les données ne suivent pas une loi normale.
Règle de décision : On rejette l'hypothèse
de la normalité si JB> ÷21-á(2),
÷2
1-á(2) = 5.99 au seuil critique de 5 %), sinon on accepte
l'hypothèse.
Ces tests de normalité servent également dans le
cas où il y a hétéroscédasticité. En effet,
l'hétéroscédasticité se manifeste sur le graphe de
la distribution par des queues de probabilité plus épaisses
(distribution leptokurtique) que les queues de la loi normale.
Règle de décision : Si la
probabilité associée au test de Jarque-Bera est supérieure
au seuil critique (5% habituellement), on rejette l'hypothèse de
normalité des erreurs en ce qui concerne la symétrie et
l'aplatissement de la distribution(H0), cela est conforme à la
statistique de Jarque-Bera et on accepte H1.
Par contre, si la probabilité est inférieure, on
accepte H1 en rejetant H0.
Eviews fournit la statistique de JB directement
JB = 1.445788
51
Analyse des résultats du test de
Jarque-Bera
D'après les règles de décisions du test,
nous pouvons dire que les erreurs sont normalement
distribuées, car la probabilité associée
à Jarque-Bera Pr (JB) = 0.485346 ? 0.05
3.2.3. Test de spécification : Test RESET
de RAMSEY
Le test de spécification de Ramsey RESET repose sur la
même idée simplificatrice que la forme
spéciale du test White. Au lieu d'inclure toutes les
spécifications possibles des variables
explicatives, on teste la significativité de fonctions
de la variable simulée .
Ce test consiste à tester s'il y a manque de variables
ou problème de formes fonctionnelles dans
notre modèle.
Les procédures se font en trois (3) étapes :
Estimation de la forme linéaire :
y=â0+â1X1+...+âkXk+U
Simulation de la variable prédite
Estimation de la forme linéaire :
y=â0+â1X1+...+âkXk+ó 2 +ó
3+v
Les hypothèses sont :
H0 : le modèle est bien
spécifié
H1 : le modèle est mal
spécifié
On accepte H0 si la valeur de la
probabilité associée au test de Ramsey est supérieure
à 5%
(seuil que l'on travaille), dans le cas contraire, on accepte
H1.
|
RAMSEY RESET Test :
|
|
F-statistic
|
0.821750
|
Probabilité
|
0.3825
|
|
Likelihood ratio
|
1.192253
|
Probabilité
|
0.2749
|
Analyse du test de RAMSEY RESET
Suivant les règles de décision du test, H0
est acceptée au risque de 5% de se tromper, on peut conclure que le
modèle est bien spécifié, ce qui signifie qu'il n'y a pas
manque de variables ni problème de forme fonctionnelle dans notre
modèle.
3.2.4. Test de la stabilité des
coefficients ou de Grégory CHOW
Lorsqu'on utilise un modèle en séries
temporelles, des changements structurels peuvent se produire entre la variable
à expliquer et les variables explicatives : les paramètres ne
restent pas globalement identiques sur toute la période. En effet,
comment détecter un changement structurel ? Pour détecter un
changement structurel dans un tel model, on fait appel à un test
appelé Test de Grégory CHOW.
52
Ce test, a été élaboré par
Grégory CHOW, pour stabiliser un modèle
économétrique. Le test de
CHOW estime deux modèles en utilisant l'ensemble des
données et un autre utilisant une période
restreinte. Ce test nous permet de répondre à la
question suivante. Peut-on considérer le modèle
comme étant stable sur la totalité de la
période ou bien doit-on considérer deux périodes
distinctes d'estimation ?
Etape 1 : En effet, pour effectuer ce test,
les étapes suivantes doivent être suivies
H0: SCR = SCR1 + SCR2, le
modèle est stable
H1: SCR ? SCR1 + SCR2, le
modèle est instable
Etape 2
On divise la taille de l'échantillon en deux
sous-périodes
T = T1 + T2, puis on estime le modèle sur T1
et T2 et on calcule SCR1 et SCR2
Ainsi, le travail à faire c'est de chercher s'il existe
une différence explicative entre la somme des
carrés des résidus du modèle
estimés sur l'ensemble de la période T et l'addition de la
somme
des carrés du résidu calculé à
partir de deux sous-période.
Règle de décision :
Les coefficients du modèle sont stables si la
probabilité est supérieure à 5%, tandis que les
coefficients du modèle sont instables si la
probabilité est inférieure à 5%.
Les résultats de ce test en utilisant le
logiciel EVIEWS nous donnent :
Chow Breakpoint Test: 2007
Null Hypothesis: No breaks at specified breakpoints Varying
regressors: All equation variables
Equation Sample: 1996 2013
|
F-statistic
|
1.310169
|
Prob. F(5,8)
|
0.3489
|
|
Log likelihood ratio
|
10.76773
|
Prob. Chi-Square(5)
|
0.0562
|
|
Wald Statistic
|
6.550844
|
Prob. Chi-Square(5)
|
0.2562
|
Analyse du test de CHOW
Selon la règle de décision attribuée au test
de Gregory CHOW, l'une des deux probabilités étant
Null Hypothesis: No breaks at specfied breakpoints Vyng regr All
eq bs
donc inférieures à 5%, on accepte
H0, et on conclut que les coefficients du modèle sont
stables.
Equaion Sample 996 2013
53
Testons chaque paramètre du modèle
:
Tout d'abord les étapes du test de
student
Etape 1 : Hypothèse
H0 : ai ? 0 avec i=1,2..., (k-1) --le coefficient est
significatif
H1 : ai = 0 --le coefficient n'est pas significatif
Tout en choisissant un seuil critique, soit á = 5% et
ttab=2.145
Etape 2 : La statistique de test est la suivante
:
--S(T-K)
La statistique de test suit une loi de student à T-k
degrés de liberté car les erreurs du modèle suivent une
loi normale.
Sous H0 vraie, on a -- S(T-k)
Etape 3 : La règle de décision est
la suivante :
-Si ItcalculéI>ttab où
ttab est la valeur critique de la table de student pour un risque
fixé et un
nombre de degré de liberté égal à
(T-K)
On rejette H0 et on accepte H1 c'est-à-dire le coefficient
est significativement différent de zéro et
la variable joue un rôle explicatif dans le
modèle.
-Si ItcalculéI<ttab on accepte H0 et on rejette H1
Pour Test du paramètre â0 :
En regardant les résultats de l'estimation du
modèle, nous voyons la valeur calculée de Student
ainsi que sa probabilité pour le paramètre f30,
à savoir pour la constante C.
ItcalculéI= 2.724993 et Prob(tf30)= 0.0173 á =
5%
2.724993. Etant donné que ItcalculéI>ttab, 0n
rejette H0 donc le paramètre f30 est
statistiquement non significatif pour á= 5%.
Pour test du paramètre â1
ItcalculéI= 1.985274 et Prob(tf31)= 0,0686 et á=
5%
. ItcalculéI< ttab, nous acceptons H0. Donc le
paramètre f31est statistiquement
significatif pour á= 5%.
Pour test du paramètre â2
ItcalculéI=4.290471 et Prob(tf32)= 0.0009 et á =
5%
, Etant donné que ItcalculéI>ttab, 0n rejette
H0 donc le paramètre f32 est
statistiquement non significatif pour á= 5%.
54
Pour test du paramètre f3
tcalculé= 0.773956 et Prob(tf33)= 0.4528 et á =
5%
, tcalculé< ttab, nous acceptons H0. Donc le
paramètre f33 est statistiquement
significatif pour á= 5%.
Pour test du paramètre f4
tcalculé= -3.688064 et Prob(tf34)= 0.0027 et á =
5%
, tcalculé< ttab, nous acceptons H0. Donc le
paramètre f34 est statistiquement
significatif pour á= 5%.
Intervalle de confiance sur les
paramètres
L'intervalle de confiance (IC) est un intervalle de valeur qui
a un pourcentage de chance de contenir la vraie valeur du paramètre
estimé. Avec moins de rigueur, il est possible de dire que l'IC
représente la fourchette de valeurs à l'intérieur de
laquelle nous sommes certains que ce pourcentage représente la vraie
valeur recherchée. L'intervalle de confiance est donc l'ensemble des
valeurs raisonnablement compatibles avec le résultat observé
(l'estimation ponctuelle). Il donne une visualisation de l'incertitude de
l'estimation. Des intervalles de confiances à 99% ou à 90% sont
parfois utilisés. La probabilité (degré de confiance) de
ces intervalles de contenir la vraie valeur est respectivement 99%, 95% et 90%.
Dans notre cas, nous avons utilisé le seuil critique de 5% pour calculer
l'intervalle de confiance.
Coefficient Confidence Intervals Date: 11/05/16 Time: 09:31
Sample: 1996 2013
|
Included observations: 18
|
|
|
|
|
|
95% CI
|
|
Variable
|
Coefficient
|
Low
|
High
|
|
C
|
4.977073
|
1.031261
|
8.922885
|
|
TSP
|
0.239599
|
-0.021132
|
0.500329
|
|
M
|
0.637710
|
0.316605
|
0.958814
|
|
IDOL
|
0.248462
|
-0.445078
|
0.942002
|
|
TXCHNG
|
-0.028333
|
-0.044929
|
-0.011736
|
55
P0 à l'intervalle [1.031261, 8.922885] ;
nous avons donc un risque de 5% que le véritable coefficient P0
se trouve à l'intérieur de cet intervalle.
P1 se trouve dans l'intervalle [-0.021132,
0.500329] ; on peut faire confiance à 95% que le véritable
coefficient de P1 se trouve à l'intérieur de cet
intervalle.
P2 appartient à l'intervalle [0.316605,
0.958814] ; au risque de 5%, nous pouvons conclure que le véritable
coefficient P2 se trouve à l'intérieur de cet
intervalle.
P3 se trouve dans l'intervalle [-0.445078,
0.942002] ; au seuil critique de 5%, nous pouvons conclure que le
véritable coefficient de P3 appartient à cet
intervalle.
P4 se trouve dans l'intervalle [-0.044929,
-0.011736] ; le véritable coefficient de P4 se trouve
à
l'intérieur de cet intervalle, toutefois, nous avons le
risque de 5% de se tromper.
A la lecture de ces résultats, nous pouvons conclure qu'il
y'a 95% de chance pour que les
soient les vraies valeurs de P0, P1, P2, P3 et
P4
3.2.1.2. Test de Fisher- Snedecor
Le test de Fisher permet de tester la significativité de
l'ensemble des coefficients du modèle.
Etape 1 : Les hypothèses du test de Fisher sont
les suivantes :
H0 : â1=â2 =......=ak-1=0 (la
constante â0 est non nul). L'ensemble des coefficients du modèle
est
non significatif
H1 : il existe au moins un coefficient non
nul.
La statistique de test sous H0 vraie est :
F* = (R2/ K) ? F* =
44.78567
[(1-R2)/(T-K- 1)]
Etape 2 : Règle de décision
-Si F* on accepte H0 et on rejette H1, le
modèle est globalement significatif.
Si F* on rejette H0 et on accepte H1 le modèle
n'est pas globalement significatif.
á = 5%, V2 = T-K- 1 alors V2 = 18-4-1= 13
V1 = K-K' ? V1 = 4-1, V1 = 3
Ftab = 3.41
Etant donné que F* est supérieur à
Ftab, nous acceptons H0, donc nous pouvons dire que le
modèle est globalement significatif.
3.2.5. Test de Multi colinéarité «
Test de Klein »
Le test de Klein est fondé sur la comparaison du
coefficient de détermination calculé sur le
modèle à k variables explicatives
56
Et les coefficients de corrélation simple entre les
variables explicatives pour i ? j.
Règle de décision
Si , il y a presomption de multicolinéarité.
Dans le cas contraire il n'y aura pas de risque de multi
colinéarité
Il ne s'agit pas d'un test statistique au sens d'un test
d'hypothèses mais simplement d'un critère de présomption
de multi colinéarité.
Les résultats de l'estimation sont les suivants :
LPIB=4.977073+0.239599LTSP+0.637710LM+0.248462IDOL-0.028333txCHNG
(2.724993), (1.985274), (4.290471), (0.773956), (-3.688064)
(
): Sont les T student.
n = 18 R2 =0.932342
Les coefficients de corrélations simples d'après le
logiciel Eviews sont : r2 x1 x2 = 0.935608 r2 x1 x3= -0.579071 r2 x1
x4=0.933987
r2x2 x3=-0.507809
r2x2x4=0.833077 r2x3
x4=-0.456956
À la lecture de ces coefficients, il semble que notre
modèle est frappé de multi colinéarité puisque les
coefficients de corrélation liés aux transferts sans contre parti
et l'importation, soit r2 x1 x2=0.935608 et les
coefficients de corrélation liés aux transferts sans contrepartie
et le taux de change, soit r2 x1 x4=0.933987 sont
supérieurs du coefficient de détermination. A cet effet, nous
allons procéder à un autre test qui est celui de Farrar-Glauber
pour pouvoir conclure s'il y a multi colinéarité ou non.
3.2.6. Test de Farrar -Glauber
Le test de Farrar et Glauber est utilisé pour
détecter l'éventualité d'une multi
colinéarité. Ce test permet de mesurer l'importance de la multi
colinéarité, sa structure, et donc sa localisation. Il comprend
les étapes suivantes :
Etape 1 : on établit la matrice des
coefficients de corrélation des variables explicatives :
57
1
1
1
Lorsque la valeur du déterminant D tend vers zéro
le risque de multi colinéarité est important. Etape 2
: les hypothèses du test sont les suivantes :
H0 = |D| = 1 les séries sont orthogonales H1 =
|D| < 1 les séries sont déterminantes Etape 3
: La deuxième étape consiste à calculer le
déterminant de la matrice des coefficients de corrélation entre
les variables explicatives :
D =
Lorsque la valeur du déterminant D tend vers
Zéro, le risque de multi colinéarité est important. Calcul
du déterminant de la matrice
2
D =
D =0.008215
Etape 4 : la quatrième étape
consiste à effectuer un test du X2, en posant les
hypothèses ci-
dessus.
H0 : D=1 (Les séries sont orthogonales)
H1 : D?1 (Les séries sont dépendantes)
La valeur empirique du X2 est :
* ÷
= - [n - 1- (1/6) (2 K + 5)] ln D
n : taille de l'échantillon
K : nombre de variable explicative
(terme constant inclus, K = k + 1)
58
Ln : logarithme
népérien
= - [18 - 1- (1/6) (2 × 5 + 5)] ln 0.008215
=68.02541
Cette valeur est à comparer à la valeur lue dans la
table : ddl à Y2 K (K-1) = Y2. 5(5-1) = 10 pour un seuil á = 0.05
= 18.307
Etape 5 : Règle de décision
Si X2 X2 tab. On rejette H0 on dit qu'il y a multi
colinéarité
Si X2< X2 tab. On accepte H0 et on conclut qu'il n'y a pas
présomption de multi colinéarité.
Puisque > nous rejetons l'hypothèse H0, il y a
présomption de multi colinéarité entre les
variables explicatives dans le modèle.
Ces deux tests conduisent donc à des résultats
différents, cependant le test de Farrar et Glauber,
dont le fondement théorique est plus affirmé,
semble devoir être privilégié.
Correction de la multi colinéarité
Afin d'apporter des solutions au problème de multi
colinéarité, deux méthodologies peuvent être
adopté :
L'augmentation de la taille de l'échantillon.
La Ridge Regression
Afin de corriger la multi colinéarité de notre
modèle économétrique, nous avons choisis
d'adopter la deuxième méthode.
La Ridge Régression est une réponse purement
numérique. Il s'agit de transformer la matrice
X'X en (X'X + cI) où c'est une constante choisie
arbitrairement qui, en augmentant les valeurs
de la première diagonale, réduit les effets «
numériques » de la multi colinéarité.
Nous allons transformer la matrice X'X en (X'X+cI),
où c'est une scalaire arbitraire (c = 2 dans
notre cas). Ainsi, on arrivera à réduire les effets
numériques de la multi colinéarité.
D'abord, nous allons déterminer (X'X +
cI)-1, ensuite nous calculerons â = (X'X +
cI)-1 X'Y
D'après les calculs, on a trouvé les
résultats suivants :
D'o â = (2.488536; 0.239599 ; 0.637710 ; 0.248462
;-0.028333)
Ainsi le modèle estimé à nouveau
s'écrit de la façon suivante:
Y= 2.488536+0.239599 LTSP1t+0.637710 LM2t+0.248462
IDOL3t-0.028333txCHNG4t
59
Détection de l'autocorrélation des
erreurs
Le phénomène d'autocorrélation des
erreurs est issu de la violation de l'hypothèse H4. En effet, il y a
auto corrélation des lorsque les erreurs sont liées par un
processus de reproduction. L'auto-corrélation peut être
observée pour plusieurs raisons:
L'absence d'une variable explicative importante dont
l'explication résiduelle permettrait de blanchir les erreurs.
Une mauvaise spécification du modèle, les
relations entre la variable à expliquer et les variables explicatives ne
sont pas linéaires et s'exprimant sur une autre forme que celle du
modèle exprimé (logarithme, différences premières
etc....).
Un lissage par moyenne mobile ou une interpolation des
données créer une auto corrélation artificielle des
erreurs dues à l'usage de ses deux opérateurs.
L'auto- corrélation des erreurs se rencontre
essentiellement dans les modèles en série temporelle où
l'influence d'une erreur due à une mauvaise spécification d'une
période sur l'autre est plausible.
Au fait, nous allons utiliser le test de DURBIN-WATSON (DW)
pour pourvoir détecté s'il y a auto corrélation des
erreurs dans notre modèle.
3.2.7. Test de Durbin et Watson
Etape 1 : Le test de Durbin et Watson (DW)
permet de détecter l'auto corrélation des erreurs d'ordre 1 selon
la forme
Etape 2 : Le test d'hypothèses est le
suivant :
H0 : ñ = 0
H1 : ñ ? 0
Pour tester l'hypothèse nulle H0, nous calculons la
statistique de Durbin et Watson :
DW =Ó (Ût - Ût-1)2
ÓÛ2 t
Conditions d'utilisation de ce test :
-Le modèle doit comporter impérativement un
terme constant.
-La variable à expliquer ne doit pas figurer parmi les
variables explicatives(en tant que variable
retardée), il faut alors recourir à la
statistique h de Durbin.
60
-Pour les modèles en coupe instantanée, les
observations doivent être ordonnées en fonction des
valeurs croissantes ou décroissantes de la variable
à expliquer ou d'une variable explicative
soupçonnée être la cause de l'auto
corrélation.
-Le nombre d'observations doit être supérieur ou
égal à 15
-Le test de Durbin et Watson est un test présomptif
d'indépendance des erreurs du fait qu'il
utilise les résidus ; de plus, il ne test qu'une auto
corrélation d'ordre 1.
Règle de décision :
Selon la position du DW empirique dans cet espace, nous pouvons
conclure :
Si d2< *DW < 4-d2, on accepte l'hypothèse H0 -
ñ = 0 ; (pas d'auto corrélation).
Si 0 < *DW < d1, on rejette l'hypothèse H0 -
ñ > 0 ; (auto corrélation positive)
Si 4 - d1< *DW< 4, on rejette l'hypothèse H0 -
ñ < ; 0 (auto corrélation négative).
Si d1< *DW < d2 ou 4 -d2< *DW < 4 -d1, il y a
doute.
Sachant que : á= 5%, d1=0.82 d2= 1.87 k=4 DW=
1.369286
d1<DW<d2 la valeur de DW se situe dans la zone de
l'incertitude, cependant à proximité immédiate de la zone
d'acceptation de H0, nous pouvons conclure à une absence d'auto
corrélation des résidus.
Graphique de l'autocorrélation des erreurs
3.2.8. Test de Breusch-Godfrey
Ce test est un test de stabilité sur les erreurs. Il
est important parce qu'il permet de remplir l'une des conditions de la
validité des résultats de la Méthode des MCO
(Méthode que nous avons utilisé dans l'étude pour la
régression) ; cette condition est la non corrélation
sérielle des résidus. Nous utilisons à cet effet, le test
de Breusch-Goldfrey ; il consiste à tester l'hypothèse nulle
H0 (les résidus ne présentent pas de
corrélation sérielle) conte l'hypothèse alternative
H1 (les résidus présentent de corrélation
sérielle).
?, la statistique de BG, par définition tend vers une
loi Khi deux à h degré de liberté (ddl), avec h le nombre
de retard. Mathématiquement, cela s'écrit :
?~÷2(h).
La décision suivante en découle selon le
résultat obtenu.
61
Si ?<÷2(h), alors nous
acceptons l'hypothèse nulle H0 et les résidus ne
présentent pas une corrélation sérielle ; dans ce cas, les
résultats données par la méthode des MCO sont
validées. Si ?>÷2(h), alors nous
rejetons l'hypothèse nulle H0 et les résidus
présentent une corrélation Sérielle ; alors les
résultats données par la Méthode des MCO ne peuvent
être validées.
|
Breusch-Godfrey Serial Correlation LM Test:
|
|
F-statistic
|
1.145039
|
Probabilité
|
0.3534
|
|
Obs*R-squared
|
3.101667
|
Probabilité
|
0.2121
|
Analyse du test de non auto corrélation de
Beusch-Godfrey
Les valeurs des deux probabilités étant
supérieures à 5%, dans ce cas H0 est
acceptée, à savoir les erreurs sont non auto
corrélés entre elles à 95% de confiance.
Test D'HETEROCEDASTICITE
L'hétéroscédasticité qualifie des
données qui n'ont pas une variance constante. En effet,
l'hétéroscédasticité ne biaise pas l'estimation des
coefficients, mais l'inférence habituelle n'est plus valide puisque les
écarts-types trouvés ne sont pas les bons.
Ils existent plusieurs tests qui se ressemblant pour
détecter l'hétéroscédasticité dont le test
de Breusch- Pagan dont l'hypothèse H0 est que tous les coefficients de
la régression des résidus au carré sont nuls,
c'est-à-dire que : les variables du modèle n'expliquent pas la
variance observée. Si le <<p-value>> est
inférieur au seuil de significativité (1%, 5%, 10%), on rejette
l'hypothèse nulle.
3.2.9. Test de Breusch-
Pagan-Godfrey
Heteroskedasticity Test: Breusch-Pagan-Godfrey
F-statistic 0.266735 Prob. F(4,13) 0.8941
Obs*R-squared 1.365251 Prob. Chi-Square(4) 0.8502
Scaled explained SS 0.620047 Prob. Chi-Square(4) 0.9608
Les résultats issus de l'estimation sous eviews nous
montrent que les erreurs sont homoscédastiques puisque la
probabilité affichée est supérieure à 5%.
Précédemment, on a pu constater que le
modèle explique la réalité à 93.2342%. À
présent, nous allons apprécier le caractère
prévisible du modèle. A cet effet, nous allons confronter les
données statistiques de la réalité observée.
62
Validation du modèle (diagnostic,
prévision, simulation)
La dernière étape est celle de la validation du
modèle :
- Les relations spécifiées sont-elles valides ?
- Peut-on estimer avec suffisamment de précision les
coefficients ?
- Le modèle est-il vérifié sur la
totalité de la période ?
- Les coefficients sont-ils stables ?
Diagnostic :
Utilisons le modèle estime : Y = â1 X1 + â2 X2
+ â3 X3 + â4 X4+ ? en déterminant la dérivée
de Y
par rapport à X1, X2 , X3 et X4 pour trouver la
valeur des estimateurs â1, â2, â3 et â4.
Le modele estimé est :
E
Th=4.977073+0.239599LTSP+0.637710LM+0.248462IDOL-0.028333txCHNG
(2.724993), (1.985274), (4.290471), (0.773956), (-3.688064)
(
): Sont les T student.
n = 18 R2 =0.932342
DW*=1.369286
Prévision pour un niveau donne de X
Présenter un modèle économétrique,
cela doit permettre de faire des prévisisons sur les valeurs futures de
la variable expliquée.
Le principe demeure le même que pour la régression
simple. On veut savoir quelle est la valeur future de la variable
endogène, si on connait la valeur future de la variable exogène,
avec un ensemble de variable exogène.
Soit le modèle suivant : Yt+2 = â0 +
â1Õ1+2 + â2Õ2+2 +â3Õ3+2
+â4Õ4+2
Estimation ponctuelle pour un niveau de X donne, X=Xp
La prévision de la valeur individuelle de y pour un niveau
de X donne est la même que la prévision de la moyenne
conditionnelle de Y étant donne X=Xp.
Yt+2 =Yt +ÄYt X1+2 =X1 + ÄX1 X2+2 =
X2 + ÄX2 X3+2 = X3 + ÄX3 X4+2 = X4 + ÄX4 Donc, il
s'agit de déterminer la valeur future du Produit Intérieur Brut
de l'année 2015, 2016, 20017et 20018 considérant que les
transferts privés, les importations, l'indice de dollarisation et le
taux de change varient au cours de ces quatre périodes.
63
Faisons une prévision pour un horizon de quatre
années suivantes, c'est-à-dire 2015, 2016, 2017
et 2018
Soit le modèle :
=4.977073+0.239599LTSP+0.637710LM+0.248462IDOL-0.028333txCHNG
Calculons la variation moyenne de X1, X2 X3 et X4 selon la
formule suivante :
4Xi= n .
En remplaçant les variables par leur valeur, nous avons
comme résultats :
4X1= s 4X2=
008323
4X3= -- 1 * 4X4=
Pour l'année 2015 on a : Compte tenu des
estimations :
|
X1+2
|
=
|
20.98533
|
(1+0.36941)2 = 39.3534
|
|
X2+2
|
=
|
21.99054
|
(1+ 0.31549)2 =38.0549
|
|
X3+2
|
=
|
0.008323
|
(1+0.61405)2 =0.0144
|
|
X4+2
|
=43.73
|
(1+0.69196)2=125.1871
|
En revenant dans l'équation initiale, on a :
2015=4.977073+0.239599*39.3534+0.637710*38.0549+0.248462*0.0144-0.028333*125.1871
2015=35.13077
Donc, pour l'annee 2015, le PIB reel de l'économie
haitienne s'elevera à 35.13077 suivant la prévision du modele.
Il est important de souligner que cette valeur du PIB
est sous la forme logarithmique. Tandis que l'estimation ponctuelle
est la même qu'on cherche à prédire la valeur individuelle
de Y pour Xp ou la moyenne conditionnelle de Y étant donne Xp, le
calcul inférentiel sur les quatre variables n'est pas
identique. L'inférence sur la moyenne conditionnelle ne tient compte que
de l'erreur d'estimation sur les paramètres à estimer, tandis que
l'inférence sur une valeur individuelle de Y doit tenir compte en plus
de la variance Ut.
64
Estimation par intervalle de confiance
t+2
t+2 - óEp. tá/2T-K-1 t+2 +
óEp. tá/2T-K-1
Pour toute prévision, on doit avoir une marge d'erreur.
Ainsi, nous allons calculer l'erreur de prévision. La variance de cette
erreur est donnée par la formule suivante :
Var (Ep) = Ó / (T -K - 1) * [ * (X'X)-1
* + 1]
Var (Ep)= 0.016452
Et son écart-type est : óEp = ?
óEp =0.12826
Et l'intervalle de t+2 devient alors :
35.13077-0.12826*2.179 35.13077+0.12826*2.179
34.8513 35.4102
Pour l'année 2016 on a
: Compte tenu des estimations :
|
Õ1+3
|
=
|
20.98533
|
(1+0.36941)3 = 53.8910
|
|
Õ2+3
|
=
|
21.99054
|
(1+ 0.31549)3 =50.0608
|
|
Õ3+3
|
=
|
0.008323
|
(1+0.61405)3 =0.0349
|
|
Õ4+3
|
=43.73
|
(1+0.69196)3=211.8116
|
La nouvelle prévision du PIB pour l'année 2016
devient alors :
2016=4.977073+0.239599*53.8910+0.637710*50.0608+0.248462*0.0349-0.028333*211.8116
D'où 2016=43.8209
Donc, le PIB en l'année 2016 s'élèvent
à 43.8209 selon la prévision du modèle.
Intervalle de confiance
t+3 - óEp. tá/2T-K-1 t+3 +
óEp. tá/2T-K-1
43.8209-0.12826*2.179 43.8209+0.12826*2.179
43.3514 44.1003
Pour l'année 2017 on a
: Compte tenu des estimations :
|
Õ1+4
|
=
|
20.98533
|
(1+0.36941)4 = 73.7988
|
|
Õ2+4
|
=
|
21.99054
|
(1+ 0.31549)4 =65.5996
|
|
Õ3+4
|
=
|
0.008323
|
(1+0.61405)4=0.0564
|
65
X4+4 =43.73 (1+0.69196)4=358.3767
La nouvelle prévision du PI13 pour l'année 2017
devient alors :
2017=4.977073+0.239599*73.7988+0.637710*65.5996+0.248462*0.0564-0.028333*358.3767
D'où 2017=54.3528
Donc, le PI13 en l'année 2016 s'élèvent
à 54.3528 selon la prévision du modèle.
Intervalle de confiance
t+4 - óåp. tá/2T-K-1 t+4 +
óåp. tá/2T-K-1
54.3528-0.12826*2.179 54.3528+0.12826*2.179
54.0733 54.6322
Pour l'année 2018 on a
: Compte tenu des estimations :
|
X1+5
|
=
|
20.98533
|
(1+0.36941)5 = 101.0609
|
|
X3+5
|
=
|
21.99054
|
(1+ 0.31549)5 =86.6310
|
|
X4+5
|
=
|
0.008323
|
(1+0.61405)5=0.0911
|
|
X5+5
|
=43.73
|
(1+0.69196)5=606.3591
|
La nouvelle prévision du PI13 pour l'année 2018
devient alors :
2018=4.977073+0.239599*101.0609+0.637710*86.6310+0.248462*0.0911-0.028333*606.3591
D'où 2018=67.2792
Donc, le PI13 en l'année 2018 s'élèvent
à 67.2792 selon la prévision du modèle.
Intervalle de confiance
t+5 - óåp. ta/21,4(4
<
aJ2T-K1< PIB
t+5 + óåp. tá/2T-K-1
67.2792-0.12826*2.179 67.2792+0.12826*2.179
66.9997 67.5586
NB : rappelons que les valeurs prévisibles pour
les PIB sont en logarithme
66
| 


