CONCLUSION
L'objectif de ce travail était d'étudier la
performance prévisionnelle, hors échantillon, de plusieurs
modèles de taux de change fondés sur la valeur actualisée,
spécifiquement pour le taux de change USD/CAD. Les modèles
initiaux sont le modèle de Parité Ouvert des Taux
d'Intérêt (POTI), le modèle de Parité du Pouvoir
d'Achat (PPA), le Modèle financier (MF), le modèle avec Prix de
l'Énergie (PE) et un VAR. L'étude a été faite avec
des observations mensuelles, puis reprise avec des observations
trimestrielles.
Les modèles initiaux ont été
modifiés9 en différenciant les régresseurs pour
obtenir des variables stationnaires. La période d'étude est de
1976 à 2014. L'échantillon de de prévision est de 1986
à 2014. Les horizons de prévision sont de 1 à 12 mois
(fréquence mensuelle) et 1 à 4 trimestres (fréquence
trimestrielle). Les approches de prévision appliquées sont
l'approche récursive, les approches roulantes 5 ans et 10 ans.
Concernant la performance prévisionnelle des
modèles POTI, PPA, MF et PE modifiés par rapport à la
marche aléatoire, l'analyse des critères U de Theil, ÄREQM
et R E , conduit aux résultats communs suivants :
-avec la fréquence mensuelle et pour les horizons h=1,
2, 3, 4, 5, 6, 7, 8 et 12, les modèles MF et POTI modifiés font
mieux que la marche aléatoire. Ces modèles font pire sur les
horizons 9, 10 et 11. Quant aux modèles PPA et PE modifiés, il
battent la marche aléatoire sur les horizons h= 2, 3, 4, 5, 6, 7, 8 et
12, mais ils font pire sur
83
horizons 1, 9, 10 et 11. Cependant avec la fréquence
trimestrielle, les modèles font pire que la marche aléatoire
durant quelques années au début de tous les quatre horizons.
-Au début de l'échantillon de prévision
(1986-1991), l'approche roulante 5 ans est la meilleure pour les fré
quences mensuelle et trimestrielle. Pendant la seconde période
(1992-2014), c'est l'approche récursive qui est la meilleure pour les
deux fréquences. Quelque soit la période de l'échantillon,
le meilleur modèle pour la fréquence mensuelle est le
modèle MF. Pour la fréquence trimestrielle, le meilleur
modèle est le modèle POTI.
Quant à l'analyse des critères IPA et IPM, elle
indique que, pour tout l'échantillon de prévision (1986-2014),
l'approche récursive est la meilleure pour les deux fréquences
à la fois. De même durant cette période, le meilleur
modèle pour la fréquence mensuelle reste le modèle MF.
Tandis que c'est le modèle POTI qui s'impose toujours en
fréquence trimestrielle.
Dans l'ensemble de l'étude, la fréquence
mensuelle est celle qui permet d'obtenir les meilleures performances
prévisionnelles par rapport à la marche aléatoire. Avec
cette fréquence, les modèles POTI et MF battent la marche
aléatoire sur les horizons 1 à 8 et 12. En ce qui concerne les
modèles PPA et PE , ils performent le mieux sur les horizons 2 à
8 et 12.
APPENDICE A
RÉSULTATS DE L'ÉTUDE À LA FRÉQUENCE
MENSUELLE.
Variables
Tableau A.1
|
Coefficients de corrélation (fréquence
mensuelle)
|
|
P1
|
P4
|
P6
|
P12
|
|
-0.051
|
0.114
|
-0.075
|
0.052
|
|
0.848
|
0.393
|
0.310
|
0.041
|
|
0.982
|
0.918
|
0.875
|
0.724
|
|
0.980
|
0.910
|
0.848
|
0.612
|
|
0.868
|
0.612
|
0.466
|
-0.045
|
|
0.954
|
0.835
|
0.750
|
0.489
|
|
0.931
|
0.793
|
0.713
|
0.423
|
|
0.987
|
0.932
|
0.891
|
0.753
|
|
0.974
|
0.879
|
0.822
|
0.599
|
Tableau.A.2 Tests de racine unitaire et
stationnarité en différence première
(fréquence
mensuelle)
|
Variables
|
Nombre Adf-t
de retards
|
Kpss- résultat
|
|
0
|
-18.421
|
0.072
|
Stationnaire
|
|
11
|
-4.123
|
0.441
|
Stationnaire
|
|
16
|
-2.567
|
0.436
|
Stationnaire
|
|
9
|
-4.861
|
0.18
|
Stationnaire
|
|
11
|
-5.392
|
0.128
|
Stationnaire
|
|
11
|
-5.042
|
0.078
|
Stationnaire
|
|
0
|
-21.063
|
0.064
|
Stationnaire
|
|
0
|
-18.853
|
0.040
|
Stationnaire
|
La valeur critique du test ADF à 5% est -2.867/ La
valeur assymptotique critique du test KPSS est 0.463/ La deuxième
colonne indique le nombre de retards dans l'équation empirique pour le
test ADF

Tableau A.3 Indicateurs IPA et IPM
(fréquence mensuelle)
*POTI : Parité ouverte de taux de chage/ PPA :
Parité du pouvoir d'achat,/ MF : modèle financier; PE :
modèle avec prix de l'énergie/IPA : Indicateur de Performance par
Approche /IPM : Indicateur de Performance de Modèle
APPENDICE B
RÉSULTATS DE L'ÉTUDE À LA FRÉQUENCE
TRIMESTRIELLE
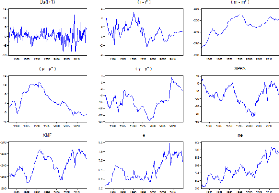
Figure B.1Graphiques des variables de
l'étude ( fréquence trimestrielle)
88
Tableau B.1 Statistiques
descriptives(fréquence trimestrielle)
|
Variables
|
Moy
|
Ecar-T
|
skew
|
Kurt
|
ñ1
|
ñ4
|
|
0.16
|
3.25
|
0.18
|
5.19
|
0.148
|
0.047
|
|
1.04
|
1.53
|
0.41
|
3.1
|
0.869
|
0.598
|
|
5.06
|
4.4
|
0.3
|
1.88
|
0.971
|
0.870
|
|
-222.94
|
14.32
|
-0.83
|
3.05
|
0.986
|
0.914
|
|
-11.55
|
6.15
|
0.29
|
2.62
|
0.973
|
0.832
|
|
-15.59
|
11.95
|
-0.49
|
2.51
|
0.957
|
0.809
|
|
-239.05
|
16.7
|
-0.09
|
1.78
|
0.969
|
0.834
|
|
6.51
|
0.57
|
0.49
|
2.03
|
0.953
|
0.817
|
|
5.49
|
0.27
|
0.57
|
2.47
|
0.966
|
0.851
|
Note : le nombre d'observations est : 156.
89
Tableau B.2 Tableau des Tests ADF et KPSS
à niveau (fréquence trimestrielle)
|
Variables
|
Lag
|
Adf-t
|
V.Addf
|
résul
|
Kpss-
|
V.
|
résultat
|
|
0
|
-10.35
|
0.00
|
Sta
|
0.18
|
0.46
|
St
|
|
4
|
-2.79
|
0.06
|
N.stb
|
0.51
|
0.46
|
N st
|
|
1
|
-0.96
|
0.77
|
N.st
|
0.697
|
0.46
|
N.st
|
|
3
|
-2.497
|
0.12
|
N.st
|
0.84
|
0.46
|
N.st
|
|
4
|
-1.65
|
0.45
|
N.st
|
0.37
|
0.34c
|
N.st
|
|
2
|
-1.93
|
0.31
|
N.st
|
0.21
|
0.46
|
st
|
|
1
|
-1.95
|
0.31
|
N.st
|
0.56
|
0.46
|
N.st
|
|
2
|
-1.77
|
-2.88
|
N. st
|
0.98
|
0.46
|
N.st
|
|
13
|
-0.58
|
-2.88
|
N.st
|
1.22
|
0.46
|
N.st
|
Note : le niveau de significativité est à 5%.
90
Tableau B.3 Tests de racine unitaire et
stationnarité en différence première (fréquence
trimestrielle)
|
Variables
|
Lag
|
Adf-t
|
V.adf
|
résul
|
Kpss-
|
V crit
|
résultat
|
|
4
|
-5.313
|
-2.88
|
stati
|
0.05
|
0.46
|
stati
|
|
5
|
-3.764
|
-2.88
|
Stati
|
0.333
|
0.46
|
stati
|
|
4
|
-2.987a
|
-3.439
|
stat
|
0.278
|
0.46
|
stati
|
|
2
|
-5.01
|
-2.88
|
stati
|
0.142
|
0.46
|
Stati
|
|
13
|
-2.71b
|
-1.94
|
stati
|
0.12
|
0.46
|
Stati
|
|
10
|
-3.127
|
-2.88
|
stati
|
0.06
|
0.46
|
stati
|
|
0
|
-11.74
|
-2.88
|
stati
|
0.09
|
0.46
|
stati
|
|
3
|
-5.20
|
-2.88
|
stati
|
0.04
|
0.46
|
stati
|
Note : les variables sont stationnaires à 5%.
91
10 Les chiffres entre parenthèses sont les
écarts-types estimés. Un, deux et trois astérisques
correspondent respectivement à des seuils de significativité de
1%, 5%, 10%.
Tableau B.4 Estimations MCO des modèles
(fréquence trimestrielle)
|
Modèles Coef10.
|
POTI
|
PPA
|
MF
|
PE
|
|
0.87*
|
0.94*
|
0.88*
|
0.93*
|
|
(0.281)
|
(0.303)
|
(0.292)
|
(0.281)
|
|
-0.142
|
0.11
|
0.03
|
(4.675)
|
|
(0.365)
|
(0.158)
|
(0.073)
|
|
|
|
|
|
(9.091)
|
|
0.0058
|
0.0128
|
0.0028
|
0.0083
|
Légende : significativité à 1% (*); 5%
(**); et 10% (* ** ).
Note : période d'estimation : mars 1976-
décembre 1985. Nombre d'observations : 40
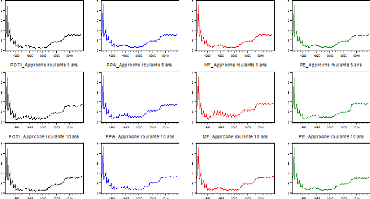
92
Figure B.2 Séries REQM des modèles
et approches(trimestrielles)

93
Figure B.3 Séries U de Theil des
modèles POTI, PPA, MF, PE modifiés par
approche (1986-2014,trimestrielles)
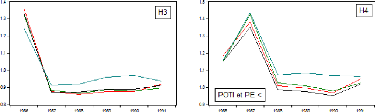
Figure B.4 Séries U de Theil de
l'approche 5 ans par modèle (1986-1991,
trimestrielles)
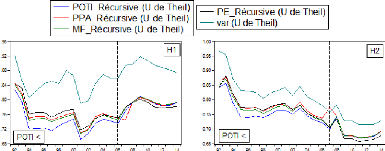
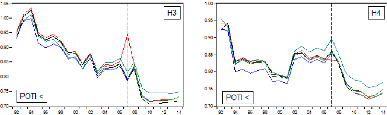
95
Figure B.5 Séries U de Theil de
l'approche récursive par modèle (1992-2014,
trimestrielles)
96
Tableau B.5 Indicateurs IPA et
IPM(fréquence trimestrielle)

*POTI : Parité ouverte de taux de chage/ PPA :
Parité du pouvoir d'achat,/ MF : modèle financier; PE :
modèle avec prix de l'énergie/IPA : Indicateur de Performance par
Approche /IPM : Indicateur de Performance de Modèle
Chinn, M. (2011). Macro Approaches to Foreign Exchange
Determination. La Follette School Working Paper 2011-013.
| 


