Conception d'idéotypes de tomate adaptés au stress hydrique.

2.3 NSGA-II

2.3.1 Notion de domination et le front de Pareto

Sur la Figure2.2, on illustre la notion de domination et le front de Pareto tel que, le point noir :

> domine chacun des carrés.

> est dominé par chacun des triangles.

> n'est pas comparables avec les cercles.

Le front de Pareto représente l'ensemble des points de l'espace de recherche tels qu'il n'existe aucun point qui est strictement meilleur qu'eux (les domine) sur tous les objectifs simultanément. Il s'agit de l'ensemble des meilleurs compromis réalisables entre les objectifs contradictoires, et l'objectif de NSGA-II va être d'identifier cet ensemble de compromis optimaux.

20

FIGURE 2.2 La notion de domination et le front de Pareto.

2.3.2 Historique

NSGA-II (Non-dominated Sorting Genetic Algorithm) a été proposé par [Deb et al, 2002] et est classé comme l'un des algorithmes phares dans le domaine de l'optimisation évolutionnaire multi-objectif. Il tient son appellation de l'algorithme NSGA qui a été proposé auparavant par [Srinvas et Deb, 1994]. L'algorithme NSGA reprend l'idée proposée par Goldberg sur l'utilisation du concept de classement par dominance (sous-section précédente) dans les algorithmes génétiques [Goldberg 1989]. Dans plupart des aspects NSGA-II est très différent de NSGA, cependant le nom a été gardé pour indiquer les origines de cette approche. NSGA-II intègre un opérateur de sélection d'un individu (solution), basé sur un calcul de la distance de "Crowding" (voir sous-section suivante). Comparativement à NSGA, NSGA-II obtient de meilleurs résultats sur toutes les instances présentées dans les travaux de [Deb et al, 2002], ce qui fait que cet algorithme est l'un des algorithmes les plus efficaces pour trouver l'ensemble optimal de Pareto avec une excellente variété des solutions.

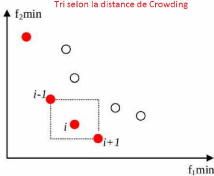
2.3.3 Le principe de la distance de Crowding

La distance de Crowding (ou surpeuplement) est un opérateur de sélection, utilisé pour estimer la densité au voisinage d'un individu (solution) j dans l'espace de recherche. Il calcule la distance moyenne sur chaque objectif, entre les deux points les plus proches situés de part et d'autre de la solution j. Cette distance notée di sert d'estimateur de taille du plus large hypercube incluant le point j sans inclure un autre point de la population et formé par les solutions du même front de Pareto les plus proches de j (voir la Figure2.3, les points rouges appartiennent du même front de Pareto). L'algorithme2 montre les étapes nécessaires pour calculer cette distance (di) pour un individu j.

21

FIGURE 2.3 Le principe de distance de crowding.

Algorithm 2 Calcul de la distance de Crowding d'un individu j sur un front F

1: Initialiser :

l : le nombre d'individus de front F.

di = 0 : pour tout individu j se trouve sur F.

in = 1 : un compteur sur les objectifs.

2: Réordonner l'ensemble F de façon que les valeurs de l'objectif f_m sur ses éléments diminuent. Notons I^m = sort[f_m>](F) le vecteur des indices, c'est à dire I^m_i dénote l'indice de la solution j dans la liste ordonnée selon l'objectif f_m

3: Mettre à jour la valeur de di

Pour chaque solution j telle que 2 I^m_i (l - 1) :

~fm[Im ~

i +1]-fm[Im _i -1]

di = di + max(fm)-min(fm)