Conception d'idéotypes de tomate adaptés au stress hydrique.

2.3.4 Les différentes étapes de NSGA-II

Soient deux populations de même taille N, P(t) (des parents) générée aléatoirement et Q(t) (des enfants) créée à partir de la population P(t), en utilisant les opérateurs génétiques (sélection-croisement-mutation) (voir le projet TER). Ensuite, elles sont réunies en ensemble pour former la population mixte R(t) = P(t) U Q(t), qui est triée selon le principe de dominance en un nombre des fronts de Pareto distincts Rj de la façon suivante : tous les individus non-dominés de R appartiennent à l'ensemble R1 (premier front) ; ensuite, tous les éléments non-dominés de R\R1 sont placés dans l'ensemble R2 (deuxième front) et ainsi de suite jusqu'à ce que tous les individus (solutions) de R(t) soient attribués à un front (voir la Figure2.4, L'algorithme3 montre les étapes nécessaires pour faire un tri de dominance pour une population donnée). Notons que entre deux solutions de même front, aucune ne peut être considérée meilleure que l'autre.

Quand toute la population R(t) est triée, la population suivante P(t + 1) est remplie

22

Algorithm 3 Solution-non-dominées(P) [Deb et al, 2002]

1: for each p E P // P : une population à trier selon le principe de dominance

S_p = O // S_p : une liste ayant contenu tous les individus(solutions) dominés par p

n_p = 0 // n_p : le nombre d'individus(solutions) qui dominent p

for each q E P

if (p -< q) then // si p domine q

S_p = S_p U {q} // mettre q dans S_p

else if (q -< p) then // si q domine p

n_p = n_p + 1

if (n_p = 0) then //p appartient au premier front

pfront = 1

F1 = F1 U {p}

2: i = 1 // Initialize the front counter

while (Fi =6 O)

Q = O // Used to store the members of the next front

for each p E Fi

for each q E S_p

n_q = n_q - 1

if (n_q = 0) then // q appartient au front suivant

qfront = i + 1

Q=QU{q}

i = i + 1

Fi = Q

par les solutions des sous-ensembles non-dominé de R(t) l'un après l'autre en ajoutant les fronts, en commençant par le premier front R1, second front R2, ... etc. Pour choisir les solutions du front qui vont survivre dont seulement une partie peut être placée dans la population suivante, l'opérateur de sélection utilise la distance de Crowding (l'algo-rithme2). Tant que |P(t + 1)| ne dépassent pas N, un tri selon la distance de Crowding est appliqué sur les individus du premier front suivant, non inclus dans P(t+1). Ce tri a pour objectif d'insérer les (N-|P(t+1)|) meilleurs individus (solutions) qui manquent dans la population P(t + 1).

Une fois que les individus appartenant à la population P(t + 1) sont identifiés, une nouvelle population enfant Q(t + 1) est créée. La sélection des individus pour la création de Q(t + 1) à partir de P(t + 1) se fait en utilisant un opérateur sélection appelé de tournoi qui est appliqué entre n individus tirés au hasard dans P(t + 1). Un individu i gagne un tournoi contre un individu j si et seulement si une des deux conditions suivantes est vraie :

> Front(i) < Front(j)

> Ou Front(i) = Front(j) et di > dj

Étant donné que ce tournoi permet à NSGA-II d'éviter le problème de non élitisme, c'est-à-dire perdre le meilleur individu de la population P(t) dans la population P(t + 1).

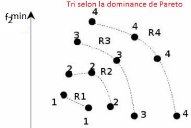
23

FIGURE 2.4 Comparaison basée sur la dominance pour la population R(t).

Le processus continue, d'une génération à la suivante, jusqu'à la dernière. Le scénario général de NSGA-II est illustré dans la Figure2.5 et résumé dans l'algrithme4.

Remarque 2.1. [Deb et al, 2002] ont montré que la complexité du NSGA-II est de l'ordre de O(MN²) où M est le nombre d'objectifs (critères) et N la taille de la population. Cette complexité est induite par la procédure du tri (l'algrithme3) des solutions non dominées de l'algorithme.

Remarque 2.2. NSGA-II a un problème pour résoudre les problèmes ayant un grand nombre des critères, ses performances se détériorent au delà de 3 critères, la plupart des individus (solutions) de la population sont des solutions non dominées, ils ne peuvent pas se déplacer vers la région optimale au sens de Pareto. La taille de la population peut être augmentée pour surmonter ce problème, mais ce qui rend le travail de l'algorithme très lent. Donc une méthode classique "la somme pondérée" a été utilisée pour limiter le nombre de nos critères (les sorties de l'algrithme1) à 2. Elle sera traité dans la section suivante.