2.4 La somme pondérée
Cette méthode de résolution est la plus
évidente et la plus largement utilisée en pratique parmi toutes
les méthodes classiques. Elle consiste à ramener le
problème multi-objectif à un problème d'optimisation
mono-objectif, il s'agit d'associer à chaque fonction objectif un
coefficient de pondération et à faire la somme des fonctions
objectifs pondérées pour obtenir une nouvelle et unique fonction
objectif (l'équatin2.3). Ces coefficients sont
généralement choisis en fonction de l'importance relative que le
décideur attribue à l'objectif.
F = min k i=1 wifi(x), k = 2
(2.3)
Où les poids 0 < wi < 1 sont tels
que k i=1 wi = 1
24
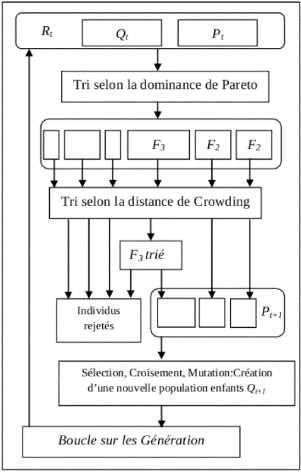
FIGURE 2.5 Le scénario général de
NSGA-II.
25
Algorithm 4 NSGA-II
1: Initialiser les populations P(0), Q(0) de
taille N, L : nombre de génération, t
= 0.
2: while t < L
do
3: R(t) = P(t) ?
Q(t) ;//Création de R(t), P(t) et
Q(t) désignent respectivement la population et la
progéniture à la génération t.
4:
F=Algorithme3(R(t)) //Trier R(t)
selon le principe de dominance, F = (F1, F2, F3, ...).
5: P(t + 1) = Ø, i =
1 ;// La nouvelle population
6: while |P(t + 1)| +
|Fi| < N do
7: P(t + 1) = P(t + 1) ?
Fi ;
8:
Algorithme2(Fi);
9: i + +;
10: end while
11: P(t+1) =
P(t+1)?Fi[1 :
(N-|P(t+1)|)]//Ordonner l'ensemble Fi
selon la distance de Crowding et inclure les N
-|P(t+1)| solutions ayant les valeurs di
les plus grandes.
12: Q(t + 1) =
mak_new_pop(P(t +
1))//Créer la population des enfants Q(t + 1) à
partir de la population des parents P(t + 1).
13: t + +;
14: end while
2.4.1 Utilisation de la somme pondérée
Il est à noter que la variable k (le
nombre des fonctions objectifs dans l'algorithme1) ne prend
que deux valeurs dans ce travail :
> 2 si on fait un ajustement
indépendant (ajuster sous une seule condition (témoin ou stress)
la MFobs et la MSobs d'où deux fonctions objectifs seulement).
> 4 si on fait un ajustement
parallèle (les deux conditions témoin et stress d'où deux
fonctions objectifs par condition). Pour cet ajustement la somme
pondérée est utilisée pour fusionner les 2 fonctions
objectifs par condition à une seule par condition
(l'équation2.4).
fCondition = w ×
fMF + (1 - w) × fMS
(2.4)
Avec w=0.50 : l'importance relative
attribuée aux fonctions objectifs fMF et
fMS est identique, chacune de ces fonction
ayant importance identique.
| 


