Chapitre 2
Méthodologie
Résumé : Nous proposons dans ce chapitre de
présenter les méthodes (algorithmes) principalement
utilisées pour arriver aux objectifs proposés. Dans les deux
premières sections, nous allons montrer comment l'ajustement des
paramètres du modèle peut se transformer en un objectif
d'optimisation mono-objectif et éventuellement multi-objectifs, en
profitant de méthodes (algorithme) existant dans le domaine de
l'optimisation. Et dans les trois sections suivantes, nous présentons un
algorithme évolutionnaire multi-objectif et une méthode classique
choisis pour résoudre notre problème et des critères pour
traiter l'ensemble des solutions trouvées.
2.1 L'optimisation mono-objectif
En optimisation mono-objectif, on cherche à
minimiser/maximiser une fonction objectif unique. Cette fonction objectif varie
en fonction d'un ou plusieurs paramètres chacun de ces paramètres
étant borné (contraintes). On va présenter dans la sous
section suivante comment construire nos fonctions objectifs à partir des
données observées et prédites par le modèle de la
croissance du fruit.
2.1.1 Construction de la fonction objectif
Pour toute condition donnée, le modèle permet la
simulation de la matière fraîche et de la matière
sèche pendant la croissance du fruit à un pas de temps horaire.
Les mesures ont été réalisées au cours du temps.
Comme ces mesures sont destructives, plusieurs fruits ont été
récoltés à des âges après anthèse
variable. En général, le nombre de mesures à la
récolte est très important alors qu'à contrario, peu de
fruit ont été récoltés au cours de la croissance
pouvant aller jusqu'à 1 seule mesure à certaine date. De plus,
les fruits n'ont pas été cueillis toujours au même
âge, mais plutôt sur certaines plages d'âges. Au vu du jeu de
donnée (âge variable, nombre de mesures très variable entre
les différents âges), nous avons, donc construit des clusters
permettant à la fois de regrouper différentes mesures
réalisés dans des fenêtres d'âge proche et permettant
de donner un poids identique à ces différentes dates en prenant
pour chaque cluster la moyenne des différences entre les données
observées et prédites (illustration avec la Figure2.1
: chaque cluster est illustré par une couleur). Dans un
deuxième temps, il a fallu définir une fonction objectif pour
chacune des variables MF et MS. Pour chacune de ces variables, il est
nécessaire de
(2.1)
(2.2)
18
construire une fonction objectif qui nous permettra
d'optimiser la valeur des paramètres. L'objectif de cette fonction doit
être de nous permettre de minimiser les écarts entre les
données simulées et les données observées.
|
nClusterP Pn
1 1
RMSE = (Dobsi,j -
Dpredi,j)2
nCluster n
i=1 j=1
|
Les variables de l'équation
(équatin2.1) sont :
Dobs : (MF ou MS).
Dpred :(MFpred ou MSpred).
nCluster : nombre de culster.
n : nombre de points des données
observées au niveau de culster i.
La fonction à minimiser est le RRMSE
(équatin2.2), aussi bien pour la matière
fraîche que pour la matière sèche. L'objectif est bien de
trouver la meilleure combinaison de paramètre permettant de simuler le
mieux possible la matière fraîche et la matière
sèche, donc de minimiser simultanément RRMSEMF et RRMSEMS. Nous
nous trouvons donc dans la situation d'avoir à optimiser sur deux
critères, et nous nous plaçons dans le cadre
général de l'optimisation multi-objectifs (voir section
suivante).
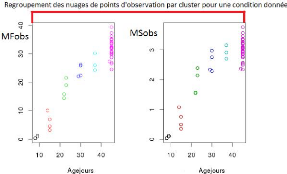
FIGURE 2.1 Le principe de regroupement par cluster.
| 


