ANNEXES
A1- Technique
d'interpolation des séries de Goldstein et Khan
Cette technique consiste à transformer ou
ramener des séries économiques dont les valeurs sont cumulatives
pour une année, en séries trimestrielles. En d'autres termes,
cela consiste à ramener les données d'une variable
économique établie annuellement, en données
trimestrielles. Ce le cas de variables telles que le revenu, les
dépenses, etc.
NB : Ce ne
sont pas toutes les variables économiques qui suivent untel processus
d'interpolation.
Supposons une variable Y
dont les observations sont annuelles, et nous voulons générer des
observations trimestrielles. L'objectif est d'approximer le graphique de   par rapport aux points où les valeurs de
Y sont connues. par rapport aux points où les valeurs de
Y sont connues.
Si on représente f (x) par une
fonction de second degré donnée par :
  [20] [20]
Alors, pour trois (3) observations annuelles
consécutives (périodes 0, 1 et 2) de Y,
l'approximation du graphique de Y prendra la
forme :



La résolution de ces trois (3)
intégrales donne les équations suivantes :



Par contre, les graphiques trimestrielles sont
approximés en divisant une année par quatre (4) trimestres de
0.25 de distance chacune. Ce qui donne :
Premier trimestre (T1) :  
Deuxième trimestre (T2) :  
Troisième trimestre (T3) :  
Quatrième trimestre (T4) :  
Les résultats des intégrations
donnent :




Ce sont ces équations qui serviront à
générer les valeurs des observations trimestrielles. Il est
à noter que pour chaque trimestre, la pondération de la
période courante (t) est plus importante que
celle de la période antérieure (t-1) ou postérieure
(t+1). Pour les deux (2) premiers trimestres,
l'année t-1 ont des pondérations
beaucoup plus meilleures que celles de l'année
t+1. De plus, la somme des pondérations de
chaque trimestre doit être égale à 0.25 afin que les
graphiques trimestrielles puissent correspondre à ceux annuels.
A2- Formulation des relations de Hicks -
Shephard
L'approche traditionnelle et conventionnelle utilisée
pour mesurer l'impact des changements de prix sur le bien - être ou la
consommation des ménages, repose sur l'analyse d'effet de la variation
des prix sur le surplus du consommateur et/ou du surplus du producteur. Et du
fait de la nature ambigüe de certains ménages (à la fois
producteurs et consommateurs), un autre conceptfut développé, le
modèle de la variation compensatoire de Hicks donné par :
  [25] [25]
OùE désigne les
dépenses minimums permettant au ménage
h d'atteindre un certain niveau d'utilité
u, p le vecteur des prix,
0 et 1 désignant
respectivement les situations avant et après les changements de prix.
Mais la nature infinitésimale des variations de prix,
permet d'ajuster la relation [25] et d'avoir celle de Shephard :
 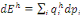 [26] [26]
Où qi
désigne la quantité du bien i
consommée par le ménage h.
Ainsi, la relation [26] permet donc de réécrire
la relation [24] sous cette forme :
  [27] [27]
A3- Stationnarité des séries
Tableau 6 :
Résultats des tests de stationnarité à
niveau de Dickey - Fuller Augmenté
|
Modèle
|
T_stat
|
Valeurs critiques
|
Décision sur H0
|
|
1%
|
5%
|
10%
|
|
TCDCM
|
1
|
-7.304522
|
-2.616203
|
-1.94814
|
-1.61232
|
Rejetée*
|
|
2
|
-7.25581
|
-3.581152
|
-2.926622
|
-2.601424
|
Acceptée
|
|
3
|
-7.169913
|
-4.170583
|
-3.51074
|
-3.185512
|
Acceptée
|
|
TCIPA
|
1
|
-7.154546
|
-2.617364
|
-1.948313
|
-1.612229
|
Rejetée*
|
|
2
|
-7.235318
|
-3.584743
|
-2.928142
|
-2.602225
|
Acceptée
|
|
3
|
-7.148568
|
-4.17564
|
-3.513075
|
-3.186854
|
Acceptée
|
|
TCPR
|
1
|
-2.82436
|
-2.619851
|
-1.948668
|
-1.612036
|
Rejetée*
|
|
2
|
-3.179607
|
-3.592462
|
-2.931404
|
-2.603944
|
Acceptée
|
|
3
|
-3292205
|
-4.186481
|
-3.51809
|
-3.189732
|
Acceptée
|
|
TCMA
|
1
|
-4.176120
|
-2.615093
|
-1.947975
|
-1.612408
|
Rejetée*
|
|
2
|
-4.283207
|
-3.577723
|
-2.925169
|
-2.600658
|
Acceptée
|
|
3
|
-4.20027
|
-4.165756
|
-3.508508
|
-3.184230
|
Acceptée
|
|
TCPLU
|
1
|
-1.615536
|
-2.619836
|
-1.948686
|
-1.612036
|
Rejetée**
|
|
2
|
-2.173347
|
-3.592462
|
-2.931404
|
-2.603944
|
Acceptée
|
|
3
|
-2.597635
|
-4.186481
|
-3.518090
|
-3.189732
|
Acceptée
|
|
1
|
-2.349742
|
-2.621185
|
-1.948886
|
-1.611932
|
Rejetée
|
|
2
|
-3.458483
|
-3.596616
|
-2.933158
|
-2.604867
|
Rejetée
|
|
TCPA
|
3
|
-3.457915
|
-4.192337
|
-3.520787
|
-3.191277
|
Acceptée
|
H0 : Présence de racine unitaire ou série
non stationnaire
*significatif à 5%
**significatif à 10%
(1) Modèle sans constante ni tendance ;
(2) Modèle avec constante ;
(3) Modèle avec constante et tendance.
A4- Estimations et tests de diagnostic
Tableau 7 :
Résultats d'estimations
|
|
TCPR
|
TCMA
|
TCPLU
|
TCPA
|
R²
|
R² ajusté
|
|
TCIPA
|
Coefficient
|
-0.1459
|
0.0118
|
0.0070
|
-0.0909
|
0.1996
|
0.1437
|
|
Ecart-type
|
0.0860
|
0.0266
|
0.0027
|
0.0875
|
|
t-Stat
|
-1.6968
|
0.4426
|
2.6160
|
-1.0387
|
|
TCDCM
|
Coefficient
|
0.7742
|
-.01605
|
-0.00156
|
0.1304
|
0.3779
|
0.3345
|
|
Ecart-type
|
0.1724
|
0.0534
|
0.0054
|
0.1766
|
|
t-Stat
|
4.4892
|
-3.0039
|
-0.2886
|
0.7381
|
Tableau
8 : Corrélogramme des résidus de
l'estimation de l'équation [18]
|
Date: 07/21/12 Time: 07:12
|
|
|
|
|
Sample: 2000Q1 2011Q3
|
|
|
|
|
|
Included observations: 47
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Autocorrelation
|
Partial Correlation
|
|
AC
|
PAC
|
Q-Stat
|
Prob
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
**| . |
|
**| . |
|
1
|
-0.205
|
-0.205
|
2.1065
|
0.147
|
|
.*| . |
|
**| . |
|
2
|
-0.187
|
-0.239
|
3.9018
|
0.142
|
|
. | . |
|
.*| . |
|
3
|
-0.056
|
-0.169
|
4.0639
|
0.255
|
|
. |** |
|
. |*. |
|
4
|
0.235
|
0.150
|
7.0343
|
0.134
|
|
. |*. |
|
. |*. |
|
5
|
0.080
|
0.161
|
7.3871
|
0.193
|
|
**| . |
|
**| . |
|
6
|
-0.312
|
-0.207
|
12.871
|
0.045
|
|
.*| . |
|
.*| . |
|
7
|
-0.079
|
-0.171
|
13.226
|
0.067
|
|
. |*. |
|
. | . |
|
8
|
0.170
|
-0.008
|
14.935
|
0.060
|
|
. |*. |
|
. |*. |
|
9
|
0.185
|
0.159
|
17.014
|
0.048
|
|
**| . |
|
.*| . |
|
10
|
-0.308
|
-0.147
|
22.930
|
0.011
|
|
.*| . |
|
.*| . |
|
11
|
-0.126
|
-0.142
|
23.939
|
0.013
|
|
. |** |
|
. |*. |
|
12
|
0.293
|
0.146
|
29.591
|
0.003
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau
9 : Corrélogramme des résidus de l'estimation de
l'équation [17]
|
Date: 07/21/12 Time: 07:14
|
|
|
|
|
Sample: 2000Q1 2011Q3
|
|
|
|
|
|
Included observations: 47
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Autocorrelation
|
Partial Correlation
|
|
AC
|
PAC
|
Q-Stat
|
Prob
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.*| . |
|
.*| . |
|
1
|
-0.091
|
-0.091
|
0.4176
|
0.518
|
|
. | . |
|
. | . |
|
2
|
-0.047
|
-0.056
|
0.5303
|
0.767
|
|
. |*. |
|
. |*. |
|
3
|
0.120
|
0.112
|
1.2826
|
0.733
|
|
.*| . |
|
.*| . |
|
4
|
-0.155
|
-0.139
|
2.5684
|
0.632
|
|
. | . |
|
. | . |
|
5
|
0.072
|
0.061
|
2.8497
|
0.723
|
|
. | . |
|
. | . |
|
6
|
0.007
|
-0.010
|
2.8527
|
0.827
|
|
. | . |
|
. | . |
|
7
|
0.026
|
0.068
|
2.8911
|
0.895
|
|
**| . |
|
**| . |
|
8
|
-0.224
|
-0.267
|
5.8538
|
0.664
|
|
.*| . |
|
.*| . |
|
9
|
-0.074
|
-0.086
|
6.1897
|
0.721
|
|
. | . |
|
.*| . |
|
10
|
-0.040
|
-0.108
|
6.2913
|
0.790
|
|
.*| . |
|
.*| . |
|
11
|
-0.144
|
-0.104
|
7.6139
|
0.747
|
|
. | . |
|
.*| . |
|
12
|
0.031
|
-0.075
|
7.6775
|
0.810
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 10 :
Tests résiduels
d'hétéroscédasticité, d'auto corrélation et
de normalité
|
Tests
|
Statistique
|
Valeur
|
Probabilité
|
|
Hétéroscédasticité
|
TCIPA
|
F
|
0.492831
|
0.614226
|
|
TCDCM
|
F
|
|
|
|
Auto corrélation
|
TCIPA
|
DW
|
1.733018
|
0.003306
|
|
TCDCM
|
DW
|
2.003499
|
0.806563
|
|
Normalité
|
TCIPA
|
J - B
|
3.486063
|
0.174989
|
|
TCDCM
|
J - B
|
536.7580
|
0.00000
|
(1) H0 : Homoscédastique
(2) H0 : Absence d'autocorrélation d'ordre h
(3) H0 : Normalité
Source : Les estimations de l'auteur sur
Eviews
| 


