Conclusion
Nous avons dans ce chapitre donné une
présentation générale de la programmation
mathématique à deux niveaux et présenté quelques
algorithmes de résolution dans le cas de l'unicité de la solution
du suiveur. Mais il se trouve que dans la plupart des cas, les problèmes
modélisés sous formes de PBN sont tels que le problème du
second plan admet plus d'une solution ; ce qui complique
considérablement le problème. Dans le chapitre suivant, nous
allons présenter les différentes techniques
développées pour attaquer les PBN dans ce cas ; ce qui nous
permettra par la même occasion de définir la notion de
problèmes d'optimisation mal posés.
CHAPITRE DEUX
Non unicité de la solution du problème
du
suiveur : les différentes techniques
d'approches.
Mémoire de DEA * Laboratoire
d'analyse numérique * UYI Francisque.D.Fouodji
c~UYI 2007-2008
Dans toute la suite, lorsque nous dirons "cas de la non
unicité", ce sera pour dire "cas de la non unicité de la solution
du problème du suiveur".
Introduction
Au chapitre un, nous avons présenté quelques
résultats d'optimalité et quelques algorithmes de
résolution des PBN dans le cas de l'unicité de la solution du
suiveur. Il se trouve cependant que dans la plupart des applications, le
problème du suiveur n'admet pas une solution unique; d'où la
nécessité d'explorer de nouvelles techniques afin de
résoudre les PBN dans ce cas plus général.
Les PBN dans le cas de la non unicité font partie d'une
classe plus large de problèmes de programmation mathématique :
les problèmes de programmation mathématique
mal-posés.
Définition 2.0.1. Soit E un
espace de Banach reexif, ó une topologie sur E, K
un convexe fermé non vide de E et h :
K -* R U {+oo}
Le problème de programmation mathématique :
est dit bien-posé au sens de TIKHONOV (resp
bien-posé au sens général) suivant la topologie
ó, s'il existe une solution unique u0 à (2.1)
et toute suite minimisante 1 de (2.1)
ó-converge vers u0 (resp (2.1) a au plus une solution
et toute suite minimisante admet une sous suite qui ó-converge
vers la solution unique.)
Un problème de programmation mathématique est dit
mal-posé s'il n'est pas bien-posé.
Commençons par présenter la position du
problème dans la resolution des PBN dans le cas de la non
unicité.
|
1Une suite
(un)n ? K
est appelé suite minimisante si uim
n?+8
|
h(un)
= inf
h(v).
v?K
|
Par définition de l'infimum, une telle suite existe
toujours.
Non unicité de la solution du problème
du suiveur : les différentes techniques d'approches. 21
2.1 Position du problème
Considérons une nouvelle fois le PBN :
|
«min
y
|
{ }
» F(x, y) : G(y) <
0, x E Ø(y) (2.2)
|
|
Où
|
Ø(y) = Argmin
x
|
{ }
f(x, y) : g(x, y) <
0, h(x, y) = 0 (2.3)
|
Pour y fixé, Ø(y) est l'ensemble
des solutions du problème.
{ }
min f(x, y) : g(x, y) <
0, h(x, y) = 0 (2.4)
x
F : Rn X Rm -? R, f :
Rn X Rm -? R, G : Rn X Rm
-? Rp,
g : Rn X Rm -? Rq sont des
fonctions suffisamment2 régulières.
{ }
Posons Y = y E Rm :
G(y) < 0 et supposons que Y est fermé.
Les guillemets dans (2.2) expriment l'incertitude de la
définition de (2.2) dans le cas de la non unicité; car lorsque
Ø(y) n'est pas réduit à un singleton pour tout
y E Rm, le leader se trouve face à un dilemme.
En effet, pour prendre sa décision (qu'il souhaite
optimale), le leader doit savoir qu'elle sera la décision du suiveur.
Dans le cas où il existe plusieurs décisions possibles pour le
suiveur, le leader se trouve dans l'embarras (car il ne sait sur laquelle
portera le choix de celui-ci).
La question qu'on se pose ici est celle de savoir : comment
aborder le PBN (2.2)-(2.3) dans le cas de la non unicité de la solution
de (2.4) ?
L'exemple suivant illustre les difficultés qu'on peut
rencontrer dans le cas de la non unicité.
Exemple 2.1.1. On considère le PBN :
|
«min
y
|
{ }
» x2 + y2 : x
E Ø(y), -1 < y < 1
|
|
Où Ø(y) = Argmin
x
On a :
|
{-xy : 0 < x < 1}
|
|
Ø(y) :=
|
{
|
{0} si y < 0
{1} si y >
0
[0,1] si y = 0
|
Ainsi,
|
F(x(y), y) =
|
{
|
y2 si y < 0
1 + y2 si y > 0 E [0,1]
si y = 0
|
. (2.5)
|
Mémoire de DEA * Laboratoire d'analyse
numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008
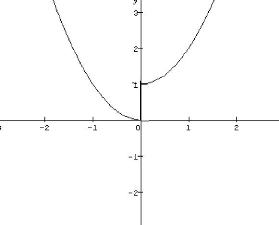
Le tracé de F est le suivant :
2Suivant les résultats que nous
énoncerons, nous exigerons que ces fonctions satisfassent des
propriétés de régularité parfois
différentes
Non unicité de la solution du problème du
suiveur : les différentes techniques d'approches.
22
Mémoire de DEA *
Laboratoire d'analyse numérique *
UYI Francisque.D.Fouodji c~UYI 2007-2008
FIG. 2.1 Sur les difficultés rencontrées dans le
cas de la non unicité
pour y = 0; on a W(y) = [0,
1]. Donc pour ce paramètre, W(y) contient une
infinité d'éléments. On se trouve donc ici dans le cas de
la non unicité.
d'après (2.5), l'expression de la fonction objectif
n'est connue que si le suiveur annonce clairement son choix; la
solvabilité du problème du leader dépend de ce choix. En
effet, si le suiveur fait le choix x(0) = 0 E W(0) alors le
problème du leader est solvable; la solution optimale du PBN est
(0, 0) et la valeur de la fonction objectif du leader est
0.
{ F (x(y), y) = y2
: -1 y < 0 }
min
y
le PBN n'admet pas de solution dans ce cas car
F(x(y), y) = y2 est
dérivable et on a
Si le choix du suiveur se porte sur x(y) = 0
E W(y), avec y < 0 alors le problème du leader
devient :
VF(x(y),y) =
(0,2y)
VF(x(y),y) = 0 =' y
= 0
Or y = 0 ne satisfait pas à la contrainte
-1 y < 0 donc le problème du leader n'admet pas de
point critique et par conséquent n'admet pas de solution.
Jusqu'ici, trois approches ont été
développées dans la littérature pour résoudre les
PBN dans le cas de la non unicité : l'approche optimiste, l'approche
péssimiste et l'approche par régularisation sur laquelle porte
notre travail.
| 


