Dans le chapitre 2, nous avons proposé une nouvelle
technique de réduction du niveau de PAPR. Nous avons expliqué les
bases et les fondaments de la nouvelle forme d'onde, nous avons apporté
des justifications théoriques de la viabilité de la nouvelle
forme d'onde qui est sensée avoir un PAPR très faible.
Le présent chapitre sera consacré à
l'étude des performances de cette nouvelle forme d'onde. Les
performances de cette solution seront évaluées analytiquement et
par simulations.
· Dans une première section, nous
présenterons les performances de cette forme d'onde selon plusieurs
critères notamment le gain en réduction du PAPR,l'ACPR.
· Ensuite, nous étudierons la mise en oeuvre de
la nouvelle forme d'onde au niveau de l'émetteur et au niveau du
récepteur c.à.d proposer un critère adéquat et
fiable pour la décision. Nous donnerons à la fin de cette partie
un schéma d'optimisation de la nouvelle forme d'onde.
3.1 Performances de la nouvelle forme d'onde
Dans la présente section, nous avons simulé un
certain nombre de critères, de paramètres qui permettent
d'évaluer ou de comparer les techniques de réduction du PAPR.
Les
- 39 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
simulations réalisées ont été
faites pour un système OFDM avec 64 sous-porteuses et modulées
avec des symboles BPSK selon le mapping suivant:
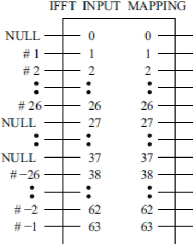
Figure 3.1: Mapping des sous-porteuses à
l'entrée de l'IFFT
la Figure 3.1, correspond au mapping de la couche physique de
la norme 802.11, couramment appélée "Wifi" [1], le tableau 3.1
résume les paramètres de simulation utilisés pour les
différentes simulations.
Tableau 3.1: Paramètres de simulation
Type de Modulation BPSK / Duobinaire
Nombre de sous-porteuses 64
sous-porteuses de données 58
Nombre de pilots 4
Facteur de sur-échantillonnage 1 4
Type de canal AWGN
- 40 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
3.1.1 Taux d'erreur binaire
Pour certaines techniques, la réduction du PAPR peut
s'accompagner de la génération de distorsions aussi bien à
l'extérieur qu'à l'intérieur de la bande utile du signal;
c'est le cas par exemple des techniques de clipping. Dans le chapitre
II, nous avons modéliser le clipping par une transformation
polynomiale ce qui met en évidence les termes d'intermodulation et les
harmoniques générés.
Comme la détection des symboles OFDM se fait dans le
domaine fréquentiel, il vient alors que ces distorsions en particulier
celles qui sont à l'intérieur de la bande utile du signal vont
dégrader le TEB s'il s'agit d'une technique de clipping and
filtering simple. Par contre le clipping effectué dans la nouvelle
technique de réduction du PAPR n'entraine pas de dégradation du
TEB. La Figure 3.2 illustre la disposition du spectre "instantanné" du
système OFDM après le codage duobinaire, c'est-à-dire
après le gain spectral du codage duobinaire.
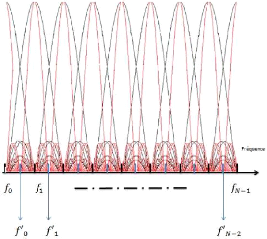
Figure 3.2: Gain de spectre dans chaque
sous-porteuse
On obtient un jeu de sous-porteuses (en rouge sur le
schéma) qui ne se chevauchent pas comme pour le schéma classique
de l'OFDM . En effet il existe des sous-porteuses "virtuelles", qui
correspondent à des trous spectraux, aux fréquences J
' 0, J '
1,..., J '
N-1 comme le montre la Figure 3.2. C'est sur
ces fréquences que se fera l'ajout du signal de clipping. Ceci
constitue un résultat assez important; d'après nos connaissances
il s'agit là d'une nouvelle et attrayante contribution.
- 41 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
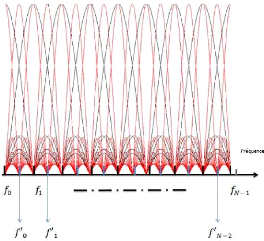
Figure 3.3: Sous-porteuses additionnelles pour le signal de
réduction du PAPR
Le système illustré dans la Figure 3.3
correspond au spectre réduit de l'OFDM duobinaire avec l'ajout de
nouvelles sous-porteuses orthogonales à celles de l'OFDM duobinaire.
On obtient l'équivalent de l'OFDM traditionnel mais
avec une fenêtre temporelle deux fois plus grande et donc un espacement
fréquentiel entre les sous-porteuses plus réduit. Les
sous-porteuses J i
'utilisées par le signal de réduction du PAPR
et les sous-porteuses Ji initialement utilisées pour
générer les symboles OFDM sont orthogonales. C'est cette
orthogonalité qui assure un décodage des symboles à la
réception. Nous détaillerons dans la Section 3.2.1, le processus
de décodage de la nouvelle forme d'onde à la réception.
3.1.2 Performances en termes de réduction du
PAPR
Ce critère est immédiat et constitue le
critère de mérite essentiel des techniques de réduction du
PAPR. Pour deux techniques de réduction du PAPR X et Y
, avec des signaux de sorties respectifs x(t) et y(t),
les PAPR de x(t) et y(t) sont définis comme
Chapitre 3 : Performances de la Nouvelle forme d'onde
suit:
max
|xn|2
PAPR[x](ö) = Pr[
0=n=Ts
Px = ö]
PAPR[y](ö) = Pr[
(III.1)
max
|yn|2
0=n=Ts
Py = ö]
- 42 -
où Ts désigne la
durée d'un symbole OFDM et Px et
Py représentent respectivement les puissances
moyennes des signaux x(t) et y(t). Le PAPR
est une variable aléatoire qui peut être
caractérisée par sa CCDF définie par:
CCDF(PAPR0) = Pr(PAPR
= PAPR0) (III.2)
Les PAPR[x] et
PAPR[y] définis par l'équation III.1, sont
des variables aléatoires dont les CCDFs sont représentés
sur la Figure 3.4. Pour un niveau de CCDF donné, CCDF = ö,
on défini le gain en réduction de PAPR
ÄPAPR(ö) par:
ÄPAPR(ö) =
PAPR[x](ö)-PAPR[y](ö),[dB]
(III.3)
où PAPR[x]
et PAPR[y] sont les valeurs du PAPR des
signaux x(t) et y(t) à CCDF
= ö.

Figure 3.4: Calcul du gain en réduction du PAPR
à une valeur particulière de la CCDF
C'est sur la base de la CCDF que se fera les mesures de
performances en terme de gain en PAPR.
- 43 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
Courbes générales du PAPR
Dans la littérature et comme abordé dans le
chapitre 1, plusieurs formules permettent d'approximer le PAPR des signaux
OFDM. Aussi il convient d'étudier ces différentes approximations
par rapport à la distribution de l'OFDM BPSK simulé selon les
paramètres du tableau 3.1.
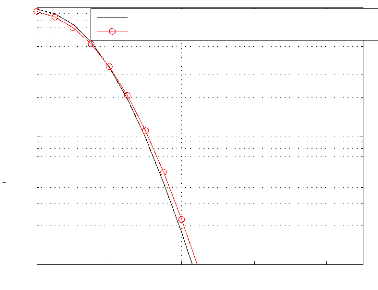
100
OFDM discret (Facteur sur-échantillonnag=1)
simulée Approximation théorique de Van Nee
10-1
10-2
CCDF = Pr(PAPR>ë)
5 7 9 11 13
ë (in dB)
Figure 3.5: Distribution du PAPR théorique et
simulé dans le cas d'une constellation BPSK
- 44 -
Chapitre 3 : Performances de la Nouvelle forme d'onde

100
10-2
OFDM continu ( facteur surechant=4) Approximation de Van Nee
Approx de Ochai et Imai Approx de Y. Louet et H. Sajjad Approx de Zhou et
Caffery
10-10
5 6 7 8 9 10 11 12 13 14
ë (in dB)
CCDF = Pr(PAPR>ë)
10-4
10-6
10-8
Figure 3.6: Distribution du PAPR théorique et
simulé pour l'OFDM continu dans le cas d'une constellation BPSK
La comparaison entre les courbes théoriques et
simulées est faite sur les Figures 3.5 pour le PAPR du signal OFDM
discret, et 3.6 pour le PAPR du signal OFDM continu. Les courbes
théoriques et simulées sont très proches, ce qui nous
indique la haute précision et la fiabilité des différentes
approximations du PAPR rencontrées dans la littérature.
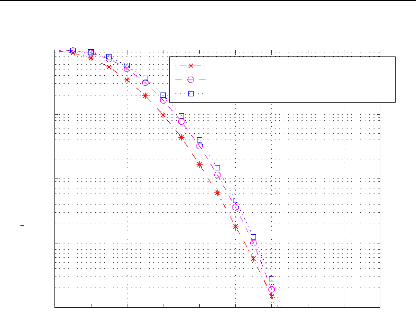
La Figure 3.7 présente la CCDF du signal OFDM pour
N = 64 et pour différentes valeurs du facteur de
sur-échantillonnage.
- 45 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
CCDF = Pr(PAPR>ë)
10-2
100
OFDM avec facteur surechantillonnage=1 OFDM avec facteur
surechantillonnage=2 OFDM avec facteur suréchantillonnage=4
10-1
10-3
10-4
5 6 7 8 9 10 11 12 13 14
ë (in dB)
Figure 3.7: Effet du suréchantillonnage sur le
PAPR
Nous remarquons, d'après la Figure 3.7, que plus le
facteur de sur-échantillonnage est élévé, plus l'on
approche le comportement d'un signal OFDM continu. Les plus grandes variations
de la CCDF se produisent quand le facteur de sur-échantillonnage passe
de L = 1 à L = 2; on n'a pas une variation
significative de la CCDF pour L > 4.
Interprétation: En augmentant le facteur de
sur-échantillonnage, on augmente la précision
d'échantillonnage du signal OFDM, ce qui permet de gagner en
précision sur les valeurs du signal OFDM continu. Ainsi, on calcule
mieux les valeurs crêtes du signal OFDM et cela influe sur le PAPR.
Cependant pour L > 4, il n'y a plus d'augmentation significative de
la CCDF, c'est pourquoi on se limitera à un facteur de
sur-échantillonnage de 4 pour calculer le PAPR du signal OFDM
continu.
La nouvelle forme d'onde étant essentiellement
basée sur le codage duobinaire, il nous faut vérifier avant tout
que le codage duobinaire en lui même n'augmente pas le PAPR. Dans la
Figure 3.8 nous effectuons la comparaison entre la courbe de la CCDF otenue
pour des systèmes OFDM modulés avec du BPSK et celle obtenue par
le codage duobi-naire sur chacune des sous-porteuses. Comme on peut le
constater, les deux courbes
- 46 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
sont très proches. Ceci revient à dire que
même après le gain de spectre, on obtient les mêmes
performances en terme de CCDF, d'où la pertinance d'un tel
résultat!
1 3 5 7 9 11
ö

CCDF=Pr(PAPR>= ö)
100
10-1
10-2
10-3
10-4
OFDM BPSK OFDM Duobinaire
Figure 3.8: Le codage duobinaire n'augmente pas le
PAPR.
Gain de PAPR de la nouvelle forme d'onde
Dans cette section, nous mettons en oeuvre la nouvelle forme
d'onde et nous étudions la dimunition du PAPR obtenue. Dans une
première partie nous décrirons l'algorithme d'ajout du signal
après codage duobinaire; puis nous présenterons les gains de PAPR
obtenus.
L'algorithme d'ajout de signal se fait de la façon
suivante: Étape 1 :
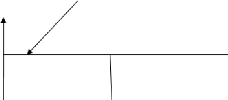
· Considérer les symboles OFDM duobinaires
temporels par paire, parce que chaque symbole OFDM s'étale à
présent sur 2T temporels, comme on peut le voir sur la Figure
3.9, T étant la durée symbole OFDM d'origine.
Chapitre 3 : Performances de la Nouvelle forme d'onde

- 47 -
Figure 3.9: Etalement temporel des symboles OFDM
Étape 2:
· Generer ici le signal d'"ajout" :
c(t) = -(s(t) -sclip(t))
(III.4)
où s(t) est le signal OFDM duobinaire, et
sclip(t) est le signal OFDM duobinaire écrêté
à un seuil Clipseuil.
On effectue un filtrage (FFT/IFFT) du signal c(t) qui
consiste à faire une FFT de taille 2N sur le signal de clipping
et à filtrer les composantes fréquentielles OOB,
et celles correspondant aux fréquences f =
f0, f = f0 + 1 T ,. . . ,f = f0 +
N-1
T car
ces fréquences sont utilisées pour l'envoi des
données. Étape 3
· Générer à nouveau le signal
d'ajoutfiltré dans le domaine temporel, on notera ce
signal par c1(t). Étape 4
· Le signalfinal qui correspond à la nouvelle
forme d'onde s'écrit: às(t) = c1(t) +
s(t).
Chapitre 3 : Performances de la Nouvelle forme d'onde
Pour les simulations, nous testons les performances de notre
algorithme pour plusieurs valeurs de seuil de clipping et nous
aboutissons aux constatations suivantes.
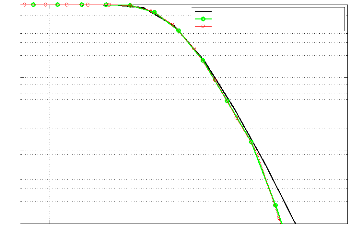
Dans la Figure 3.10, où nous comparons le PAPR de la
forme d'onde avec le PAPR de la technique de clipping andfiltering
pour un seuil de clipping de 10dB
CCDF( ö )= Pr(PAPR >= ö)
100
10-1
10-2
10-3
2 3 4 5 6 7 8 9 10 11 12 13
OFDM
Nouvelle forme d'onde avec taux de clipping ñ=10 dB
clipping and filtering avec taux de clipping ñ=10 dB
- 48 -
ö
Figure 3.10: PAPR pour un clipping à 10 dB
On constate qu'on n'a pratiquement pas de dimution du PAPR, en
effet pour de grandes valeurs du "seuil d'écrêtage", les
crêtes du signal en entrée du clipping n'atteignent plus le "seuil
d'écrêtage"; dans ce cas il n'y a plus d'écrêtage (et
donc il n'y a pas de réduction de PAPR). Le signal à la sortie de
"clipping" est égal au signal à l'entrée.
- 49 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
2 3 4 5 6 7 8 9 10 11 12 13
ö

CCDF(ö)=Pr(PAPR >= ö)
100
10-1
10-2
10-3
OFDM
Nouvelle forme d'onde avec le taux de clipping ñ=2
clipping and filtering avec taux de clipping ñ=2
Figure 3.11: PAPR pour un clipping à 2 dB
La Figure 3.11 illustre la comparaison entre la technique
de clipping filtering traditionnelle pour un seuil de 2 dB
avec la mise en oeuvre de la nouvelle forme d'onde pour le même
seuil. On remarque une dimunition du PAPR de la nouvelle forme d'onde, mais ce
gain de PAPR n'atteint pas celui de la technique traditionnelle de
clipping car la nouvelle forme d'onde n'utilise pas toutes les
fréquences pour générer le signal de clipping.
Pour cette technique, plus le niveau de clipping est
élévé, plus grand sera la dimution du PAPR. Les signaux
additionnelle de clipping et les signaux OFDM duobinaires sont orthogonaux donc
n'interfèrent pas, il est donc possible de faire un
écrètage plus rude (avec un seuil très bas ou avec
d'autres techniques de clipping comme le deep clipping).
- 50 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
2 3 4 5 6 7 8 9 10 11 12 13
ö
CCDF(ö)=Pr(PAPR >= ö)
100
10-1
10-2
10-3
OFDM
nouvelle forme d'onde avec clipping au taux ñ=2dB
nouvelle forme d'onde avec clipping au taux ñ=10dB nouvelle forme d'onde
avec clipping au taux ñ=10dB
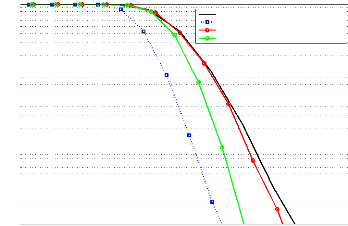
Figure 3.12: Gain de PAPR de la nouvelle forme pour
plusieurs taux de clipping.
La Figure 3.12 illustre le gain de PAPR de la nouvelle forme
d'onde pour plusieurs valeurs du taux de clipping qui varient de 0 à 10.
Plus le seuil de clipping augmente, plus le PAPR dimunie et tant que le signal
de clipping n'impacte pas les performances en terme de TEB ou d'ACPR de la
nouvelle forme d'onde on pourrait effectuer le clipping selon n'importe quel
seuil.
Le PAPR devient "paramétrable" en changeant le taux de
clipping : c'est dire toute l'efficacité de cette nouvelle forme d'onde,
car dépendamment de la norme et pour des applications qui exigent un
niveau de PAPR tres faible, notre technique permet d'avoir un gain
considérable comparé à l'OFDM classique en
paramétrant le seuil de clipping.
3.1.3 Dimunition de l'ACPR
L'Adjacent Channel Power Ratio (ACPR) mesure le rapport entre
le niveau de puissance dans la bande de fréquence utile par rapport
à celui dans la bande adjacente, on parle d'ACPR droite et d'ACPR gauche
suivant le côté de la bande adjacente prise en compte. L'ACPR est
donnée par la relation III.5:
f
BdeUtile DSP( f )d f
ACPR =
R
(III.5)
BdeAdjacente DSP( f )d f
- 51 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
L'ACPR est déterminant dans l'implémentation de
n'importe quelle norme radio mobile. En effet les organismes de
régulation du spectre imposent un masque pour les spectres des
différents réseaux radio-mobile, enfin de répartir au
mieux l'espace de spectre entre les différents usages.
Certaines techniques de réduction du PAPR peuvent
entrainer une augmentation de l'ACPR, par exemple le clipping engendre
une rémontée des lobes secondaires et donc une augmentation de
l'ACPR.
Dans la mise en oeuvre de la nouvelle forme d'onde, nous
effectuons un filtrage OOB du signal de clipping, c'est-à-dire
une élimination du signal qui se trouve dans le spectre adjacent au
spectre utile. Ainsi, une possible augmentation de l'ACPR ne peut provenir que
du codage duobinaire. Le codage duobinaire tel qu'il est effectué dans
l'OFDM n'augmente pas l'ACPR. Les simulations des spectres de l'OFDM duobinaire
présentées dans le chapitre 2 dans la partie 2.2, montrent une
dimunition du niveau des lobes secondaires des sinc(sinus cardinal) qui forment
le spectre du signal OFDM duobinaire; ce qui implique une dimunition du niveau
des composantes OOB et donc de l'ACPR. Tous ces éléments, nous
permettent de conclure que la nouvelle forme d'onde permet d'avoir un ACPR plus
faible que celui d'un système OFDM classique.
3.1.4 Variation de la puissance moyenne
Pour certaines techniques, la réduction du PAPR
s'accompagne d'une diminution ou d'une augmentation de la puissance moyenne du
signal à transmettre. Par exemple, dans le cas de l'utilisation de la
technique de clipping, la puissance moyenne du signal à
transmettre est réduite tandis que dans un contexte de Tone
Reservation, la puissance moyenne du signal à transmettre est
augmentée parce qu'on ajoute du signal additionnel dans les
sous-porteuses libres. La variation de la puissance moyenne du signal à
transmettre s'écrit:
E(p) = Py
-Px[dB] (III.6)
avec,
· Px est la puissance moyenne du
signal OFDM duobinaire sans l'ajout du signal de réduction du PAPR.
· Py est la puissance moyenne du
signal OFDM duobinaire après l'ajout du signal de réduction du
PAPR.
ClipSeuil
· p = Px est le taux de clipping.
La Figure 3.13 illustre la variation du rapport Py Px
en fonction du taux de clipping p =
ClipSeuil
Px . Où ClipSeuil
étant le seuil de clipping défini à partir du
taux de clipping p.



