- 52 -
Chapitre 3 : Performances de la Nouvelle forme
d'onde

0 5 10 15 20
/Px
Py
0.35
0.25
0.15
0.05
0.3
0.2
0.1
0
ñ=Seuilclip/Px
Figure 3.13: Variation du rapport Py Px en fonction du
niveau de clipping.
On se rend compte, à travers la Figure 3.13 que plus
le seuil de clipping dimunie, plus grand est le rapport Py Px , alors
que Py Px croît avec la puissance totale transmise. Il faut donc
faire un compromis entre la réduction du PAPR et l'augmentation de
l'énergie totale à transmettre.
3.2 Implémentation et processus de
réception
3.2.1 Complexité
Si une méthode est très performante en terme de
réduction du PAPR mais nécessite de fortes ressources de calcul,
ceci peut devenir rédhibitoire pour certaines applications pratiques de
type "temps réel". La complexité des algorithmes mis en oeuvre
doit alors être étudiée. Dans cette section, nous
évaluerons la complexité de la nouvelle forme d'onde et son
processus de décodage. Dans le processus de décodage il faut
considérer
- 53 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
les symboles par paire comme il a été fait
à l'émission. Donc on considère le signal OFDM duobinaire
sur une durée temporelle de 2T, ce qui correspond à 2
symboles OFDM consécutifs. En faisant une transformée de Fourrier
sur chaque paire de symboles OFDM, on décode à l'instant kT
et sur la sous-porteuse i:
· le symbole binaire actuel 2Sk i
· le symbole précédent
Sk-1 i
· le symbole suivant Sk i+1
Ainsi on réçoit :
Rk = 2Sk i +
Sk-1
i + Sk (III.6)
i+1
En supposant que les données traitées par
l'algorithme qui génère la nouvelle forme d'onde sont de taille
NL (où nous supposons que les signaux multiporteuses sont L
fois sur-échantillonnés).
· Le calcul du signal ck, le signal de clipping
a une complexité linéaire, c'est-à-dire, de l'ordre de
O(NL).
· La complexité de calcul du signal
c' k, le signal
d'ajout filtré, est un O(NLlog2NL) car on
utilise un filtrage basé sur les opérations de FFT/IFFT.
· Ayant récupérer Rk, on cherche
à en déduire Sk, le symbole émis. Rk
correspond à une sorte de codage convolutif avec une longueur de
contrainte de deux. Les symboles reçus correspondent à une
transformation selon le système suivant:

Figure 3.14: Système équivalent à la
nouvelle forme d'onde à la réception
où, on peut récuperer les symboles sk i au
moyen d'une égalisation en deux étapes dont la complexité
est linéaire en fonction de N.
- 54 -
Chapitre 3 : Performances de la Nouvelle forme d'onde
Optimisation de la nouvelle forme d'onde Afin
de réduire autant que possible le PAPR, l'algorithme de
génération du signal additionnel doit étre
répeté plusieurs fois selon le processus suivant:
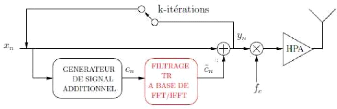
Figure 3.15: Génération du signal
d'ajout.
1. Initialisation considerer le signal OFDM temporel
sn. Initialiser s(i)
k = sn et
fixer i = 0.
2. Calculer le "signal de réduction du PAPR"'
c(i) k en effectuant le clipping de si k à
s'i k, aussi ci k =
-(si k -
s'i
k). Effectuer un filtrage FFT/IFFT pour generer le signal
c'i k .
3. Mettre à jour l'algorithme, c'est-à-dire
si+1 k = ci k + si k.
4. Effectuer une autre itération, si le seuil de PAPR
désiré n'est pas obtenu ou si le nombre d'itération
maximal n'est pas atteint.
Avec cette optimisation, on obtient un énorme gain en
PAPR. Les courbes représentées sur la Figure 3.16 montrent que le
gain de la nouvelle forme d'onde pour 5 itérations, un taux de clipping
= 3dB et celui de la technique de clipping and filtering
classique sont assez proches.
Chapitre 3 : Performances de la Nouvelle forme d'onde

CCDF(ö)=Pr(PAPR >= ö)
100
10-1
10-2
10-3
OFDM Duobinaire
Nouvelle forme d'onde ( ñ=3dB) avec 5 itérations
technique de clipping and filtering classique à 3dB
- 55 -
2 4 6 8 10 12
ö
Figure 3.16: Nouvelle forme d'onde avec un seuil de
clipping à 3dB et 5 itérations.
| 


