à‰tude d'une forme d'onde multiporteuses à faibles variations de puissance

Conclusion

Dans la présente partie, il a été question de situer tout d'abord le contexte de notre étude, qui est de pallier au problème du PAPR. Nous avons ainsi montré que la problématique du PAPR est réelle et que les enjeux environnementaux et économiques sont importants. Aussi, nous avons dans une seconde partie analyser le problème du PAPR des signaux multiporteuses en nous limitant à l'étude de l'OFDM. Nous avons montré l'incompatibilité entre un fort PAPR et un fonctionnement énergétique optimal de l'amplificateur de puissance, qui pourtant consomme le plus d'énergie dans les réseaux sans fil. Enfin, nous avons donné un bref aperçu des méthodes actuels qui permettent de faire face au problème du PAPR, ces méthodes sont à plusieurs égards insuffisantes et ne sont pas optimales. Tout ceci nous amènent à introduire l'idée de la nouvelle forme d'onde qui est une combinaison des techniques traditionnelles de réduction du PAPR (à base d'ajout de signal).

21

CHAPITRE 2

NOUVELLE FORME D'ONDE

Introduction

Dans le premier chapitre, il a été question de l'incompatibilité entre un fonctionnement de l'amplificateur avec un rendement maximal et des signaux multi-porteuses à fort PAPR. Aussi compte tenu des nombreux avantages des signaux multiporteuses, plusieurs efforts de recherche sont effectués pour pouvoir utiliser ces modulations en réduisant au maximum leur PAPR. L'objet de ce chapitre est de détailler une nouvelle forme d'onde qui posséderait tous les avantages de l'OFDM classique et qui aurait un PAPR très faible.

Dans la présente partie, nous exposerons la nouvelle forme d'onde multi-porteuse à très faible PAPR. Cette forme d'onde est une combinaison intelligente de certaines techniques classiques de réduction de PAPR telles que le clipping et la tone reservation, et aussi du codage duobinaire qui reduit le spectre par sous-porteuse de moitié. ^?Pour mieux expliquer cette forme d'onde nous aborderons dans une première partie les techniques de réduction du PAPR à base d'ajout de signal (le clipping et la Tone Reservation). Ensuite, dans une seconde partie, nous étudierons le codage duobinaire. Et enfin dans une troisième partie,nous introduirons notre technique de réduction de PAPR. Cette technique garantit non seulement une réduction considérable du PAPR mais aussi une efficacité spectrale et des performances identiques à l'OFDM classique.

2.1 Techniques de réduction du PAPR

Nous n'éffectuerons pas ici une étude exhaustive des techniques de réduction du PAPR rencontrées dans la littérature, mais nous donnerons un bref aperçu de ces techniques

- 22 -

Chapitre 2 : Nouvelle forme d'onde

en faisant le détail des techniques d'ajout de signal, parce que c'est sur ces techniques que sera notre contribution.

Il existe plusieurs techniques de réduction du PAPR que l'on peut regrouper en trois classes principales :

· les techniques probabilistes qui sont des méthodes ou techniques de réduction du PAPR à représentations multiples du signal et qui ont l'inconvénient de ne pas être à compatibilité descendante¹. On peut citer entre autres le "random phasor" (RP), le "selective scambling", ou le "selective mapping" (SLM), les "Partial Transmit Sequences" (PTS), ou les techniques d'"optimisation de phase", etc [7].

· les techniques de codage sont des techniques de réduction du PAPR qui utilisent des formes particulières de codage afin d'éviter la transmission des symboles qui présentent un PAPR élevé. Tout comme, les techniques probabilistes, elles ont l'inconvénient de ne pas être à compatibilité descendante.[7]

· les techniques d'"ajouts de signal" consistent à ajouter un ou plusieurs signaux appelés "signaux additionnels" ou "signaux de réduction du PAPR" ou encore "signaux correctionnels" au signal d'origine pour atténuer au maximum les variations d'amplitude. Ces techniques sont intéressantes dans la mesure où elles peuvent être à compatibilité descendante [7].

2.1.1 Techniques d'ajout de signal

Comme leur nom l'indique, les techniques "ajout de signal" consistent à ajouter un ou plusieurs signaux appelés "signaux additionnels" au signal original (en général large bande et à fort PAPR) pour atténuer au maximum ses variations d'amplitude. Comme exemples de techniques d'ajout de signal traditionnelles, nous avons la Constellation Extension, la Tone Reservation,[7] . . . Mais bien qu'il ne soit pas aussi trivial, le clipping sous toutes ses formes est une technique d'"ajout de signal" de réduction du PAPR. Le clipping est une technique de "distorsion" et dans le chapitre 4 de sa thèse, Désiré Guel a montré que toute technique de "distorsion" pouvait être formulée comme une technique "ajout de signal", le clipping y compris [7]. Dans cette section, nous étudierons deux techniques d'ajout de signal qui sont le clipping et la Tone reservation, toutes deux seront utilisées dans la nouvelle forme d'onde.

Principe général du clipping

Le clipping dans sa forme la plus simple consiste à un écrêtage de l'amplitude du signal à un seuil prédéterminé. Ce procédé a donc pour effet de diminuer la variation

¹Les méthodes à compatibilité descendantes n'ont pas besoin d'une modification architecturale majeure pour leur implémentation.

Chapitre 2 : Nouvelle forme d'onde

de puissance du signal. La fonction d'écrêtage g[r] du clipping classique qui agit sur l'amplitude r des signaux s'écrit:

{ r si r = A

g(r) = (II.1)
A si r A

A étant le seuil de clipping. Le signal résultant est dégradé et n'aura pas les performances "d'avant clipping" à la réception. Cette technique a été proposée dès le début de la mise en oeuvre de l'OFDM terrestre (DVB-T), dans les années 1997 [7]. De plus, la saturation étant elle-même une opération non-linéaire dont les défauts sous-jacents sont les suivants :

· remontée des lobes secondaires à cause des produits d'intermodulation ce qui génère un bruit hors de la bande utile du signal, encore appélé bruit Out Of Band (OOB).

· Génération de bruit dans la bande utile: bruit qui correspond aux différents termes d'intermodulation qui tombent dans la bande utile, encore appelé bruit In Band (IB).

Pour s'en rendre compte, nous modéliserons l'effet du clipping qui est non-linéaire et sans mémoire, par une transformation polynomiale, représentée comme suit:

y(x) = f0 + f1x+...+ fNx^N (II.2)

où x représente le signal OFDM à écrêter. Dans notre cas x est un signal OFDM, qui est un multiplex de porteuses orthogonales. L'équivalent passe-bas d'un signal OFDM est exprimé comme suit:

x(t) =

N-1 ? k=0

Ikei2ðk ^tT,0 = t <T (II.3)

- 23 -

où Ik sont les symboles de donnée, N est le nombre de sous-porteuses et T la durée du bloc OFDM. En considérant les deux équations II.2 et II.3, on comprend mieux l'apparition des termes d'intermodulations et des harmoniques. Un filtre sélectif en fréquence situé juste après l'écrêtage peut réduire considérablement le bruit OOB. Par contre l'élimination du bruit à l'intérieur de la bande est beaucoup plus subtile mais peut se faire au moyen du filtrage FFT/IFFT.

- 24 -

Chapitre 2 : Nouvelle forme d'onde

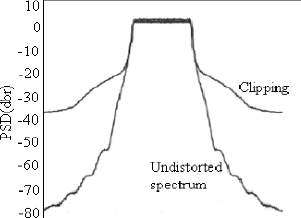
Figure 2.1: Distorsions engendrées par le clipping: remontées des composantes out of band.

La figure 2.1 représente le spectre de l'OFDM avant et après le clipping. On remarque une remontée des parties OOB hors bande utile (le signal utile est situé dans la bande [-20 , 20]). Ceci est dû à la remontée des lobes secondaires des sinus cardinaux qui constituent le spectre du signal OFM, ces différentes rémontées se traduisent par une augmentation de l'ACPR. Ainsi, pour combattre cet effet, l'opération de clipping est toujours associée à une opération de filtrage: on parle de clipping andfiltering. Ce filtrage peut etre effectué par des filtres à base de FFT/IFFT [7]. Le clipping classique, par écrêtage simple n'est pas la seule forme de clipping, il existe d'autres manières d'éffectuer le clipping comme en témoigne la Figure 2.2 tirée de [7].

- 25 -

Chapitre 2 : Nouvelle forme d'onde

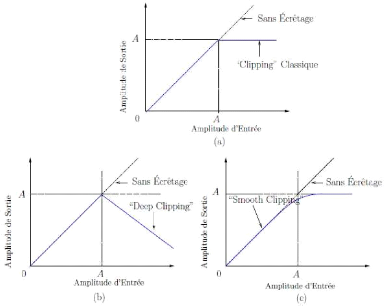
Figure 2.2: Différentes manières d'éffectuer le clipping

Nous pouvons appercevoir dans la Figure 2.2 que d'autres fonctions d'écrêtage beaucoup plus complexes peuvent servir à dimunier la dynamique du signal OFDM. Dans le cadre de ce stage, nous utiliserons uniquement le "clipping classique" parce qu'il est le moins complexe.

2.1.2 Tone Reservation

Cette méthode consiste à réserver un nombre de sous-porteuses du signal OFDM sur lesquelles sera ajoutée de l'information pour modifier le signal temporel, de sorte à diminuer la dynamique de son enveloppe.

- 26 -

Chapitre 2 : Nouvelle forme d'onde

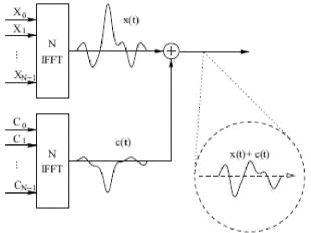
Figure 2.3: Schéma du principe de la Tone Reservation.

Dans cette méthode qui est décrite par la Figure 2.3, l'émetteur et le récepteur s'accordent sur le nombre et les positions des sous-porteuses qui sont réservées pour porter le signal correcteur susceptible de diminuer le PAPR d'ou l'appellation de la méthode : tone reservation. De façon générale, le principe de la tone reservation est comme suit:

Soit X = [ X0,. . . , _XN-1] le vecteur des symboles de données à partir duquel est généré le signal OFDM et soient Ci, i = 0,. . . ,NR les NR symboles pilotes qui seront utilisés pour réduire le niveau de PAPR et avec NR < N. Désignons pas = {i_o,...,NR} l'ensemble des positions des NR symboles pilotes dans le symbole OFDM. Ces sous-porteuses non utilisées serviront à générer le signal de réduction du PAPR, comme le montre la Figure 2.3. Une manière particulière de réaliser la tone reservation qui a été développée par Zabre Sidkièta dans sa thèse [13], consiste à utiliser les porteuses "nulles"; comme par exemple les sous-porteuses réservées pour la synchronisation ou l'égalisation ou eventuellement pour l'annulation du bruit impulsif [6], pour porter le "signal de réduction du PAPR" tout en respectant le gabarit d'émission du standard.

2.1.3 Tone Reservation et clipping

Dans la section précédente, nous avons introduit la notion de clipping ainsi que ses effets néfastes sur le signal. Notre objectif est de nous inspirer de cette technique de réduction

- 27 -

Chapitre 2 : Nouvelle forme d'onde

de PAPR, afin de proposer une autre basée sur un clipping "intelligent" : c'est à dire effectuer le clipping de sorte à n'avoir que ses effets positifs (réduction du PAPR). La manière de réaliser ce clipping sera décrite dans la présente section. Mathématiquement l'opération de clipping correspond bien à un ajout de signal. Considérons par exemple le signal s1 (t) de la Figure 2.4,

Figure 2.4: Clipping au seuil Lclip.

On peut remarquer que écrêter le signal s1(t), est équivalent à lui ajouter le signal -s3(t) (en bleu, sur la Figure 2.4).

Aussi dans le présent stage, l'objectif est d'ajouter le signal -s3(t) en gardant uniquement les composantes fréquentielles qui ne dégradent pas le signal d'origine. Ceci peut être réalisé par la technique Tone Reservation selon le principe suivant:

1. générer toues les composantes fréquentielles de -s3(t).

2. filtrer dans ces composantes fréquentielles générées les fréquences qui dégradent le signal OFDM, c'est à dire les composantes fréquentielles qui coincident aux emplacements des sous-porteuses de données d'une part. Et aussi filtrer les composantes OOB (out of band : les composantes fréquentielles hors bandes) qui

- 28 -

Chapitre 2 : Nouvelle forme d'onde

pourraient se trouver dans le spectre adjacent. Ceci revient à générer à nouveau le signal de clipping avec uniquement les fréquences de -s3(t) qui correspondent aux sous-porteuses libres.

En ajoutant le signal de clipping de façon orthogonale aux signaux de données, nous ne dégradons pas le signal OFDM d'origine, par exemple les performances en terme de TEB sont les mêmes que pour l'OFDM sans clipping.

En résumé, nous avons donc une méthode qui permet de réduire le PAPR et qui à priori n'impacte pas les performances du système (pas de dégradation de TEB). Aussi pour cette méthode nous constatons que le nombre de sous-porteuses d'ajout du signal de clipping n'est pas suffisant. Très souvent, les normes classiques prévoient un nombre réduit de symboles pilotes alors qu'avec la technique de clipping que nous venons de proposer, plus le nombre de pilotes est important, plus grand est le gain de réduction du PAPR.

La question clé est la suivante: comment peut-on obtenir plus de symboles pilotes tout en respectant les exigences de n'importe quelle norme en nombre de symboles pilotes et sans modifier cette contrainte? Le dilemme ici réside dans le fait que si l'on accorde plus de sous-porteuses pour la réduction du PAPR ceci se fera au détriment du débit (dimunition du débit de données utiles). Une solution possible est le codage duobinaire. Dans la Section 2.2, nous détaillerons comment à partir du codage duobinaire, il est obtenu un gain de spectre et donc une réduction plus éfficace du PAPR.

2.2 Dimunition du spectre réalisée par le codage duobi-naire

2.2.1 Codes à réponse partielle: le duobinaire

Nous commençons cette partie par l'introduction du critère de Nyquist pour éliminer complètement l'IES en supposant un échantillonnage idéal.

r(t), le canal global composé du filtre d'émission, du filtre de réception adapté au filtre d'émission, du canal physique, respecte le critère de Nyquist si aux instants d'échantillonnage, le terme IES dans le signal reçu est nul, i.e.,r(t) = 0 pour t = #177;T,#177;2T,#177;3T,...,#177;kT, avec k un entier quelconque. r(0) lui-même doit être non nul. Si le canal global r(t) a un spectre R(f) satisfaisant le critère de Nyquist ci-dessus, alors les échantillons du canal enregistrés à une cadence1 _T sont exemptés d'interférence entre symboles, d'où le critère de Nyquist:

+8

?

n=-8

n

R(f - T ) = T (II.4)

où T est la période des symboles émis.

L'idée des codes à réponse partielle est d'introduire volontairement de l'Inter-Symbol

- 29 -

Chapitre 2 : Nouvelle forme d'onde

Interference (ISI) (IES), de manière contrôlée, pour pouvoir l'interpréter correctement dans le récepteur. L'exemple le plus courant de codes à réponse partielle est le codage duobinaire qui est effectué de la manière suivante:

Considèrons un code binaire ak, c'est-à-dire ak E {0,1}, nous effectuons le précodage des élements binaires ak pour obtenir d'autres éléments binaires bk. Le précodage permet d'éviter la propagation des erreurs. Le précodage considéré permet de générer une séquence binaire bk suivant l'équation suivante:

bk = bk-1 ?ak (II.5)

Ensuite les ik sont obtenus par codage BPSK des bk. Les éléments binaires ik sont transmis à un rythme1 _T . Ils sont transformés à la cadence1 _T en symboles ck appartenant à {-2,0,2} par le codage duobinaire dont le filtre de la transformée est H(z) = 1+z-¹. Le codage duobinaire s'effectue par la transformation

ck = ik +ik-1

. Le canal à réponse impulsionnelle resultant de ce codage duobinaire s'écrit:

h(t) = ä(t)+ä(t -T) (II.6)

Les différentes étapes qui permettent de génerer les éléments duobinaires sont résumées dans la Figure 2.5.

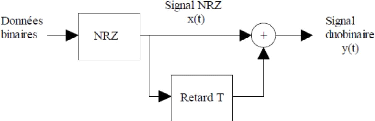
Figure 2.5: Génération des symboles duobinaires.

Le tableau 2.1 donne un exemple de la transmission d'une séquence duobi-naire précodée et la séquence décodée.

Chapitre 2 : Nouvelle forme d'onde

Tableau 2.1: Exemple de codage duobinaire

Séquence binaire ak		0	0	1	0	1	1	0
Séquence précodée bk	1	1	1	0	0	1	0	0
Séquence BPSK ik	+1	+1	+1	-1	-1	+1	-1	-1
Séquence duobinaire dk		2	2	0	-2	0	0	-2
Séquence duobinaire décodée rk		0	0	1	0	1	1	0

L'opération de mise en forme est effectuée par un filtre rectangulaire g(t) de largeur T. On obtient donc:

g(t) = Rect[0,T](t)

s(t) = ?

k

(ik + ik-1)g(t -kT)

(II.7)

Ce signal est aussi égal dans le cas particulier d'un filtre de mise en forme rectangulaire à :

s(t) = ikp(t - kT) (II.8)

p(t) = Rect[0,2T](t) = g(t) + g(t - T)

Il est utile de remarquer ici que le filtre p(t) ne vérifie pas le critère de Nyquist, ceci est voulu. En fait c'est l'étalement temporel de 2T qui engendre la compression de spectre. Avec le précodage, l'effet mémoire introduit par le codage duobinaire est supprimé et la détection à la réception est facilitée et se fait par simple seuillage :

~ 1 si |ck| < 1

rk = (II.9)
0 si |ck| > 1

En l'absence de précodage, pour effectuer le décodage des symboles duobinaires, on doit prendre en compte les décisions passées comme le montre l'équation II.8.

?

???

???

rk =

1 si ck > 1

(II.10)

0 si ck < 1

^drk-1 étant la décision passée.

1 si |ck| ? 1 et ^drk-1 = 0 0 si |ck| ? 1 et ^drk-1 = 0

s(t) = ? ikp(t - kT)

k

p(t) = Rect[0,2T](t) = g(t) +g(t - T)

(II.11)

- 30 -

Densité spectrale de puissance Nous pouvons considérer notre système ainsi constitué comme étant le même qu'une cascade de deux structures de filtres h et g, avec p le canal global dont l'expression est la suivante:

- 31 -

Chapitre 2 : Nouvelle forme d'onde

où g est le filtre de mise en forme.

Ainsi en considérant la fonction de transfert de h qui s'écrit H(f) = 1 ₂(1 + _ej2ð fT) , nous déduisons que l'expression analytique du spectre du signal duobinaire,

S(f) = cos(ð fT)²Tsinc(ð fT)² = T[sinc(2ð fT)]² (II.12)

Nous nous rendons compte ici que le codage duobinaire reduit de moitié le spectre occupé pour un signal BPSK. L'idée alors est d'effectuer cette opération dans chacune des sous-porteuses de l'OFDM. Nous dimunions ainsi pour chacune des sous-porteuses l'occupation spectrale de moitié et on utilise cet espace pour ajouter le signal de réduction du PAPR.

2.3 La nouvelle forme d'onde

Considerons un système OFDM avec N sous-proteuses. Notons par S^(k) = [S^(k)

0 ,...,S(k)

N-1]^t

le kème symbole OFDM (voir Figure 2.6):

- 32 -

Chapitre 2 : Nouvelle forme d'onde

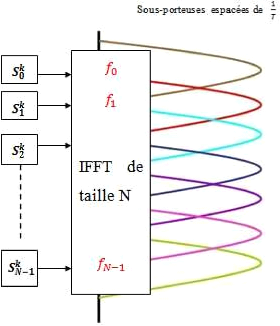
Figure 2.6: Modulateur OFDM classique.

Nous considérons une constellation BPSK, c'est a dire que les symboles S(k)

l , l =

0,...,N sont #177;1. Quand l'on effectue du duobinaire sous-porteuse par sous-porteuse, on aboutit aux conclusions suivantes:

- 33 -

Chapitre 2 : Nouvelle forme d'onde

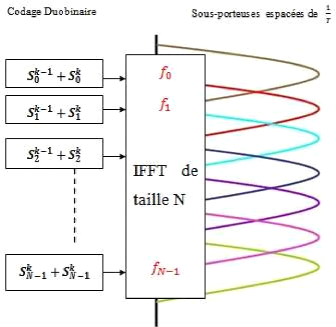
Figure 2.7: Modulateur OFDM Duobinaire

En faisant le duobinaire, on obtient à l'entrée du modulateur OFDM, à l'instant k les symboles S(k)

l +S(k-1)

l , l = 0,...,N, ceci revient à ajouter le symbole OFDM à l'instant
k - 1 à celui de l'instant k (voir Figure 2.7). On garde le même modulateur OFDM à l'émission donc on peut se rendre compte qu'on a toujours d'un point de vu spectral les sinc(sinus cardinaux) qui s'entrecroisent mais qui demeurent orthogonaux. Pour se rendre compte de la réduction spectrale réalisée par le duobinaire, nous traçons les DSP des signaux Duobinaires et ceux binaires(voir Figure 2.8).

- 34 -

Chapitre 2 : Nouvelle forme d'onde

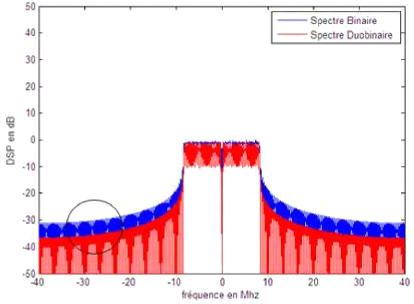
Figure 2.8: DSP binaire et Duobinaire pour N=64 sous-porteuses.

En effectuant un zoom au niveau de la Figure 2.8, on se rend compte que l'espace spectral occupé par chacune des sous-porteuse est réduite de moitié.

- 35 -

Chapitre 2 : Nouvelle forme d'onde

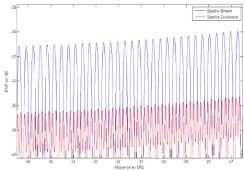
Figure 2.9: DSP binaire et Duobinaire pour N= 64 sous-porteuses zoom.

Alors la question qui nous vient à l'esprit est de savoir où s'effectue alors la réduction de spectre ? Nous allons apporter une réponse, dans la section suivante.

2.3.1 Réduction de spectre pour l'OFDM avec du duobinaire sous chaque sous-porteuse

Où s'effectue alors le gain de spectre?

Considérons le schéma de modulation OFDM illustré par la Figure 2.7. Pour analyser comment se fait la réduction de spectre nous considèrons une succession de quatre symboles OFDM. L'addition du duobinaire se faisant dans le domaine fréquentiel, que se passe t-il alors en temporel?

Tout d'abord, comme l'OFDM est un multiplex de porteuses orthogonales, alors sur 4 temps symboles (c'est-à-dire sur l'intervalle de temps [(k _ 3)T,(k + 1)T]), le signal OFDM peut s'écrire comme:

s(t) =

l=k+1 ? l=k_2

(Sl 0 +Sl_1 0 ) *g(t _kT)e^2j^ðF0t+

(S^l₁ + Sl_1

1 ) *g(t _kT)e2 jð f1t + ... + (SlN_1 +Sl_1

N_1) *g(t _kT)e2 jð fN_1t

où

· T : période des symboles OFDM,

Chapitre 2 : Nouvelle forme d'onde

· N : nombre de sous-porteuses

· g est un filtre rectangulaire c'est-à-dire g(t) = rectT(t)

Nous allons considérer alors le signal modulé par la sous-porteuse f0, puisque le duobi-naire effectue la réduction de spectre sous-porteuse par sous-porteuse. Ce signal qui correspond à la sous-porteuse f0 peut s'écrire pour 4 temps symboles:

sf0(t) =

l=k+1 ? l=k-2

(Sl 0 + Sl-1 0 ) * g(t - kT)e^2j^ðf^0t(II.14)

Posons sl j = S^l je2jð ^f0t sur l'intervalle de temps [jT,(j + 1)T]. On peut réécrire le signal sur la sous-porteuse f0 en temporel comme suit:

Sf0(t) =

l=k+1 ? l=k-2

(Sl 0 +Sl-1 0 ) *g(t -kT)e^2jf^0t=

l=k+1 ? l=k-2

(sl 0 +sl-1 0 ) *g(t -kT) (II.15)

l=k+1

Sf₀(t) = ? al 0 *h(t -kT) (II.16)
l=k-2

où h(t) = rect2T (t). Pour plus de clarté, nous représentons l'évolution temporelle du signal envoyé sur la sous-porteuse f0.

- 36 -

Figure 2.10: Evolution temporelle du signal sur une seule sous-porteuse

On se rend bien compte que:

- 37 -

Chapitre 2 : Nouvelle forme d'onde

· d'une part les symboles OFDM Duobinaires durent T mais ceux binaires durent 2T.

· d'autre part sur un intervalle de temps 2T, de l'interférence vient s'ajouter au symbole binaire, de l'interférence du symbole précédent et celui du symbole suivant (nous détaillerons ce point dans le chapitre 3).

En conclusion nous obtenons des symboles binaires qui durent 2T (une porte rectangulaire de durée 2T) d'où la compression spectrale.