à‰tude d'une forme d'onde multiporteuses à faibles variations de puissance

3

CHAPITRE 1

PROBLÉMATIQUE DU PAPR

Introduction

Les réseaux sans fil consomment de plus en plus d'énergie et contribuent en pourcentage de plus en plus croissant aux émissions de CO2 du secteur des TIC. Ainsi, cet impact climatique mais aussi et surtout les questions de coût sous-jacents tendent à recentrer la recherche dans les communications sans fil vers une recherche de l'optimisation de la consommation d'énergie. Dans le présent chapitre, nous aborderons la problématique du PAPR surtout pour les modulations multiporteuses. Il faut savoir que si l'on cherche des moyens de réduction du PAPR, c'est essentiellement parce que ces modulations multiporteuses très prometteuses ont ce problème de PAPR en commun. Il s'agira essentiellement dans ce chapitre de donner les éléments qui motivent notre recherche des moyens efficaces et économiques qui garantissent une réduction considérable du niveau de PAPR dans les systèmes OFDM, de caractériser le PAPR des signaux multiporteuses, en somme de montrer le besoin de réduction du PAPR pour des communications dites green ou vertes. Ce chapitre est organisé comme suit:

· dans une première section, après avoir établi la nécessité d'un gain en PAPR pour les systèmes actuels et futurs, nous analyserons les modulations multiporteuses. Nous verrons la radio-intelligente qui pourrait rencontrer aussi ce problème de PAPR. Nous étudierons essentiellement le PAPR de l'OFDM qui est la modulation multiporteuse la plus populaire pour ses multiples avantages.

· Puis dans une seconde section, nous décrirons le PAPR, nous illustrerons les approximations rencontrées dans la littérature de la distribution du PAPR.

· Enfin, nous aborderons les solutions courantes proposées dans la littérature, qui jusque là permettent de pallier au problème du PAPR.

- 4 -

Chapitre 1 : Problématique du PAPR

1.1 Reduire la consommation énergétique des TIC.

1.1.1 Contribution des réseaux sans fil à la consommation énergétique des TIC.

L'optimisation de l'efficacité énergétique des TIC doit se faire à tous les niveaux, pour tous les types de réseaux et de services télécom. Aussi notre étude concerne surtout les réseaux sans fil qui sont un grand contributeur à la consommation globale d'énergie des TIC.

Selon une étude ménée par SMART 2020 (intitulée : enabling the low carbon economy in the information age), qui est un groupe de travail sur les changements climatiques, les émissions en C02 provenant des TIC représenteraient 530 mégatonnes de CO2 en 2002 et 830 mégatonnes en 2007. C'est environ 2% des émissions humaines de CO2 et équivalent à ceux de l'aviation mondiale [2]. Dans les TIC, la contribution de la communication mobile était de 64 mégatonnes de CO2 en 2002. Cela peut paraitre assez faible (12% des émissions de TIC), mais il devrait croître de près d'un facteur de trois à 178 mégatonnes en 2020 avec l'augmentation du trafic de données sans fil et avec le déploiement de stations de base supplémentaires pour la prochaine génération (4G) des réseaux mobiles. La fraction la plus importante des émissions de CO2 se produit dans le réseau d'accès. Comparée à cette consommation, l'énergie consommée (et les émissions de CO2 qui vont avec) à la fois par les appareils mobiles et des serveurs dans le réseau de base est plus faible d'un facteur de 4 ou 5 [4].L'infrastructure d'accès sera donc la clé des "Green ICT", des communications plus efficientes énergétiquement.

Le problème de l'efficacité énergétique même s'il n'est pas tout à fait nouveau, a eu un regain d'intérêt depuis ces dernières années surtout avec les modulations mul-tiporteuses. Comme en témoigne l'établissement du consortium EARTH dont l'ojectif est de reduire la consommation énergétique des TIC. EARTH vient de l'accronyme Energy Aware Radio and Network Technologies. Le consortium EARTH est composé d'institutions académiques de haut niveau, de prestataires de services en télécommunications et de fournisseurs de composants et d'infrastructures; il espère pouvoir réduire la consommation énergétique de 50% d'ici fin 2020. Le projet souhaite réduire les émissions de dioxyde de carbone (CO2) dans le secteur des TIC et faciliter la mise en oeuvre de services sans fil à large bande respectueux de l'environnement.

Ce stage s'addresse surtout à l'optimisation de l'efficacité énergétique au niveau des réseaux sans fil, et plus particulièrement au niveau du réseau d'accès.

La Figure 1.1 permet de mieux comprendre la répartition de la consommation d'énergie dans les réseaux sans fil, ceci nous permet de nous apercevoir plus aisement des parties du réseaux les plus "gourmands" en énergie.

- 5 -

Chapitre 1 : Problématique du PAPR

Réseaux sans fil % TICS 12%

réseau
d'accès %
Réseaux
sans fil
57%

Ampli
ficateurs
% BTS
65%

Matériel
Fourniture
en énergie

Module Traitement de signal

Figure 1.1: Répartition de la consommation d'énergie dans les réseaux sans fil

Nous montrons à travers la Figure 1.1 que l'intérêt pour l'étude de l'amplificateur de puissance n'est pas fortuit. En effet au niveau des composants, un énorme potentiel d'économie d'énergie peut être obtenu grâce aux amplificateurs de puissance.

Chapitre 1 : Problématique du PAPR

Amplificateurs

65%

7.5%

Fourniture d'énergie

10%

Traitement signal

17.5%

- 6 -

Circuits de Refroidissement

Figure 1.2: Répartition de la consommation d'énergie par composants pour les stations de base.

La Figure 1.2 confirme bien que la plus grande consommation d'énergie dans les stations de base se trouve au niveau des amplificateurs de puissance. Réduire la consommation d'énergie des réseaux sans fil passe donc par une optimisation énergétique des amplificateurs de puissance.

1.1.2 Amplificateur de puissance.

L'amplificateur est un élément non linéaire de la chaine de communication. Il est caractérisé par ses relations entrées-sorties AM/AM (pour "Amplitude/Amplitude") et AM-PM (pour "Amplitude/Phase") appelées aussi caractéristiques de transfert ou conversions AM/AM et AM-PM, qui ont une allure typique pour tous les amplificateurs de puissance à l'état solide [9]. La caractéristique AM/AM de l'amplificateur de puissance se divise en trois zones :

· zone linéaire: dans cette zone, l'amplificateur a un comportement linéaire. La

- 7 -

Chapitre 1 : Problématique du PAPR

puissance de sortie est proportionnelle à la puissance d'entrée selon un rapport appelé gain de l'amplificateur. Les puissances d'entrée sont faibles dans cette zone, mais les distorsions engendrées sont quasi inexistantes. Pour éviter les distorsions, on a intérêt à avoir des amplicateurs qui fonctionnent dans cette zone linéaire.

· zone de compression: dans cette zone, la sortie n'est plus proportionnelle à la puissance d'entrée. La courbe commence à s'incurver, on amorce la plage de la non-linéarité. Les distorsions du signal apparaissent et sont de plus en plus importantes.

· zone de saturation : dans cette zone, la puissance de sortie est quasi constante quelle que soit la puissance d'entrée. On parle alors de puissance de saturation. On cherchera à éviter cette zone car cette zone engendre une distorsion dramatique du signal.

Notion de rendement

Un amplificateur de puissance est un dispositif transformateur d'énergie, présentant deux entrées et une sortie : les entrées d'alimentation et de signal à amplifier, et une sortie pour le signal amplifié. L'alimentation de l'amplificateur fournit une puissance totale _Pdc, qui idéalement devrait être entièrement convertie en puissance utile P_s, sans perte de conversion. Malheureusement, en réalité, il faut aussi considérer une puissance de pure perte _Pdiss dissipée au sein de l'amplificateur, comme indiqué sur le schéma de bilan de puissance de la Figure 1.3.

Puissance d'alimentation

Puissance de sortie

Ps

Pdc

Pdiss

Puissance dissipée

Puissance d'entrée

Pe

Figure 1.3: Bilan de puissance de l'amplificateur.

On parle de rendement énergétique ou rendement de puissance pour donner une mesure de la quantité _Pdc qui a été effectivement convertie en P_s. Les valeurs de rendement fournissent une information à propos des pertes _Pdiss. Le rendement DC, est défini

- 8 -

Chapitre 1 : Problématique du PAPR

comme le rapport entre la puissance P_s fournie à la charge (l'antenne en l'occurrence), et la consommation DC de l'amplificateur. La consommation en énergie d'un amplificateur de puissance est étroitement liée à son rendement, il est donc important de faire fonctionner l'amplificateur avec le plus grand rendement possible. Cependant, un amplificateur de puissance fonctionnant à rendement maximal se trouve proche de la zone de non-linéarités (voir Figure 1.4 ).

Figure 1.4: Caractéristique d'un ampli~cateur de puissance intégrant rendement et non linéarités

La Figure 1.4 montre la caractéristique d'un amplificateur de puissance intégrant rendement et non-linéarités. On peut se rendre compte que plus le rendement est grand, plus on est proche de la zone de non-linéarités. En outre en étant proche de cette zone de non-linéarités, il faudrait des signaux qui aient une faible dynamique afin que leurs éventuelles fluctuations n'amènent pas le signal dans la zone non linéaire. On comprend bien que l'amplificateur à rendement optimal se concilie mal avec les signaux à grande dynamique tels que les signaux multiporteuses.

On voit sur la Figure 1.4 que le rendement de l'amplificateur de puissance est maximal dans sa zone de saturation. Malheureusement c'est dans cette zone que les signaux à forte dynamique de type multiporteuses (généralement à fort PAPR) subissent le plus la

- 9 -

Chapitre 1 : Problématique du PAPR

non-linéarité de l'amplificateur.

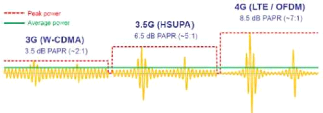
Figure 1.5: Evolution de la dynamique des signaux radio mobile au fil des générations.

La Figure 1.5 illustre l'évolution du PAPR au fil des générations de réseaux radio mobile. Le PAPR est au plus bas avec les modulations de la 2G(GSM), et augmente pour être à son maximum avec l'adoption des modulations multiporteuses de type OFDM (4G).

1.2 Modulations multiporteuses

Les techniques dites multiporteuses consistent à transmettre des données numériques en les modulant sur un grand nombre de porteuses en même temps. Ce sont essentiellement des techniques de multiplexage en fréquence. La plus répandue de ces modulations multiporteuses est l'OFDM. C'est ce type de modulation que nous avons considéré dans notre travail.

L'OFDM est utilisée dans plusieurs standards de communication. On peut citer entre autre, l'ADSL, le WiFi le WIMAX appartenant à la famille du standard IEEE 802.xx et permettant la transmission de données sans fil haut débit. L'OFDM est aussi utilisée dans la DAB, dans la DVB et dans le LTE pour la future norme de réseau mobile 4G [3].

Si le problème d'éfficacité énergétique se pose déja pour les systèmes OFDM, c'est surtout pour ceux à venir (5G¹) à base de transmissions multistandards, de la radio réalisée par logiciel SDR, d'accès dynamique du spectre (Dynamique Spectrum Access). . . C'est aussi pour cette génération de radio mobile pour lequel persiste également le problème de l'efficacité énergétique des modulations multiporteuses, que réside l'intérêt d'une étude sur le PAPR.

¹la 5G est le nom générique de la future génération radio mobile qui succèdera à la 4G

- 10 -

Chapitre 1 : Problématique du PAPR

1.2.1 Radio intelligente

Actuellement, nous sommes en présence de plusieurs standards de communication souvent incompatibles entre eux. La multiplicité des standards de télécommunication fait apparaître la nécessité de disposer de terminaux multistandards et reconfig-urables. Ces nouvelles fonctionnalités trouvent leurs réponses dans le domaine de la radio logicielle, c'est à dire la radio réalisée par logiciel (par la seule modification du logiciel embarqué, on peut changer de standard de communication).

De tels terminaux ne sont pas encore réalisables pour des raisons technologiques liées à la complexité nécessaire à leur réalisation (convertisseurs ultra rapides, processeurs reconfigurables, antenne très large bande,....).

En se basant sur une véritable technologie radio logicielle, la radio intelligente va encore plus loin dans la prospective en dotant le terminal de capteurs qui lui permettront de s'adapter et de réagir vis à vis de son environnement. La radio devient alors décentralisée et flexible se détachant de la notion de standards, pouvant par exemple transmettre de façon opportuniste une communication dans une bande qui aura été détectée comme libre. Le capteur spectre dont l'objectif est de déterminer la ressource spectrale disponible pour transmettre une communication dite "opportuniste". Cet accès opportuniste au spectre, en permettant la transmission sur une large bande de spectre peut surtout genérer des signaux à fort PAPR. La 5G qui viendra après la 4G, pourrait introduire le concept de radio intelligente dont l'objectif est de permettre une radio capable d'être alerte face à son environnement. Cette radio doit être en mesure d'observer les conditions de son environnement (grâce à des capteurs) les conditions en matière de ressources spectrales, de standards disponibles,...; de prendre des décisions en fonction de ses observations et de modifier son fonctionnement en conséquence. Joe Mitola qui est à l'origine de la "Sofware Define Radio" définit le "Cognitif Cycle" en six étapes:

· observe: Prendre conscience de l'environnement (par exemple de ses caractéristiques en matière de ressources spectrales disponibles).

· Orient: Orienter le traitement selon divers niveaux de priorité (normal, urgent,immédiat).

· Plan: Planifier les meilleures configurations possibles suivant les priorités précédentes.

· Decide: Allouer les ressources.

· Act: Effectuer la reconfiguration de l'équipement.

· Learn: Apprendre des échecs ou des réussites des précédentes reconfigurations

[8]

Chapitre 1 : Problématique du PAPR

Ce projet de fin d'études a été réalisé au sein du laboratoire SCEE², qui depuis plusieurs années s'est spécialisé dans l'étude de la radio intelligente. En outre la présente étude concerne essentiellement l'aspect gestion énergétique de la radio intelligente, comment en prévision de leur deploiement, augmenter l'efficacité énergétique des futurs réseaux (5G) qui seront multi-standards, multi-modes et qui auront par défaut un PAPR élévé. Nous citerons ici le travail de SAJJAD Hussain qui a montré une certaine équivalence gaussienne entre un signal OFDM et un multiplex de porteuses multistandards [8]. Dans le paragraphe suivant, nous montrerons l'équivalence entre les signaux de la radio-intelligente qui sont des signaux multi-standards et les signaux OFDM. Cette équivalence nous permet d'approximer le PAPR des signaux de la radio-intelligente par celui de l'OFDM.

Soit x(t) un signal composé de S standards Si(t) (i = 1,...,S). x(t) est alors exprimé comme :

S

x(t) = ? Si(t) (I.1)

i=1

Le signal x(t) sera qualifié de composite. Chaque signal Si(t) est associé à un standard composé de Pi porteuses. Un signal Si(t) s'exprime alors par :

Pi

Si(t) = ? ri_,p(t)e^2iðf^i,p^t. (I.2)
p=1

Ici _ri,p(t) représente la réponse complexe utile du signal après filtrage et modulation sur la porteuse p dans le standard i. Dans ce cas, ri,p(t) = femi(t)*mi_,p(c(t)) , où mi_,p(c(t)) et femi(t) représentent respectivement les fonctions de transfert de la modulation et du filtre de mise en forme, pour la porteuse p et le standard i. On en déduit alors que:

x(t) =

S ? i=1

Pi ? p=1

femi(t) *mi,p(c(t))e^2iðf^i,p^t. (I.3)

L'équation I.3 définit ainsi l'expression générale d'un signal multi-standard appelé encore signal radio logiciel. On peut remarquer une équivalence analytique entre un signal multistandard et un signal OFDM (l'écriture d'un symbole est donné par l'équation I.12. Si l'espace entre les porteuses _fi,p est constant (= ä p) pour tous les standards considérés, le signal radio logiciel défini dans l'équation I.3, s'écrit :

x(t) =

S ? i=1

Pi ? p=1

ri,p(t)e^2ið((p^-^1)äp^)t (I.4)

- 11 -

²Signal, Communication et Electronique Embarquée: SCEE est une équipe de recherche du Campus de Rennes de Supélec, membre de l'IETR (Institut d'Electronique et de Télécommunications de Rennes - UMR CNRS 6164), groupe AC (Automatique et Communications)

- 12 -

Chapitre 1 : Problématique du PAPR

Une hypothèse forte en OFDM réside dans le fait que tous les échantillons du signal modulé suivent un loi normale centrée et de variance donnée. Ceci est dû au théorème de la limite centrale, en supposant que les symboles qui effectuent la modulation OFDM sont indépendants et suivent la même loi.

En extrapolant cette hypothèse à un signal radio logicielle et toujours en vertu du théorème de la limite centrale, les échantillons du signal x(t) de l'équation I.3 suivent une loi normale. La fonction de répartition du PAPR d'un signal radio logiciel est alors équivalente à celle d'un signal OFDM I.4. Cette équivalence démontrée par SAJJAD Hussain dans sa thèse "Peak to Average Power Ratio Analysis and Reduction of Cognitive Radio Sig-nals"[8], va être utilisée lors de notre travail et nous allons donc étudier uniquement le PAPR des signaux OFDM.

1.2.2 OFDM: Orthogonal Frequency Division Multiplexing

L'OFDM est la plus populaire des modulations multiporteuses à cause d'une part de son implémentation facilitée par les opérations IFFT/FFT et aussi de son usage optimal du spectre. Néamoins l'OFDM possède des inconvénients qui sont le problème de synchronisation et aussi et surtout son fort PAPR. Dans cette section nous allons tout d'abord introduire cette modulation, sur laquelle sera basée notre étude du PAPR, ensuite nous analyserons les distributions du PAPR d'une telle modulation.

L'idée maitresse dans la formation du signal OFDM est l'usage d'un multiplexage fréquentiel de sous-porteuses sous certaines conditions d'orthogonalité qui permettra essentiellement d'éviter l'interference entre les symboles (IES). Le multiplexage consiste à repartir l'information à transmettre à fort débit sur un grand nombre de sous bandes modulées à bas débit. Contrairement aux systèmes FDM classiques, où les sous bandes OFDM se chevauchent, mais une condition d'orthogonalité permet d'éviter l'interférence entre les sous-porteuses. Cette contrainte est définie d'un point de vue fréquentiel (choix de l'écart entre les sous-porteuses) mais aussi d'un point de vue temporel (choix de la fonction de mise en forme) à cause de la dualité temps fréquence. La fonction de mise en forme la plus utilisée est la fonction porte où l'écart entre les sous-porteuses est donné par:

Äf = 1 TS où TS est la durée d'un symbole OFDM utile. Ainsi les N fréquences porteuses possibles sont définies par la rélation suivante:

k

fk = f0 + (I.5)
TS

où k = 0...N - 1 et f0 est la fréquence centrale.

Soient _Øn,k une base de signaux élémentaires définis pour k variant de 0 à N -1 et pour

Chapitre 1 : Problématique du PAPR

n variant de -8 à +8 par la relation :

Øn,k = gk(t - nTS) (I.6)

tel que:

gk(~

ej2ðfkt si 0 < t < TS ( )
t) = 0 si t > TS I.7
La base ainsi construite est orthogonale. Le signal OFDM est alors décrit comme:

e(t) =

+8 ? n=-8

N-1 ? k=0

Ck(n)Øn,k(t) (I.8)

avec Ck(n) représentant le symbole complexe à transmettre sur la k ^ieme sous-porteuse du n^symbole OFDM. Á partir des équations I.8 et I.7, nous pouvons écrire:

e(t) =

+8 ? n=-8

N-1 ? k=0

Ck(n)ej2ðf0tej2ð ^TSk (t-nTS)gk(t -nTS) (I.9)

La réalisation analogique d'un modulateur OFDM peut sembler complexe, puisqu'il faudrait en toute logique N modulateurs, bien synchronisés, et dont les fréquences sont espacées d'exactement ¹_TS. Si l'on considère et sans perte de généralités un seul symbole OFDM, l'enveloppe complexe du signal émis s'écrit:

e(t) =

N-1 ? k=0

Ck(n)ej2ðf0tej2ð TS k (I.10)

- 13 -

Il est important de noter ici que la relation I.10 peut ètre réalisée grace à la transformée de fourier discrète Inverse (TFDI ou IDFT Inverse Discrete Fourier Transform) et peut ètre implémentée facilement à l'aide de la TFR (Transformée de Fourier Rapide, en englais FFT Fast Fourier Transform). Comme le montre la Figure 1.6, les symboles sont d'abord réunis pour former un vecteur de N élements par une transformation série parrallèle. Ensuite chacune des composantes de ce vecteur module une sous-porteuse OFDM; ceci est effectué au moyen de l'opération IFFT.

- 14 -

Chapitre 1 : Problématique du PAPR

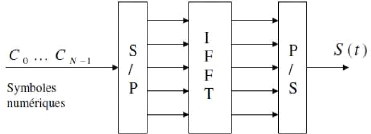
Figure 1.6: Modulateur OFDM numérique.

La démodulation se fait par une transformée de fourier (FFT) du signal reçu et échantilloné au rythme TS (voir Figure 1.7).

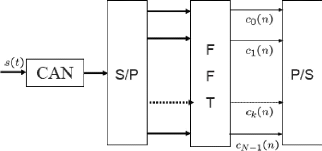
Figure 1.7: Démodulateur OFDM numérique. Les avantages de l'OFDM sont nombreux:

· une utilisation efficace des ressources fréquentielles en comparaison avec les solutions traditionnelles de multiplexage fréquentiel.

· Une égalisation numérique et un décodage simple et optimal grace à l'utilisation de l'intervalle de garde.

- 15 -

Chapitre 1 : Problématique du PAPR

· Les techniques multiporteuses sont robustes au bruit impulsif puisque chaque sous-porteuse est affectée d'un bruit indépendant des autres sous-porteuses. Contrairement aux modulations monoporteuses où le bruit peut affecter un certain nombre de symboles transmis, la perte d'un symbole dû à un bruit important n'affecte pas les autres symboles [5].

· Enfin, il est à noter que l'estimation du canal dans le contexte OFDM est possible et se fait généralement par l'envoi de séquences d'apprentissage dans le domaine fréquentiel.

L'OFDM ne possède pas que des avantages. En effet l'OFDM est très vulnérable aux problèmes de décalage en fréquence (frequency offset) et de synchronisation. Dans le premier cas, le frequency offset engendre de l'interférence entre sous-porteuses (ICI Inter-Carrier Interference) qui peut détruire l'orthogonalité des sous-porteuses. Dans le second cas, les erreurs de synchronisation induisent un déphasage sur les symboles reçus (ISI Inter-Symbol Interférence) [5]. Aussi, l'un des principaux inconvénients du signal OFDM est le fait qu'il a une grande dynamique, ce qui engendre des symboles temporels à fortes variations d'amplitude (à PAPR élevé). Le signal OFDM est très sensible aux non-linéarités des composants analogiques, et surtout incompatible avec un fonctionnement énérgétique optimale des amplificateurs de puissance. D'où l'intérêt de trouver des solutions économiques et à complexité réduite qui garantissent des signaux OFDM avec un niveau de PAPR réduit.

1.3 PAPR des signaux multiporteuses de type OFDM

Définition du PAPR

J.Palicot et Y. Louet ont proposé dans [11] une généralisation de la définition du PAPR. Aussi dans le cadre de ce stage la définition adoptée à été celle du PAPR des signaux en bande de base et en émission. On peut definir le PAPR comme étant une mesure de la dynamique ou de la quantité de fluctuations d'amplitude des signaux. Il est défini comme étant le rapport de la puissance crête (ou puissance instantanée maximale) d'un signal sur la puissance moyenne de ce signal. Le PAPR du signal OFDM s(t), est défini par l'expression suivante: :

PAPR([s]) =

max s(t) 2 0=t=Ts (I.11) Ps

où max s(t) ² est la puissance crête et P_s est la puissance moyenne. Soit s(t) un signal OFDM sur-échantillonné à une fréquence fs = NL/Ts, où L est le facteur de sur-échantillonnage, N le nombre de sous-porteuses et T_s est le temps symbole. Soient

Chapitre 1 : Problématique du PAPR

s_n,0 = n = NL les échantillons de s(t), c'est-à-dire :

1

N-1

?

k=0

_vN

s_n =

Cke( j2ðkn

N ) (I.12)

et on a aussi :

max |s_n|²

^0=n=NL(I.13)

PAPR([s]) =

E(|s_n|²)

max |s_n|²

0=n=N

= ø] = 1

P

2 (I.15)

Pr[^|PS = ø],

= Pr[

N-1

?

n=0

S

- 16 -

où C_k réprésente l'élément modulé sur la sous-porteuse k et sachant que P_s = E(|s_n|²) avec E désigne l'espérance mathématique.

1.3.1 Distribution du PAPR des signaux OFDM

Le signal OFDM est une combinaison linéaire de N variables indépendantes et identiquement distribuées. C'est donc une variable aléatoire ayant de grandes variations d'amplitude. Le PAPR d'un signal étant de fait une variable aléatoire, une étude statistique s'impose. Ceci passe par la détermination de la distribution (fonction de répartition) du PAPR. D'après le théorème de la limite centrale, le signal discret OFDM bande de base (facteur de sur-échantillonnage=1), s_n, défini par l'équation I.12 converge vers une distribution Gaussienne complexe pour un nombre de sous-porteuses, N assez élévé. Par conséquent, l'amplitude du signal OFDM converge vers une distribution de Rayleigh pour de grandes valeurs de N comme l'illustre la fonction densité de probabilité de l'amplitude de s_n qui s'écrit comme suit :

2r r2

P_s(r =|s_n|) = _e-Ps ,r = 0 (I.14)
P_s

où P_s = E(|s_n|²) est la puissance moyenne du signal OFDM discret. La fonction de répartition du PAPR connu sous le nom de CCDF ("Complementary Cumulative Distribution Function") est égale :

CCDF[_s](ø) = Pr[PAPR = ø]

Chapitre 1 : Problématique du PAPR

en considérant l'indépendance entre les symboles s_n. Comme, |s_n| est une variable aléatoire de Rayleigh dont la fonction densité de probabilité est donnée par l'équation

I.14 alors,

2 ~_\/øPS

Pr[^|PS = ø] = Pr[|s_n| = \/øPS = Jo p_s(r)dr (I.16)

En substituant l'équation I.16 dans l'équation I.15, la CCDF du PAPR du signal OFDM discrétisé à la fréquence de Nyquist (c'est-à-dire pour un facteur de sur-échantillonnage L = 1) vaut:

CCDF[_s](ø) = 1 - (1- e^-ø)^N (I.17)

Cette expression de la CCDF du PAPR a été prouvée pour la première fois par R. van Nee et A. de Wild [12]. De l'équation I.16, on peut calculer la fonction densité de probabilité du PAPR qui vaut :

?

p[PAPR](ø) = CCDF[_s](ø) = Ne^-ø(1 -e^-ø)^N-1 (I.18)
?ø

Il a été montré par H. Ochiai et H. Imai [10] que la valeur moyenne du PAPR vaut :

(I.19)

+8

E[PAPR] =

f øp[PAPR](ø)dø

_i

_=N

_J+~ øe^-ø(1 -e^-ø)^N-1dø

1

~= Ceuler +ln[N]

oÙ _CEuler est la constante d'Euler-Mascheroni utilisée principalement en théorie des nombres, définie comme étant [7]:

CEuler = lim [ N?+8

N ? k=1

1 k

- ln[N]] ~= 0.57721. (I.19)

- 17 -

La distribution du PAPR obtenue en I.16 n'est pas une distribution exacte du PAPR du signal OFDM continu, c'est une valeur approchée du PAPR de l'OFDM à la fréquence de Nyquist (facteur de sur-échantillonnage de 1). Il existe des développements de la distribution du PAPR du signal OFDM continu (facteur de sur-échantillonnage supérieur à 1) bande de base qui sont déterminés soit de facon empirique ou soit de facon analytique. R. van Nee et A. de Wild [10] proposent une formule empirique de la CCDF du PAPR pour un signal OFDM continu bande de base :

CCDF(ø) ~= 1 - (1 - e-ø)2.8N (I.20)

Par la suite, Ochiai et Imai ont proposée une approximation de la distribution de la CCDF du PAPR [7]:

( 1 si ø = ø

CCDF(ø) ~= 1- (1 - vøe- 4-1 )v3Nvøe ^ø (I.21)

vø_e-ø

sinon

- 18 -

Chapitre 1 : Problématique du PAPR

ø étant le paramètre qui influe sur l'acuité des résultats, on peut optimiser les résultats en fonction de ø. Les meilleures performances obtenues par Ochiai et Imai étant pour ø ð. Plus tard, Zhou et Caffery dans [14] proposent une borne supérieure pour la

CCDF du PAPR :

r ð

CCDF(ø) = 3 Nvøe^-ø (I.22)

Y. Louet et S.Hussain ont proposé dans [7] une nouvelle fonction de distribution du PAPR des signaux continus OFDM en bande de base.

CCDF(ø) ~= 1 -(1 -eø)^ô2Nì ,ô2 = (5.12 ve ₎ì e-0.5704, ì = 1.07 (I.22)

et N est le nombre de sous-porteuses du symbole OFDM.

1.4 Solutions possibles au problème du PAPR

1.4.1 Formes d'onde à PAPR très faible: GMSK

Il existe des modulations dont le PAPR est nul ou très faible. C'est le cas des modulations à enveloppe constante comme le GMSK utilisé dans le GSM. Et plus généralement les modulations de phase. Comme l'information n'est pas transportée par l'amplitude, ces modulations ont une amplitude constante donc un PAPR très faible en bande de base. On peut donc amplifier ces signaux en se mettant au point de saturation, ce qui évitera tout traitement de non-linéarités et avec un rendement maximal de l'amplificateur.

X(t) = Acos(ù_pt + ö(t)) (I.23)

avec ö(t) = K_p * m(t) et m(t) est le signal modulant.

Le GMSK est certes à PAPR très faible mais son exploitation du spectre n'est pas optimal, la nouvelle forme d'onde étudiée dans ce stage devrait avoir un PAPR très faible comme celui du GMSK mais conserver tous les avantages que l'on connait à l'OFDM.

1.4.2 Techniques de réduction du PAPR

Ce sont des techniques qui agissent sur le signal de sorte à dimunier sa dynamique. A la sortie on obtient un signal à PAPR réduit. Une multitude de techniques a été developpée. Nous ne ferons pas ici un état de l'art de toutes les techniques de réduction du PAPR, mais il convient de remarquer que d'une part aucune des techniques développées jusqu'à ce jour n'arrive à réduire complètement le PAPR, en plus la majorité des techniques de réduction du PAPR ne sont pas à compabilité descendante (c'est à dire que pour les

- 19 -

Chapitre 1 : Problématique du PAPR

utiliser nous avons besoin de faire une mise à jour matérielle des équippements qui les implémentent, disons des systemes reconfigurables), en outre la pluspart des techniques de réduction du PAPR introduisent soit des distorsions sur le signal (dégradations du TEB, remontée du spectre hors bande,...) soit induisent une baisse de débit à cause de l'information de biais (side information) nécessaire à leur mise en oeuvre. Néamoins la technique basée sur la nouvelle forme d'onde s'inspire de certaines techniques traditionnelles de réduction du PAPR notamment les techniques d'ajout de signal que nous détaillerons dans le chapitre 2.

1.4.3 Recul d'entrée et de sortie de l'amplificateur

Cette solution consiste à utiliser l'amplificateur dans sa zone de fonctionnement linéaire. Pour cela, on surdimensionne l'amplificateur et on s'éloigne ainsi de la zone non-linéaire. C'est actuellement la solution la plus utilisée par de nombreux systèmes pour éviter les problèmes de PAPR.

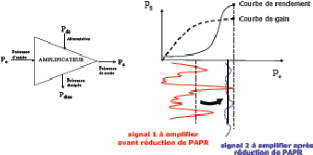
Figure 1.8: Caractéristique d'un ampli~cateur de puissance intégrant rendement et non linéarités

On se rend vite compte que cette solution n'est pas très optimale car dans la zone linéaire l'amplificateur a un rendement très bas donc une importante consommation d'énergie.

1.4.4 Les méthodes qui portent sur l'amplificateur

On peut aussi mettre en place des dispositifs qui agissent sur l'amplificateur pour modifier son fonctionnement. Certaines techniques, comme la contre-réaction, l'approche

- 20 -

Chapitre 1 : Problématique du PAPR

feedforward ou la pré-distorsion agissent sur l'amplificateur. Le principe de la pré-distorsion par exemple est de pré-déformer le signal pour compenser les distorsions ultérieures dûes à l'amplificateur.

A titre d'exemple, un circuit de prédistorsion analogique est conçu pour générer à une fréquence donnée, des courbes de conversions AM/AM et AM/PM inverses à celle de l'amplificateur de puissance à linéariser. Ainsi on peut augmenter le rendement de l'amplificateur sans toute fois tomber dans les zones de non-linéarité.

La technique utilisée dans ce stage relève plutôt de la première catégorie de techniques pour pallier au problème du PAPR, en fait l'objectif de ce stage est d'étudier une nouvelle forme d'onde OFDM qui aurait un PAPR très faible et réglable.