3.6. Simulations
Dans ce qui va suivre, nous allons présenter les
différents résultats de simulation obtenus avec les lois de
commande élaborées précédemment pour le
modèle de la suspension active quart de véhicule.
3.6.1. Résultats de simulation LQR
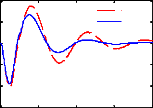
Les figures 3.5, 3.6 montrent les réponses
fréquentielles et temporelles des critères. Le test temporel
simule le passage sur une bosse d'amplitude maximale de 5cm. Ce test permet
d'analyser la sensibilité du système contrôlé en
présence de perturbations en entrée.
L'entrée de perturbation correspondant au profil de la
route est donnée par l'équation :

Diagramme de Bode du transfert Yacc(s)/w (s)
102
passif
101
actif
100
10-1
100 101
Magnitude (abs)
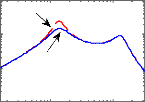
Diagramme de Bode du transfert Ypneu(s)/w (s)
1
passif
10-2
actif
10-3
100 101
Magnitude (abs)
10-
Frequence (Hz) Frequence (Hz)
|
Magnitude (abs)
|
100 10-1 10-2
10-3
|
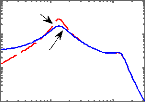
Diagramme de Bode du transfert Ysusp(s)/w (s)
100 101
passif
actif
Frequence (Hz)
Figure 3.5 - Critères fréquentiels du
modèle quart de véhicule

51
|
Amplitude (rn/s2)
|
0.4
0.2
0 -0.2 -0.4
|
|
Amplitude (m)
|
4 2 0 -2 -4 -6
|
Accélération Verticale de Caisse
passif actif
0 0.5 1 1.5 2
temps (s)
x 10-3 Débattement de suspension
x 10-4 Ecrasement du pneu
passif actif
0 0.5 1 1.5 2
tamps (s)
Force de contrôle
Amplitude (N)
-10
-20
-30
10
0
passif actif
Amplitude (m)
-2
-4
4
2
0
passif actif
0 0.5 1 1.5 2
temps (s)
0 0.5 1 1.5 2
temps (s)

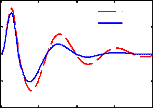
Figure 3.6 - Réponses temporelles du modèle quart
de véhicule avec le contrôleur LQR à
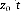
l'excitation ( )
D'après la figure 3.5, on observe que la loi de
commande obtenue permet effectivement d'amortir la résonance de la masse
suspendue autour de 1 Hz, ce qui améliore sensiblement les performances
(confort en basse fréquences), sans pour autant détériorer
la capacité de filtrage en hautes fréquences.
Ainsi, d'après la figure 3.6, nous remarquons en effet
une atténuation rapide des oscillations comparativement à la
boucle ouverte, ce qui améliore aussi ses performances en temps de
réponse.
Le signal de commande est ajouté dans les figures de
réponses temporelles afin d'observer la force développée
par l'actionneur et son comportement.
3.6.2. Résultats de simulations LQG
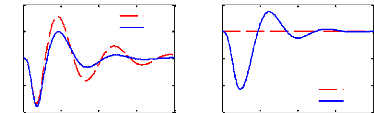
Les figures 3.7 et 3.8 montrent les réponses
fréquentielles et temporelles des critères.
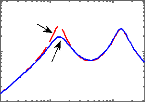
Diagrarwme de Bode du transfert Yacc(s)/w (s)
102
passif
101
actif
100
10-1
100 101
Magnitude (abs)
Diagranne de Bode du transfert Ypneu(s)/w (s)
1
passif
10-2
actif
10-3
100 101
Magnitude (abs)
10-
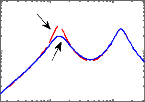
Frequence (Hz) Frequence (Hz)
100
Diagranne de Bode du transfert Ysusp(s)/w (s)
10-2
10-3
100 101
Magnitude (abs)
10-1
passif
actif
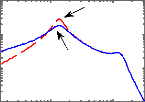
Frequence (Hz)
Figure 3.7 - Critères fréquentiels du
modèle quart de véhicule

53
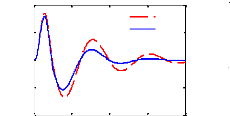
Amplitude (m/s2)
0.4
0.2
4
2
passif actif
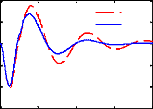
Accélération Verticale de Caisse
x 10-4 Ecrasement du pneu
-0.2
-0.4
0
Amplitude (m)
-2
-4
-6
0
|
Amplitude (N)
|
20
10
0 -10 -20
|
0 0.5 1 1.5 2
temps (s)
|
Amplitude (m)
|
4 2 0 -2 -4
|
x 10-3Débattement de suspension
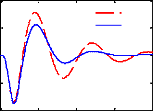
passif actif
0 0.5 1 1.5 2
temps (s)
0 0.5 1 1.5 2
temps (s)
Force de contrôle
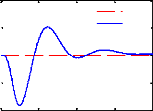
passif actif
0 0.5 1 1.5 2
temps(s)
passif actif

Figure 3.8 - Réponse temporelle du modèle quart
de véhicule avec le contrôleur LQG à
l'excitation ( )
Comparativement au cas passif, on constate que le
contrôle LQG permet aussi d'améliorer les critères
fréquentiels autour de la fréquence de résonance de la
masse suspendue ainsi que le temps d'atténuation des oscillations sans
pour autant détériorer la capacité de filtrage en hautes
fréquences. Cependant, il offre une marge de gain relativement
faible.
| 


