3.3.3. Structure de la de commande LQG
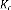
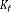
Le régulateur LQG qui réalise l'optimisation du
critère quadratique (3.8), est constitué de l'association d'un
retour d'état et d'un filtre de Kalman , soit :
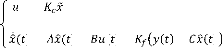
?
= -
) = ) + ( ) + - )
(3.9)
Où désigne le gain de l'observateur de Kalman,
calculé de telle sorte qu'il minimise la
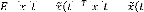
quantité : {[ ( ) - )] [ ( ) - )]}
Le gain du contrôle optimal et du filtre sont donnés
par:
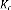
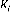
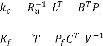
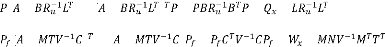
= ( + ) (3.10)
= ( + ) (3.11)

Où et sont solution des deux équations de Riccati
suivantes :
( - ) + ( - ) - + - = 0 (3.12)
( - ) + ( - ) - + - = 0 (3.13)

Avec = > 0 représentant la covariance de l'erreur
d'estimation - )
régime permanent.

41
Si l'état du système est entièrement
mesurable, le filtre de Kalman n'est pas nécessaire. On

obtient alors le régulateur en appliquant directement la
commande ( ) = - ( ).
Lorsque l'état du système n'est pas
entièrement mesurable, on implante la commande
par
l'intermédiaire d'un observateur. Le correcteur équivalent
( ) réalisant le rebouclage
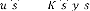
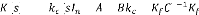
( ) = - ( ) ( ) est alors :
( ) = - ( - + + ) (3.14)
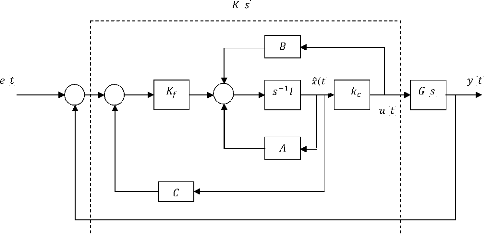
La structure de la commande LQG est illustrée par la
figure suivante :
( ) = 0
+ + +
+
-
+
+
( )
)
-
( )
( )
( )

Figure 3.3 - Structure d'un régulateur LQG
3.4. Commande LQG/LTR (Loop Transfert recovery) [13, 5]
La présence d'un observateur fait perdre les
propriétés de robustesse de la méthode LQR. Pour se
remédier a ce problème la synthèse d'une commande de type
LQG qui recouvre asymptotiquement soit les propriétés de
robustesse de la méthode LQ, soit celles du filtre de KALMAN est
nécessaire.
La méthode LTR (recouvrement du transfert de la boucle)
fait tendre asymptotiquement le transfert de boucle de la méthode LQG
afin de se rapprocher du transfert qui serait obtenu avec un réglage LQ
qui présente d'excellentes marges de stabilité.
3.4.1. Formulation du problème de commande
(LQG/LTR)
La méthode LTR ne concerne que les systèmes propres
définis par la représentation d'état ( , , , ) et qui
vérifie :
1' = 0 (strictement propre).
1' ( - ) à minimum de phase.
?

= (nombre égal d'entrées et de sorties).
3.4.1.1. Recouvrement en entrée

Cette première approche consiste à effectuer le
réglage des matrices et du filtre de

Kalman à partir d'un réglage nominale et en faisant
augmenter le paramètre du
nouveau réglage :
= +
, =
(3.15)
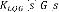
Afin que le transfert de boucle ( ) ( ) recouvre asymptotiquement
le transfert de
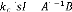

boucle - ( - ) de la méthode LQR.
uirn 8 ( ) ( ) = - ( - ) (3.16)
où
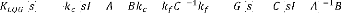
( ) = - ( - + + ) , ( ) = ( - ) (3.17)
3.4.1.2. Recouvrement en sortie
Cette seconde approche consiste à régler les
matrices et du retour d'état LQ à partir d'un

43

réglage nominale et en faisant augmenter le
paramètre du nouveau réglage :
= (3.18)
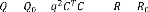
= +
,
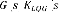

Afin que le transfert de boucle ( ) ( ) recouvre asymptotiquement
le transfert
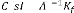
- ( - ) du filtre de Kalman.

uim
-*8
( ) ( ) = -- ( - ) (3.19)
| 


