3.5. Modèle du moteur dans le
référentiel de PARK :
Le principe consiste à convertir le système
triphasé précédent d'axes as, bs et
cs en un système diphasé d'axes d et q
équivalent. Compte tenu de la figure I-3.1, cette transformation aboutie
à la matrice de PARK [ P] :
(I-16) : [ P] =
1-
[
2
3
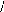
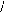
?
?
) ?
? ?
cose cos(9-- 2 7c 3 ) cos(9 -- 4 7c 3)

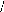
? sin ? ? sin( ? ?
? 2 3 ) sin(
? ? -- 4 7c 3
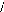
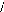
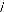
1 2 1 2 1 2
Matrice de PARK.
? ?
?
? ?
et sa matrice inverse :
(I-17) : [P]-1 =
cose --sin
i ?
?
? ?
0 1

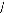
cos(9 -- 2 7c 3 ) --sin(9 -- 2 7c 3 ) 1
cos(9-- 4 7c
3 ) --sin(9 -- 4 7c 3 ) 1
Matrice inverse de PARK.
Avec la matrice [ P] , il est ainsi possible de
passer d'un système à l'autre. Pour cela, on utilise les
transformations suivantes :
? ? ? ?? ? ? ? ? ? ? ?
i ? P i ? i ? P i
? 1
dqo s abc s abc s dqo s
? ? ? ?? ? ? ? ? ? ? ?
1
v P v ? v ? P v
?
?
dqo abc s abc s dqo
s s
? ? ? ?? ? ? ? ? ? ? ?
? 1
? ? P ? ? ? ? P ?
dqo abc s abc s dqo
s s
(I-18)
L'unicité de la matrice de transformation [
P] pour les tensions, les courants et les flux, nous
oblige à tenir compte des changements de variables suivants :
2 2
? ds
3 3
i i
? ? v ? ? v ? ? ?
ds ds ds ds ds
2 2
i i
? ? v ? ? v ? ? ? ? ?
qs qs qs qs qs qs
3 3
1 1
i i
? ? v ? ? v ? ? ? ?
os os ds os ds os
3 3
(I-19)
Il faudra faire ATTENTION que dans tout ce qui suit,
nous utiliserons
des notations non primées pour simplifier les
écritures (Sauf indication
contraire).
? Pour retrouver des vraies valeurs de flux et de tensions sur
les axes d et q, il faudra multiplier chaque résultat par 3
2 (les résultats sur les courants restent identiques).
A partir d'un calcul que l'on ne démontre pas, on obtient
:
i
i
i
vds
ds
1 ?
?
? ?
?
qs
[Rs]
+0)
v qs
1 ?
?
? ?
r I
[
F I
[
r I
[
os
v os
|
F I
[
|
'Yds
Tqs
Tos
|
1 ?
?
? ?
|
+
|
d
dt
|
r I
[
|
tPds
Tqs
Tos
|
1 ?
?
? ?
|
0 --1 01
?
1 0 0 ?
0 0 0 ? ?
(I-20)
On en déduit les équations de PARK :
dlds
+ ?
dt
dlidt qs v qs = R s iqs + +
v os = R s i os
(Attention aux valeurs primées)
EQUATIONS DE
PARK DU MOTEUR DISCOIDE A
RELUCTANCE
VARIABLE ET A AIMANTS PERMANENTS ALTERNES.
v ds = R s ids
colliqs
Wt
ds
+ dIos
dt
(I-21)
On sait que ? ? abc ? s ? ? s ? abc ? s ? ? abc ?
aim
? L i ?
On multiplie chaque terme par la matrice de PARK, ce qui nous
donne :
? ? ? ? ?? ? ? ? ? ?? ?
? P L i ? P
dqo s s abc s ? abc aim
(I-22)
On remplace [ iabc] s par [ idqo?
s ? ? ? ? ? ?? ? ? ? ? ? ? ?? ?
? P L P i
?1 ? P
dqo s s ? abc aim
dqo s
Après un calcul, on obtient pour le premier terme :
?
? ?
i ? 0
dqo s ?
?
l ? 3 2 L 0 ? ?
i
f ms ? dqo
f ?
? ? ? ? ? ?
0 0
1
s
0 0
l ?

l f + 3 2 Lms

? ? ?
L M
? 0 0
p
?
? ?? ? ? ?
P L i
s . abc
s
? ? 0 ? ?
L M
? 0
p
? ? 0 0 ? ?
L ? 2 M ? p
.
1
Avec L p = l f #177;
Lms et M = -- 2 Lp
(I-23)
r ?
? ?
L

Et pour le second terme :
[P ][Tabc ]aim
? ? 0 0 ?
aim ?
0 0 0 ?
0 0 0 ? ?
(I-24)
Remarque
importante:
Transposé sur l'axe d, le flux
créé par les aimants (déterminé par un essai) doit
être
normalement majoré du coefficient 3/2 (unicité de
la matrice de Park). On aurait donc:
? ???daim = ?aim
?
? ? daim ? 3 ? ?
aim
2
Pt
Etant donné que nous utilisions des valeurs non
primées, on en fera de même pour 'gdaim
.... ....
? D'après la nouvelle notation, on a :
lidaim = Taim
1 ?
?
? ?
l f + 3 2 Lms
ds
i
i
i
0 0
1 ?
?
? ?
?
qs
0 l f +3 2 L 0
ms
? ? ds
?
?? qs ? ? 'Fos
0 0
r
[
r
[
lf
os
L'expression des flux dans PARK est :
? ? ? ? ?
daim
? ? ?
? 0
? ? ?
? ? ? ? 0 ? ?
(I-25)
(I-26)

?
? i ?
ds
? ?
?i qs ?? ? i ? os ?
?
? ? L i ? ?
ds d ds daim
? ?
avec ? daim ? aim
? et
3
L d ? L q ? L s ? l f ? L ms L o ? l
2 et
Attention aux valeurs primées.
f
? ? ?
ds
? ?
?? qs ?? ? ? ? os ?
d
? ?
0 L 0 ? q ?
? ? 0 0 L ?
o ?
? L 0 0 ?
1 ?? 0 ?
0 ? ?
? ?
?
? ?
.
?
? daim
?
? L i
qs q qs
? L i
os o os
?
?
Ld : Inductance synchrone d'axe direct
(longitudinale).
Lq : Inductance synchrone d'axe en
quadrature (transversale). Ls : Inductance
synchrone.
En remplaçant Ilids , Wqs ,Ios
par leur expression dans les relations (I-21), on obtient :
v ds = R s i ds +
Ld
-- co L q i qs +
difdaim
dt
di ds
dt
Avec
L d = Lq
Le flux 'km est constant par rapport
au temps = Le dernier terme de l'expressionprécédente
s'annule.
?
?
I
ds
di
?
w
dt
di qs
dt
di os
dt
v ds = R s i ds +
Ld
v qs = R s i qs + Lq
v os
= R s i os + Lo
L q iqs
#177; wL d ids #177; W taim
(I-27)
D'après cette remarque, les deux
derniers termes de v qs correspondent à des
f. e.m de
rotation puisqu'elles sont créées par la rotation
d'un flux qu'il soit variable ou non. On pose :
e qs = W ( L d i ds #177;
lifdaim ) et eds =
Lq0) i
qs
v ds = R s i ds +
Ld
v qs = R s i qs +
Lq
v R i L
? ?
os s os o

ds
di
?
eds
dt
qs
di
+
eqs
dt
dt
di
os
avec
e ds ? L q ? i qs et e qs ? ?
? L d i ds ? ?? daim ?
1daim = +aim
et
3
L d = L q = l f + L ms L
o ?
2 et
(Attention : Ce sont en réalité toutes des
valeurs primées)
lf
(I-28)
A partir de ces expressions, on peut schématiser le
système de la façon suivante :
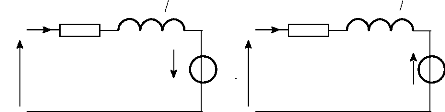
L d = l f + 3 2Lms
Lq = Ld = lf + 3
2Lms
i qs
vds
Rs
e qs = Ldco ids + CO
41 daim
ids
Rs
e ds = L q oiqs
v qs
ios Rs Lo =l
f
Fig. I-3.4 : Loi d'Ohm des circuits équivalents d'axes
d, q et o.
La puissance électrique instantanée, fournie par le
réseau et consommée par le moteur, est de la forme :
P e = v as i as + v bs i
bs + v cs ics
? En appliquant Park, on obtient la nouvelle expression :
|
3
P e = 2
|
( v ds i ds + v qs i qs + 2v
os i os )
|
Si on exprime la puissance en fonction des flux et des courants,
on obtient :
31-
e 2 L
P = IR s i ds 2 + ids
dtlj d ? d ?
1
I J
ds 2 qs 2 os
? i ? ? ? R i ? i ? i ? ? ? 2 R i ? 2 i
ds qs s qs qs qs ds s os os
dt dt dt
On organise chaque élément de l'expression pour
faire apparaître le terme correspondant à la puissance
électrique absorbée par le moteur et transformée en
puissance mécanique transmise à l'arbre du moteur (dernier
terme).
3 3 ? d ? d ? d ? ? 3
2 2 2 ds qs os
P ? R i
? ? i ? 2 i ? ? i dt i
? ? i ? ?
? i i ?
e s ds qs os ds qs os qs ds ds qs
?? 2 ?? ? ? ?
2 2 dt dt 2
On obtient ainsi :
3
? ?
T em ? Np iqs ds ? ids
qs
?? ? ?
??
2
(I-29)
L'expression peut se simplifier en remplaçant les flux par
leur expression. On obtient:
3
T em ? Np daim i qs
??
2
Il est très intéressant de constater que le
couple électromagnétique est directement
proportionnel au
courant i qs . On se retrouve donc dans les
mêmes conditions que le
moteur à courant continu.
Tem = Tq = KT iqs
avec
·
·
p'I`daim en N.m/A : Constante de
coupleet
Td = 0
3
K = 2N
T
(I-30)
| 


