Chapitre 1 : Présentation et Modélisation
du prototype - Mémoire CNAM Patrick BOIDIN.
.
?
90°
-->
Vs
cot
90 + cot
er
0
-->
co L s I s
cot + o s 0
as (Fixe)
(1)
?
?
Es
8
-->
IP aim
cot
?
-->
cot
Is
cot
9
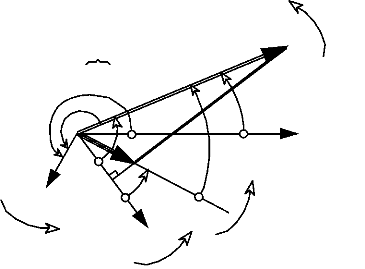
Fig.I-3.3 : Diagramme vectoriel dans l'hypothèse de
Behn-Eschenburg.
On n'a pas représenté la chute de tension
résistive.
3.3. Problème lié à la
résolution des équations dans le repère (as,bs,cs) :
Si on remplace l'expression des flux dans les relations (I-2), on
obtient :
? v ? R ? i ? ? L ? d ? ? ? ? ? ?
d
? ? dt i ? ?
abc s s abc s s abc s abc aim
dt
(I-10)
Sachant que :
?
? ? abc ? aim ? aim
? ?
? ?
? ?
cos(cot + 90)
?
cos( ? t ? 2 3
? ?
? 0 ) ?
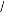
cos( ? t ? 4 3
? ?
? ) ? ?
0
on en déduit :
sin(wt + 90)
?
sin(wt - 2 7c 3+90 ) ?
sin(wt - 4 7c 3+90
?
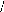
?
: fonction du temps.

[Tabc]
=- cotlfaim
d
dt

aim
? ?
?
? ?
On reprend l'expression (I-10) pour la mettre sous la forme d'une
représentation d'état d'un système d'équations
différentielles que l'on connaît. On obtient :
sin (o)t+ 90) (wt-2 7c 3+90) (cot-4 7c 3+90)
? ?#177;R s [L ]--
s 1 [iabc ]s =[ns
1[vabc ]s
#177;(134faim [L]
1
?
?
? ?
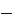
d
dt
? 1
s
? ?
?
? ?
sin sin
(I-11)
? [ ( ) ] [ ] [ ( ) ] [ ( ) ] [ ( ) ]
dt X t + A X t = B t + C t
En supposant que la vitesse reste constante durant la
variation des courants (critère de linéarité), on a alors
un système différentiel linéaire du 1er ordre à
coefficients constants, au premier membre (en fonction du temps) et au second
membre, variable dans le temps. La solution particulière de ce
système est obtenue par la méthode de variation des constantes.
Cette méthode de résolution est coûteuse en temps et en
moyen de calcul (système à 3 équations). L'utilisation du
formalisme de Park contribuera peutêtre à améliorer la
résolution de ce système et simplifier la commande.
3.4. Equations mécaniques :
L'expression du couple électromagnétique, pour un
moteur multipolaire, est de la forme:
|
3
Tem = N p
2
|
?i i j - j i ?? ?i
|
(I-12)
Np correspond au nombre de pas du
moteur discoïde. L'équation du mouvement est de la forme :
d ?
) dt
T T J J em - r = ( m +r
(I-13)
?
Sachant que L = , on a :
Np
1
dw 1
dt ??
r
T T
( m + r )
? = N J J
p
em r ??
(I-14)
On peut émettre une remarque importante sur la
représentation physique du couple
résistant . En effet, ce
couple représente en réalité la somme de 3 couples qui
Tr
s'opposent à la rotation du moteur. Ils sont :
· Un couple résistant, dû aux frottements
visqueux que l'on notera Trf. Ces frottements sont
proportionnels à la vitesse et sont provoqués par les roulements
à billes, la circulation de l'air dans l'entrefer et le ventilateur de
refroidissement du moteur (absent dans notre cas). On a: Trf
= fw.
· Un couple résistant résiduel dû
essentiellement aux aimants dont les lignes de champs se referment selon la
règle du flux maximal et tendent à s'opposer à la rotation
du moteur. Ce couple est indépendant de la vitesse, on le notera
Tr0.
· Un couple résistant, dû à la
machine entraînée que l'on notera Trma.
On obtient ainsi une nouvelle expression :
1 ?
? N J
(
?? m ?
p
T em -- (Trma + T r f #177; T r 0 )
Avec
T rf = f co
te
T r0 = Cte
T rma = k o)2 ou k o)3 ou k a ou
Cs
(I-15)
| 


