3. MODELISATION DU PROTOTYPE.
Le moteur, tel que nous l'avons observé, s'apparente
à une machine synchrone à aimants permanents. On utilisera donc
les équations électriques et magnétiques de cette machine.
L'élaboration d'une commande efficace et dynamique de type
"vectoriel", nécessite d'utiliser le formalisme de Park. C'est
pourquoi, nous définirons notre système dans le
référentiel (d,q) de Park.
3.1. Conventions et hypothèses :
On suppose que la machine étudiée, répond
aux conditions d'étude suivantes :
· Enroulement multipolaire.
· Absence de saturation dans le circuit
magnétique.
· Absence d'effet pelliculaire.
· f.m.m. supposée sinusoïdale. On ne
considère que le premier harmonique d'espace de la distribution de
f.m.m.
· Le rotor tourne positivement dans le sens
trigonométrique.
· Par convention, l'induit (stator) est
considéré comme un récepteur.
· Le rotor est à pôles lisses et à
entrefer constant.
· On néglige les amortisseurs.
· L'axe Oq est en avance sur l'axe Od.
· Un courant positif génère un flux
positif.
· Une f.e.m. positive fait circuler un courant positif.
· On néglige les pertes magnétiques.
· Le flux inducteur, créé par les aimants,
est aligné suivant l'axe du rotor.
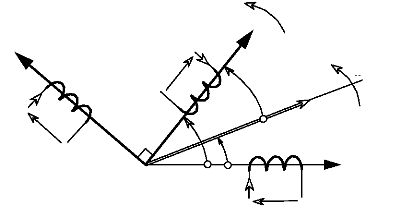
La construction vectorielle, telle que nous la présentons
par la figure I-3.1, est très importante et servira de base à
toute l'étude sur le moteur.
d
7
ids
q
iqs
vds
Axe
du
rotor
(0
(Fixe)
as
(0
ias
-->
? aim
vqs
O
a + a 0
? ? ? 0
vas
Fig.I-3.1 : Construction vectorielle avec l'axe d non
aligné avec l'axe du rotor.
Pour t=0 = a = et 0 = .
L'angle y correspond au décalage entre l'axe d et l'axe
du
0 0
rotor. Nous verrons, par la suite, qu'il faut caler ces 2 axes
entre-eux de façon à obtenir
7 = 0 soit
a = 0 . Ainsi, la matrice de Park fera intervenir uniquement
l'angle 0. Il est
important de préciser que les 2 enroulements
représentés sur les axes d et q, sont purement fictifs. Les
grandeurs engendrées par ces enroulements, seront créées
et évolueront par l'intermédiaire d'un algorithme
numérique. La position initiale du rotor est l'élément
indispensable au bon fonctionnement d'une commande vectorielle et nous verrons
pourquoi, par la suite.
L'angle 0 correspond à la position du
rotor par rapport à l'axe fixe de la phase a
s.
3.2. Mise en équations du moteur à
l'étude dans le repère (as,bs,cs) [4] [5] [6]:
· La loi d'Ohm avec la convention récepteur du
circuit d'induit, s'écrit :
dP is
dt
v is =R s iis +
(I-1)
Rs
d'is
dt
+
d'Pas
dt
iis
Fig. I-3.2
L'inducteur est représenté vectoriellement par son
vecteur flux, d'amplitude supposée constante :
?
IP aim
Appliquée aux phases statoriques as,
bs, cs du moteur, on obtient les expressions :
v as = R s ias
?#177;
(Nibs 1 as
dt
cs
r
1
r
1
v bs = R s ibs
[
v
v
v
bs
1
L
i
i
i
d
dt
gi
bs
Wcs
T
1
as
[
I I
I
J
Rs
I =
J
bs
I+ J
cs
+
dIcs
dt
v cs = R s ics
Sous une forme matricielle, on a :
1
[ v abc ] s = R s [i abc is #177; dt [Tabc
j1
s
(I-2)
· Suivant l'hypothèse de base, c'est à dire,
le circuit magnétique non saturé, on peut lier les flux et les
courants par les relations suivantes :
Was = L pa i as + M ab
i bs + M ac ics + Wa aim Tbs = M ba i as + L
pb i bs + M bc ics + gib aim
Wcs = M ca i as + M cb i bs + L pc
ics +'Pc aim
Avec :
1
3 + 00
tpa aim .tPaim cos(COt +
90)
cos(o)t--
cos(o)t--
2 7c 3+90)
4 7c 3+90)
?
Tb aim = Taim
?
NIc aim =
tilaim
(I-3)
D'après la forme et la constitution du rotor que nous
avons décrit précédemment, il est possible de
considérer la machine comme étant à pôles lisses et
à entrefer constant. On peut écrire :
· L pa = L pb = L pc = Lp :
constante (valeur qui ne dépend pas de la position du
rotor).
· M ab = Mbc = Mac = M:
Mutuelle à valeur constante valeur qui ne dépend pas de
la position du rotor.
En tenant compte de cette précision, on peut mettre les
relations précédentes sous la forme matricielle suivante :

? ? cos ? ?
? ?
aim 0
as
i
i
i
?
1 ?
?
? ?
+
Taim
r 1
[
bs
i ?
?
? ?
?
r
[
Taim
cos(O t -- 4 7C 3 + 90
1
?
?
? ?
cs
Tas
F
1
?? bs ? ? tics
r ? ?
L
p
t ? ?
?
cos( ? t ? 2 3
? ?
? 0 ) ?
? ?
L p M M
M L p M
M M L
(I-4)
Sachant que :
L p = l f + Lms et
M = -- 12 Lms
·
·
Taim
?
Taim
i
i
i
as
1 ?
?
? ?
+
bs
r
[
r ? ?
L
cs
L'expression (I-4) devient :
rl f #177; Lms _ 1 2 L ms -- 1 2
Lms
? ?
? ? 1 2 L l L
? ? 1 2 L
? ms f ms ms ?
? ? ? 1 2 L ? 1 2 L l L
? ? ?
ms ms f ms
(I-5)
En l'absence d'un fil neutre relié à la terre, on
a:
? ? cos( ? ?
t ? ?
aim 0 )
?
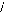
cos( ? t ? 4 3
? ?
? 0 ) ?
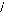
cos( ? t ? 2 3
? ?
? ? ?
0 )
i as + i bs + i cs = 0 ?i bs + i cs =
--ias
Ce qui nous donne :
I
? 3 ? di as
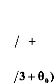
0
9
2
273 3
e0)o)
47c
v R i
? ? ?
l L ? t
as s as f ms aim
?? ?? ? ? sin(
? ? ?
2 dt
? 3 ? di bs
v R i
? ? ?
?? l L ? ? ? t ?
bs s bs f ms ?? ? ? sin(
aim
2 dt
? 3 ? di cs
v R i
? ? ?
l L ? t
cs s cs f ms aim
?? ?
?? ? ? sin( ? ?
2 dt
(I-6)
En reprenant les relations (I-5) et en posant :


1 ?
? ? ? : Matrice des inductances statoriques.
ms
ms
l f + Lms -- 1 2 L ms -- 1
2L
1 2 L ms l f + Lms -- 1
2L


1 2 L ? 1 2 L l L
?
ms ms f ms
et
?
? ? abc ? aim ? aim
? ?
? ?
? ?
cos(cot + 00)
?
: Matrice des flux de l'inducteur.
cos( ? t ? 2 3
? ?
? 0 ) ?

cos( ? t ? 4 3
? ?
? ) ? ?
0
On obtient une forme matricielle :
[IF abc ? s ? ? s ? abc ? s ? ? abc ?
aim
? L i ?
(I-7)
On sait que :
?
d tP a
aim
e as
_ --
dt
liPaim
d cos(wt+ 90 ) d cos(cot +
90)
? ? ? ? as ? ? aim
e ? ? ? sin ? ?
? t ? ? 0
aim
dt dt
En raisonnant de la même façon pour e
bs et e cs, on obtient les
équations suivantes :
v as = R s i as +
Ls
v bs = R s i bs +
Ls
v cs = R s i cs +
Ls
I
1
?
L

as
di
as
bs
di
bs
di
cs
?
ecs
dt
Avec
3
e as = ct?
aim sin(cot+ 00)
e bs = Chaim sin(cot -- 2i 3+ 0 0
)
·
·

|
e cs = claim sin(cot -- 47c
|
|
3 + 00)
|
E ? ? ?? ?
aim
(I-8)
Soit en notation complexe:
Vs= R s I s +
jcoLs I s -- j OFaim
ou
Vs =RsIs +
jco(Ls Is --Taim)

(I-9)
On représente les relations précédentes sous
la forme vectorielle suivante :
| 


