Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

3.6. Remarque sur la transformation de Park et du système résultant :

Mise sous une autre forme et tenant compte que L _q = L_d , la transformation de Park permet d'obtenir les relations très importantes suivantes :

di ds

dt

qs

R 1

? L ⁱ _L v

s ? ? ? i

ds ds

d d

di

qs

dt

ce

? daim

R 1 1

+ ^s i qs = vqs --co i ds -- L d

L d L d

e ds =
e qs =

(L qs d i

?L i ? ? ? ? d ds daim

co

ce

?

? ? ?

3

T ? N ? i

em p daim qs

2 avec ^tlⁱdaim =aim

ce

dw

dt ?

f N p

J _m +Jr

N_p

? J _m +Jr

(K _T i -- T r 0 -- Trma)

(I-31) Attention : Ce sont en réalité des valeurs primées.

? Sous une forme matricielle, on a :

d R

? ? ? ? ? ?

1

s

dt i ?

dq s L i ?

dq s L v dq

d

d

? i ?

qs

? ?

??

? ?

i ?? ??

ds daim

s

(I-32)
On remarque que les courants de Park sont liés entre eux par la vitesse angulaire du
rotor Co. Le couple électromagnétique étant indépendant du courant i_ds, on peut

imaginer une loi de commande qui puisse maintenir ce courant nul. On aurait ainsi le courant i _qs qui crée le couple, découplé du courant i_ds qui crée le flux.

Remarques:

· En régime permanent, co = o s ? Le système d'axes (d,q) tourne à la vitesse de synchronisme. Toutes les grandeurs dans Park deviennent des constantes.

· L'annulation du courant _ids proposée précédemment, revient en définitive à

? ?

maintenir le vecteur -- E_s colinéaire avec le vecteur courant I s . Dans certain ouvrage, on dénomme cette commande par : « Commande à flux croisés ».

· Lorsque l'on aura besoin de déterminer vectoriellement les courants _ids et i_qs, il

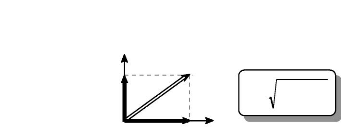
sur les axes d et q.

?

suffira de projeter le vecteur I_s

q

--)

I _s

"I_s =

( ?

i ds ? i qs

2 2

d

·

-->

-->

i qs

ids

Fig. I-3.5

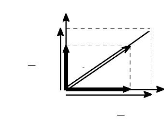
· On pourra effectuer les mêmes projections du vecteur flux et du vecteur tension à condition de tenir compte du coefficient 2 3 qui nous a permis d'unifier la matrice de Park. On rappelle que vds, vqs, vos, ^Wds, _tqset 'F_os sont en réalité des valeurs primées. Pour revenir aux vraies valeurs représentatives des axes a_s, b_s et c_s, il faut

3

multiplier les valeurs obtenues par 2 . D'une autre façon, on pourra augmenter de ce

même coefficient le module des vecteurs uniques avant de les projeter sur les axes d et q.

3

-->

-->

-³ 3 -->

v = vi

^qs 2 ^qs

--)

V_s

-->

vds

?

q

,

vqs

?

v _ds ? ?

v ds

2

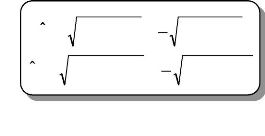
V

=

s

( v'ds 2 + v'qs² ) = 2 3 (+)

T_s

d

= ( ? s ? ? ? qs ? ? ? ? ds ? ? qs ?

₂ 2 2

? d 2 2

3

Fig. I-3.6

Cette partie d'étude nous donne 2 systèmes de représentation différente ; Le premier (I-11) dans le repère (a_s,b_s,c_s) et le second (I-32), dans le repère (d,q).

Or, dans les 2 cas, les équations différentielles sont à coefficients constants avec les hypothèses de bases. = Le changement de repère ne se justifie donc pas.

Dans les 2 cas, le second membre des 2 systèmes correspond à des fonctions variables en fonction du temps. On se retrouve donc avec le même type de problème. Par contre, quel que soit le régime de fonctionnement (transitoire ou permanent), le second membre du 1^er cas varie toujours en fonction du temps. Dans le 2^ème cas et en régime permanent, le second membre est constant. = Le changement de repère se justifie. Le nombre d'équations électriques, dans le système de Park, est limité à 2 pour 3, dans l'autre cas. ? Le changement de repère se justifie.