Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

· Le moteur a besoin d'une commande en M.L.I pour limiter au mieux les harmoniques de courants et surtout les à-coups de couple. Les moyens en informatique, à notre disposition, ne permettent pas d'utiliser une M.L.I à une fréquence plus élevée que celle utilisée de 2,4 khz. Compte tenu des bons résultats obtenus, on peut s'imaginer que les résultats seraient bien meilleurs à des fréquences supérieures.

· La remarque précédente nous motive à écarter la solution du contrôle des courants par "hystérésis". En effet, cette méthode ne permet pas de contrôler suffisamment bien les harmoniques de courant, pour favoriser son emploi.

· Qu'elle que soit la position initiale du rotor, imposée avant chaque démarrage, le comportement du moteur n'a pas varié.

· Muni d'un découpleur linéarisant, le moteur discoïde et sa commande deviennent assimilables à un moteur à courant continu. L'inconvénient principal de ce découpleur réside dans l'estimation de la valeur numérique des paramètres du moteur. En supposant que ces paramètres évoluent en fonction des données tel que la température ou autres, il faudra réajuster les valeurs en conséquence. Cette condition impose de bien connaître les caractéristiques électriques du moteur considéré ou d'intégrer dans la commande du moteur des opérations de mesures des paramètres électriques.

· Le moteur a besoin d'être régulé avec beaucoup de souplesse pour des fonctionnements dont le couple résistant est faible. En effet, si les paramètres des correcteurs optimisent les fonctionnements à fortes charges, le moteur aura tendance à pomper en dépensant inutilement de l'énergie sous forme de pertes magnétiques aux faibles charges. Dans cette situation, on devra adapter les paramètres des correcteurs au cas de fonctionnement donné. On appelle cette commande,

Commande adaptative.

En conclusion, la commande vectorielle s'adapte assez bien au moteur FINTRONIC, à condition de connaître à chaque instant, la position du rotor. La structure de cette commande est simple à élaborer, comparée à celle d'une commande vectorielle de machine asynchrone. Néanmoins et sans pouvoir le démontrer dans ce mémoire, le moteur perd très vite ses performances, à des vitesses supérieures au nominal. Une étude est nécessaire pour ce cas de fonctionnement.

CHAPITRE 4

COMMANDE SANS CAPTEUR
MECANIQUE DU MOTEUR FINTRONIC
ET
FILTRE DE KALMAN

1. INTRODUCTION.

Dans cette partie d'étude, on défini une commande sans capteur mécanique du moteur FINTRONIC. Cette commande est testée par une série de simulations sous MATLABSIMULINK dont on présente les résultats. Le chapitre précédent nous a montré que le capteur de position et de vitesse était indispensable à la fonction d'autopilotage et à la régulation de vitesse. Or, les difficultés rencontrées pour définir le capteur standard et compatible avec le prototype, nous conduit à étudier un moyen technique de substitution. Pour cela, on utilise un algorithme de contrôle-commande du type :

filtre de Kalman.

2. LE CAPTEUR DE POSITION. 2.1. Le capteur et son rôle :

Le capteur mécanique que nous proposons de définir avant de le remplacer, doit détecter la position angulaire du rotor par rapport à un repère fixe du moteur. On rappelle que le rotor est soumis à une fréquence de rotation nominale de 60 tr/min pour une fréquence électrique de 64Hz.

2.2. Résolution du capteur :

Le nombre de pas du moteur est de 64. Cela signifie que pour 1 tour mécanique du rotor, le champ statorique a fait 64 tours électriques. En imposant un pas de mesure de 1 degré électrique (1pt/°) qui correspond à une précision de 60'(minutes) et 360 pts sur le tour électrique, il faudrait une résolution de 23 040 points de mesure par tour mécanique (64x360) pour assurer le fonctionnement correct du moteur.

5,625° méca. 360° méca.

1 tour électrique 64 tours électriques

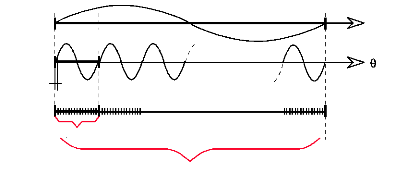
1 tour mécanique

0

⁹mec

360° élec.

1pt/° élec.

360pts

360x64= 23 040pts

Fig.IV-2.1

Or, le traitement des informations du capteur doit nécessairement se faire sur 15 bits au minimum (2¹⁵=32 768 pts).

2.3. Choix du type de capteur :

Il est possible de choisir parmi l'une de ces 3 catégories de capteurs "standard":

1. Le capteur de position angulaire du type codeur rotatif incrémental : La position angulaire est définie par un nombre d'impulsions sur le tour mécanique.

2. Le capteur de position angulaire du type codeur rotatif absolu : La position angulaire est définie par un mot binaire de x bits dans le tour absolu.

3. Le capteur de position angulaire de type résolveur : La position angulaire est fournie par 2 signaux analogiques (en cosinus et en sinus), porteurs de l'information de position. Un traitement du signal est nécessaire pour ce type de capteurs.

2.4. Le codeur rotatif incrémental :

Les plages de résolutions les plus courantes, proposées par les fournisseurs, sont comprises entre 50 et 10 0000 points par tour mécanique. Au-delà de 5 000 pts, le capteur devient sophistiqué et coûteux. Le principal inconvénient de ce capteur est de fournir une position relative par rapport à un point de référence "Top 0" qui se situe dans le tour mécanique. Tant que ce "Top 0" n'est pas sollicité, le moteur est commandé de façon aléatoire. Or, cette phase transitoire est d'autant plus longue que le nombre de paires de pôles du moteur est grand. Dans notre cas, cette phase peut durer prés d'une seconde (60 tr/min. = 1 tr/s). Evidemment, Cet inconvénient n'est pas tolérable pour une commande performante du moteur FINTRONIC.

2.5. Le codeur rotatif absolu :

Ce type de capteurs est proposé avec une résolution maximale et courante de 4 096 pts/tour mécanique ; C'est un codeur à 12 bits. Au-delà de cette résolution, le prix du capeur devient injustifié pour des projets comme le notre. En exemple, on peut citer HEIDENHAIN qui propose des capteurs 15 bits (32 768 pts/tour) pour un montant H.T. de 8 000 francs, l'unité. Ce matériel est aussi cher que le variateur de vitesse, lui-même. De plus, les informations doivent être traitées non plus sur 12 bits mais sur 16 bits. Par contre, le codeur absolu supprime l'inconvénient du cas précédent : L'autopilotage du moteur peut se faire instantanément sans phase d'incertitude et la position angulaire du rotor est déterminée dans le tour absolu.

2.6. Le résolveur :

Le résolveur est un capteur électromagnétique qui a l'avantage d'être dépourvu de toute électronique embarquée. Par sa constitution et par sa construction, il s'apparente fortement à un moteur synchrone dont on a mis en quadrature, deux phases statoriques. L'inducteur est alimenté par une tension alternative soumise à une fréquence maximale de 10kHz. On retrouve le principe du résolveur à travers cette figure :

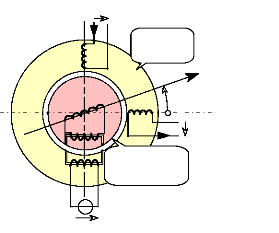
vs1

Signal de sortie
capteur

Partie fixe
solidaire du bati
moteur

Axe en rotation

Stator

Rotor

°mé c

Axe fixe de référence

vs2

Signal de sortie
capteur

Partie mobile
reliée mécaniquement
au rotor du moteur

V e ( 10kHz)

Signal d' entrée

Fig.IV-2.2 : Capteur de position type "Résolveur".

L'amplitude des tensions de sorties de ce capteur varie en fonction de la position du rotor. La modulation de ces amplitudes permet de déterminer la position du rotor par rapport à un axe de référence du résolveur. La fréquence de la modulatrice permet d'obtenir la fréquence de rotation du moteur tandis que la fréquence de la tension d'entrée, donne la résolution. Elle correspond à 10000 50 variations pour 3 000

tr/min, soit 200 pts par tour mécanique. On peut atteindre 5 000 pts/tour mécanique en ajoutant au dispositif, un module électronique dit "de positionnement".

L'inconvénient principal de ce capteur est de fournir une mauvaise précision de la mesure aux basses vitesses.

En préliminaire, on constate que les capteurs proposés ne conviennent pas tout à fait au prototype : La résolution de 4 096 pts/tour n'est pas suffisante comparée aux 23 040 pts/tour recherchés. Néanmoins, une solution consisterait à augmenter le rapport des vitesses en interposant entre le moteur et le capteur, un train d'engrenages.

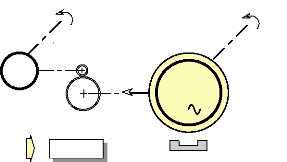
Train d'engrenages
R=4

Codeur
12bits

MS

3

Aimants P.

4 tours mécaniques

1 tour mécanique

1,41°/pts

Fig.IV-2.3 : Capteur de position avec train d'engrenages.

2.7. Conclusion :

Pour installer un capteur de position sur le prototype, il faut un codeur rotatif absolu à 12 bits (- 4 000 francs.) mais sans son train d'engrenages. En effet, ce dispositif augmente la résolution du capteur mais augmente aussi sa sensibilité face aux imperfections du train d'engrenages (jeux) et aux vibrations mécaniques parasites du moteur. La solution sans engrenage permet de filtrer naturellement la mesure de la position qui est détectable à environ #177; 3° de l'angle électrique. Cette solution s'oppose, néanmoins, à une commande optimale.

3. RECONSTRUCTION DE LA POSITION DU ROTOR AU MOYEN DU RECONSTRUCTEUR D'ETAT.

3.1. Le reconstructeur et son principe, appliqués aux systèmes linéaires :

Un reconstructeur d'états [13][14] est un dispositif capable d'estimer une ou des grandeurs d'états non mesurables d'un système, à partir des grandeurs mesurables dites observables. Cette définition fait apparaître la notion d'estimation. Le problème essentiel d'une valeur estimée est de pouvoir juger son degré de fiabilité. Pour cela, on se sert d'une autre grandeur du système qui est estimable et mesurable pour corriger les estimations des grandeurs non mesurables à travers des gains de correction.

Un reconstructeur d'états est donc un estimateur à la fois correcteur des variables d'états. On schématise le principe par le schéma suivant :

Réseau

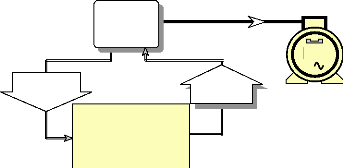
Cde

MS

3

Grandeurs
mesurables

Grandeurs
estimées

Reconstructeur

Estimation
+
Correction de l'erreur

Fig.IV-3.1 : Principe du reconstructeur.

L'idée du reconstructeur consiste à reconstruire l'ensemble des variables d'état du
moteur contenant les grandeurs non mesurables. On le fait partiellement ou en

totalité. A partir de la représentation du moteur par le modèle d'état, on schématise le principe du reconstructeur d'états dans sa phase estimation [15]:

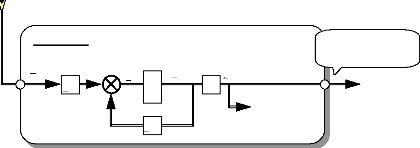
u( t ) i( 1(t)

+

Estimateur

g ? t ?

+

f ?t)

?

C

y? ( t)

Variables de sortie
estimées à
valeurs observables
sur le processus

Variables de sortie
de l'estimateur à
valeurs non-observables
estimées

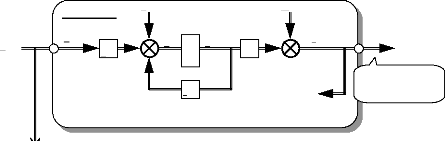
u( t)

Processus

u( t)

g ? t ?

+

v(t)

+

+

x? ( t )

f ?t)

J^.

x(t)

Variables de sortie
du processus à
valeurs non observables

C

+

w( t)

+

y(t)

Variables de sortie
du processus à
valeurs observables

Fig. IV-3.2 : Le processus et son estimateur fonctionnant en parallèle.

Nota :

· La moins mauvaise estimation d'un bruit, agissant sur un système, consiste à la supposer nulle. C'est pourquoi les vecteurs "bruits" v( t) et w( t) du système à variables estimées, n'apparaissent pas dans l'estimateur.

· u (t ) correspond au vecteur d'entrée du système dont les variables sont fonctions du temps. Les variables peuvent être les tensions ou les courants.

· y (t ) et x (t )correspondent au vecteur de sortie et au vecteur d'état du système dont les variables sont fonctions du temps. Ces variables peuvent être les tensions, les courants, la position et /ou la vitesse angulaire.

Le moteur et l'estimateur obéissent aux 2 systèmes différentiels suivants :

d dtx t f t x t g t u t v t ? ? ? ? ? ? ? ? ? ? ? ? ? ? + y t C x t w t ? ? ? ? ? ? ? +	et	d dt = 71( + y t C x t ? ? ? ? ? = ?

(IV-1) : Processus et estimateur.

Nota :

La matrice C est considérée à coefficients constants.

Or, dans cette configuration, rien ne nous permet de vérifier si les valeurs estimées sont fiables ou non. Il faut rajouter un dispositif de vérification et de correction des variables d'états estimées :

u( t)

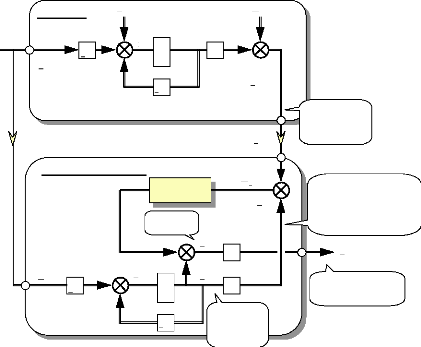
Processus

u( t) + i( t) 1( t)

u( t)

Reconstructeur d'états

g( t)

g( t)

+

v( t)

+

+

+

x? ( t )

K
Gain de Correction

Nouvelle
estimation

f( t)

f( t)

I

I

+

x( t)

+

x? _c ( t)

C

Ancienne
estimation

C

C

y( t)

E _y ( t)

y? ( t)

+

y( t)

w( t)

+

+

-

Variables de sortie
du processus A
valeurs observables

Variables de sortie
de l'estimateur A
valeurs estimées non corrigées
observables
sur le processus

Variables de sortie
de l'estimateur A
valeurs non-observables
estimées et corrigées

3%_c( t)

Fig.IV-3.3 : Processus avec son reconstructeur d'états.

Reconstructeur d'état :

d

_dt i^sk( t ) = f ( t ) l4 t ) + g ( t ) u ( t) A t ) = C ii( t)

(IV-2)
Vérification de l'erreur sur la sortie :

E_y ( t ) = y( t ) -- y? ( t)

(IV-3)
Correction de l'estimation du vecteur d'état :

?x _c ( t ) = ?x( t ) + K E _y ( t) ? Nouvelle estimation.

(IV-4)

Le principal inconvénient de cette méthode est de conserver constant dans le temps, les coefficients de la matrice de gains de correction. Il faut nécessairement optimiser la valeur de ces coefficients, quel que soit le fonctionnement du moteur.

De plus, la mesure des grandeurs observables doit être la plus précise possible pour permettre une comparaison efficace sur les sorties et permettre une commande toute aussi efficace de l'estimateur. Il est important de préciser qu'un reconstructeur d'état fait appel à des moyens de calculs sophistiqués dont les temps de calculs dépendent essentiellement de l'ordre du système = D'où l'utilisation d'un microcontrôleur spécifique, propre à cette fonction. Le traitement de l'information, au moyen d'un pC, impose que le système continu soit converti en un système discret. On obtient ainsi une nouvelle représentation du système différentiel. Pour cela, on pose :

x? tk) = x_k , avec k correspondant au pas d'échantillonnage à l'instant tk. On obtient [13] :

k k

e g ? ? u ? ? ? d ? e

f k

( , )

? f k

( , )

?

? ? ? ? ? v(T)) dT

k-1 k-1

? 1

x _k e f k k

( , ) ?

? x ?

?

k 1

?

(IV-5)

Le 1^er terme de l'expression (IV-5) correspond à la solution générale du système différentiel sans second membre.

_ef ( k , k- 1 ) correspond à la matrice de transition du système (passage de x_k_₁ à x_k). On notera ce vecteur :

f k k

( , )

? f k

( , )

?

? ? k ,k ?1 ? ? ? ? k k ? e

, ? 1 ? ¹ et ? ? k ?

, e

?

?

(IV-6)

Le 2ème terme du second membre de l'expression (IV-5) correspond à la solution particulière du système différentielle avec second membre tenant compte de la condition initiale. Durant la période comprise entre les 2 pas d'échantillonnage k et k-1, on peut considérer que u(ti) est resté constant. D'où :

k ? k ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? g u d ? ? ? ? ? ? ? k g ? ? k , ? , k ? 1 ? k-1		1 d u k g d k u k ? ? ? ? 1 ( ) ? ? 1 1 ?
(IV-7) Le 3^ème terme du second membre est mis sous la forme : k v d k ? ? ? v ? ? ? 1 ? ? ? ? ? ( ? ) k , k-1	dr

(IV-8)

Le système différentiel, représentant le processus et le reconstructeur, devient sous la forme d'un système discret suivant :

Processus (moteur + machine) :

1. Estimation sous forme de prédiction :

2. Mesure des grandeurs de sortie mesurables et comparaison :

(IV-11) : Cy ? k) ? y ? y --

?

k k k

/ 1

3. Réajustement des estimations :

X k k X k k K y _k y k k

? = ? ( ? )

+

/ / ? 1 / _ 1

et

y / C X /

? k k = ? k k

(IV-12)

X = I , _ X + g u

k ( )

k k 1 k _ 1 d k

? ?

? 1

y C X w

= +

k k k

Reconstructeur d'état

(IV-9) :

:

X + g

( )

k k

, -- 1 k k

? ?

1 1

/ d k

? ?

? 1

y ? = C X ? k k

/ ? 1

k k

/ -- 1

(IV-10) :

X ? _ I ?

k k

/ ? 1

u k --1

+ v

k -- 1 d k

(

- 1)

Nota:

Pour éviter des confusions, nous avons rajouté volontairement un terme supplémentaire en indice à chacune des variables discrètes ? X k/ k (2ème k). En effet, ce terme correspond au pas d'échantillonnage pour lequel on a réalisé les mesures. Ceci nous permet de savoir si l'estimation est réalisée avant ou après la mesure.

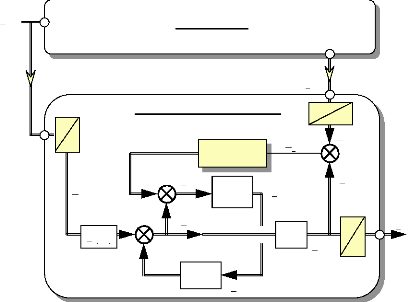
u( t)

t

k

uk?1

gd k_1

( )

+

Reconstructeur d'état discrêt

+

+

+

Processus

? X k/ k

? X k/ k? 1

? ( k , k-1)

K
Gain de Correction

Retard

? X k ? 1 / k ? 1

? X k ? 1 / k ? 1

y_k

+

? y( k)

C

y( t)

y k k- 1
/

?

t k

-

?

y k k- 1
/

k

t

y? ( t)

Fig.IV-3.4 : Reconstructeur discret.

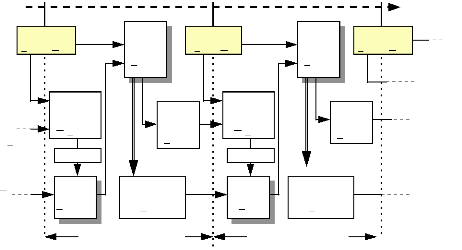
Pour mieux comprendre le rôle du reconstructeur, on detaille de façon chronologique et sous forme de schema, les differentes tâches a realiser par le 1.1C.

¹¹¹(k,k-1)

O( k +1,k9

tk-1 Matrice de transition t_k Matrice de transition tk+1

...

x k - 1 /k-2

y

k- 1 /k-2

Mesures de yk-1 et uk-1

Détermination
de
l'erreur

⁶ y ( k- 1)

Estimation
de

x ? k- 1 /k - 1

Correction

Tâches à réalisées
par le microcontrôleur
dans l'intervalle de temps

Mise en mémoire
de

Estimation
de

? x k/ k-1

x k/ k-1

?

Estimation
de

yk /k-1

Mesures de y_k et uk

Détermination
de
l'erreur

C y(k)

Estimation
de

x ? k / k

Correction

Tâches à réalisées
par le microcontrôleur
dans l'intervalle de temps

Mise en mémoire
de

Estimation
de

? x k+1/k

x k+1/k

?

Estimation
de

,,

yk+1/k

Mesures de yk+1 et u _k+1

Temps en P s

t k -1, t k t k , t k +1

Instant oil les données sont

saisies par le
microcontrôleur

Fig. IV-3.5 : Tâches réalisées par un reconstructeur d'état.

Pour ameliorer l'idee du reconstructeur d'etat precedant, nous proposons d'utiliser une methode qui consiste à tenir compte de toutes les variables aleatoires susceptibles d'integrer des erreurs dans les differentes estimations. La methode proposee est :

la méthode de Kalman.

4. RECONSTRUCTEUR D'ETAT EVOLUE DU TYPE « FILTRE DE KALMAN ».

4.1. Principe du filtre de Kalman :

Le principe adopte par Kalman consiste à adapter la valeur des paramètres de la matrice de gains K, à chaque pas d'echantillonnage. Les valeurs adaptees sont fonctions de 3 critères :

1. La confiance que l'on donne, à la determination de la première estimation par anticipation, avant correction et à la seconde estimation, après correction.

Cette confiance dépend, elle-même, de la confiance que l'on donne au pas précédent, modérée par l'erreur observée sur cette confiance.

Ce critère de confiance est traduit par Kalman par une matrice que l'on note

P.

2. Le niveau d'influence des différents bruits imposés au système, compte tenu que l'estimateur du cas précédent n'en tenait pas compte directement. Pour matérialiser ces bruits, on peut citer comme exemple sur les moteurs, les bruits occasionnés par un balourd sur le rotor qui va provoquer des à-coups de couple. On rappelle que par définition, un bruit défini un comportement aléatoire traduit sous forme de signal dont la valeur et son évolution ne peuvent pas être prédites avec exactitude.

L'influence des bruits du système, sur le filtre, est traduite par Kalman par

une matrice que l'on note Q.

3. L'influence des bruits sur les mesures qui faussent la correction de l'estimation. L'influence des bruits de mesures sur le filtre est traduite par Kalman par une matrice que l'on note R.

La méthode de Kalman fait appel à des notions de statistique (espérance, variance et covariance) que nous avons préféré présenter en annexe.

4.2. Le filtre de Kalman associé aux systèmes linéaires [14] :

Les matrices P, Q et R conditionnent la matrice de gain du filtre K. En plus des

données propres au filtre de Kalman, nous imposons les hypothèses simplificatrices suivantes :

? Les bruits imposés au système v_k et les bruits de mesures w _k sont des bruits blancs.

D'où, par définition, l'espérance de ces variables aléatoires est nulle :

E{ v_k } = 0 et E( w_k } = 0
(IV-13)

On suppose que les bruits de mesure n'auront pas d'influence sur les bruits du système et vice et versa = La matrice de variance-covariance des bruits est donc à coefficients nuls :

cvw

? ? T

= E ??? v w ??? = 0

(IV-14)

? On supposera que les bruits de mesures n'auront pas d'influence sur l'erreur initiale de la variable d'état estimée et vice et versa. D'où :

E w x ^T

??? ? ? ??? ? avec x x x

?

0 0 = 0 - ? 0/ 0

0

(IV-15)

Les variables aléatoires du vecteur « bruits de mesures » sont supposées indépendantes entre elles. Les coefficients de covariance de la matrice de variance-covariance de ce vecteur sont nuls. Seuls les coefficients sur la diagonale de la matrice (coefficients de variance) sont différents de 0. Il en est de même pour les variables aléatoires du vecteur « bruits sur le système ». D'où :

[
[

=

k

1_{0 °}T

cvv = E iv _k vk

1= E {v _k v _k^T} = Q

q1 k 0 . 0

^i1L

0 q 2k . 0

. .

q3

k

0

0 0 0 qnk

(IV-16)
et

I ,, ,, T

cww E iw _k wk

}= E w w

? ?

T ? ?

R

k k k

r₁ k 0 . 0

0 r 2k . 0

r 1 ? 1 L

i_?
? ?i

k

. .

0

r₃

rnk

0 0 0

(IV-17)

Nous venons de définir les matrices Q_k et R_k qui représentent successivement l'influence des bruits sur le système et l'influence des bruits sur les mesures.

· D'après l'expression (IV-16), on définit la matrice de variance-covariance de l'erreur sur la première estimation (avant correction) du vecteur d'état par:

T

P k / k -1 = E x k -- x k /k _₁ x k -- xk/ k _1

(IV-18)

A partir des expressions (IV-5), on en déduit une nouvelle expression :
P k k ? ? k k ? P k k ? ?

? T

?

/ ? 1 , ? 1 ? / ?

1 1 k , k ? 1 ? Q 1

d ( k ? )

Matrice de variance-covariance del'erreurr sur la1^èree estimation
(IV-19)

L'expression précédente ne suffit pas pourdéterminerrPk / k-1,' Il fautconnaîtree
l'expression deQd (k k1))qui correspond à la forme discrète de Qkk1. A partir dee

l'expression (IV-4) et des propriétés sur les variables aléatoires, on en déduit :

k

? ?

? k ? Q ? ? ? k ? d

T

v(t) v Q

d ( k -1 ) d ( k , k-1 )

? ? , ? ? ? ?

,

k- 1

(IV-20)

· Selon lecritèree des variances minimales, Kalman a pudéfinirr la matrice des gains de correction par :

K _k P k k C ? C P

T T

? C R ?

? k

/ 1

? k k

/ 1

?

-1

(IV-21)

· Dès lors, il est possible d'en déduire la matrice de variance-covariance de l'erreur sur la deuxième estimation du vecteur d'état. On obtient :

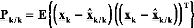
?P k / k = Pk/k-1 -- K_k C P k/k-1

Matrice de variance-covariance de l'erreur sur la 2^ème estimation
(IV-22)

Nous venons de définir la matrice P, représentant la confiance apportée aux 2 estimations du vecteur d'état et la matrice K_kreprésentant les gains de correction.

Nota :

P0/0 représente la 1^ère confiance sur l'estimation des variables d'état estimées (Matrice des conditions initiales). x0/0 : Matrice des conditions initiales du vecteur d'état du processus (moteur + machine).

x0/0 : Matrice des conditions initiales du vecteur d'état à variables estimées.

L'évolution de la matrice de gains est schématisée de la façon suivante :

Q₀

R₀

P0/0

Kk 6 y(k)

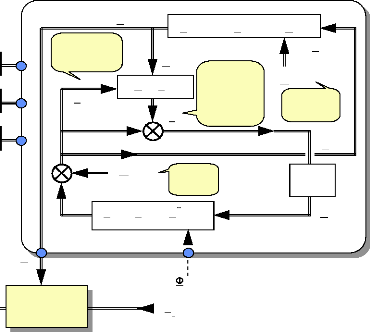
Matrice de
Gains de Correction

Matrice de Kalman

K_k

Représentatif des
erreurs sur la première
estimation des
variables d'état

+

Pk/k-1

+

(1)( k, k -1 ) P k -1 / k-1 a ( k , k-1)

K_k

Q d ( k --1)

K_k C Pk/k-1

Pk/k

+

+

K_k

?y(k)

Représentatif
des bruits
sur le système

P k / k-1 C T [ C P k /k-1 C T #177; Rk]

(k,k-1)

Représentatif des
erreurs sur la deuxième
estimation des
variables d'état

R_k

Représentatif
des
bruits de mesures

Retard

? 1

Pk/k-1

Pk - 1 /k-1

Pk/k-1

P k k E ? ? x _k x k k ? ? ? x _k x ? ? ?

T

? ? ? ? ? k / k

/ /

Fig.IV-4.1 : Adaptation des gains de correction des systèmes linéaires d'après la
méthode de Kalman.

4.3. Le filtre de Kalman étendu aux systèmes non linéaires [14][16] :

Le principal avantage de cette méthode est de pouvoir l'étendre aux systèmes non linéaires : Matrice d'évolution du système dépendante des variables d'états. Néanmoins, il est impératif de satisfaire une condition pour adapter réellement cette méthode : Connaître au moins une solution approchée du système différentiel que l'on notera xref et que l'on appellera « solution de référence ».

Tout d'abord, on admet que le système d'équations différentielles puisse se mettre sous la forme continue suivante :

t ) = f ( x ( t ), u ( t ), t ) + v ( t)

t ) = Cx ( t ) + w ( t) (inchangé )

x? (

y(

(IV-23)

On fait correspondre x 0 re f à la matrice des conditions initiales du vecteur de référence xref : Vecteur « solution approchée » du système. Le but consiste à ramener le système précédent non linéaire à un système linéaire afin d'utiliser la méthode de Kalman. Pour cela, on remplace le vecteur d'état par un nouveau vecteur, correspondant à l'écart entre le vecteur d'état et son vecteur de « référence »: x -- xref. Cela revient à faire la différence de chaque terme des 2 systèmes :

x?(t ) = f( x (t ), u (t ), t) + v (t) et ?x ref (t ) = f( x _ref (t ), u _ref (t ), t)
(IV-24)

On obtient ainsi:

x?(t ) -- *_ref (t ) = f(x (t ), u (t ), t ) -- fk _ref (t), u _ref (t), t ) + v (t)

(IV-25)

A partir de cette nouvelle expression matricielle, l'idée consiste à remplacer le 2ème membre (sans les bruits) par son développement en série de Taylor, réduit au premier ordre.

Mise en application, cela nous donne :

+

+...

v ( t)

? f x t u t t

( ), ( ),

ref

? ? ? ? ?

ref

f x t u t t f x t u t t x t x t

? ( ), ( ), ? ?

? ( ), ( ), ? ?

? ( ) ? ( )

ref ref ref

a x _ref (t)

f x t u t t

ref

? ? ?

? ( ), ( ), ? ?

ref

? u t u t

( ) ? ( )

ref

a u ref (t)

(IV-26)

Nota :

La formule mathématique de Taylor correspond à f ( b ) = f ( a ) + [( b - a) / 1 !] ? ( ) ? ... ? [( ? ) / !] ( )

f a b a n f a

n n

On peut faire une approximation, en supposant que les entrées imposent de faibles perturbations sur le système. On supprime donc le dernier terme de l'expression (IV-26). De plus, on a u_ref(t) = u(t) .

On obtient ainsi et sous une autre forme :

a[ f (x t u t t ? ? ? ? ?

f x t u t t ? ?

ref ( ), ( ),

ref ( ), ( ),

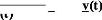
-- % ( t X 0) +

) + x( t) -- --

ref

a x _ref (t) ref a x

ref

( t)x ( t) +

(IV-27)

Or, en posant :

? ? ? ?

? f x t u t t ? ? ref ( ), ( ), F t x t , ( ) ? x ref ? x t ref ( )

: Fonction "aux dérivées partielles" de f.

(IV-28)

Et en linéarisant le système en imposant des faibles variations à x( t) autour de la trajectoire de référence x ref ( t ) (on ne tient plus compte des premiers termes de chaque membre de IV-27), on a :

x?(t ) = F_x (t, x _ref (t)) x(t)+ v (t)
(IV-29)

Si les valeurs approchées de x 0 ref sont suffisamment voisines de celles de ^?x₀ estimés

(x ₀ -- x 0 ref x ₀ -- x^?₀), on peut espérer qu'il en sera de même, à chaque instant, pour

x _ref (t ) et x^?(t ) . Dans ce cas, on remplace le vecteur de référence par l'estimation du vecteur d'état. On linéarise autour de cette estimation et le nouveau système linéarisé devient :

x?(t ) f t , x ( t ) x ( t ) v ( t )

? ? ? ?

y ( t ) = Cx ( t ) + w (t)

x t F t x t x t v t

?( ) ? ? ?

, ?( ) ( ) ( )

?

x

y t Cx t w t

? ? ? ? ? ?

? ?

?

Avec

? ? ? ?

? f x t u t t

?( ), ( ), ? ?

F t x t

x , ?( ) --? x t

?( )

On a remplacé x_ref par x?
u( t) = U :Matrice à termes constants

(IV-30)

De la même façon que pour les systèmes linéaires, on discrètise le système. On en déduit l'ensemble des équations du filtre de Kalman étendu aux systèmes non linéaires:

Processus (moteur + machine) :

x ? k k x ? x

? ? , 1 , ? ? 1

? ? v

k k d ( k ? 1 )

y k = C x k #177; w_k

(IV-31):

Avec

(IV-32) : ? ? k k x ? eF _x k k x

( , ,? )

?

, ? 1 , ? ? 1

Filtre de Kalman étendu :

1. Estimation sous forme de prédiction :

(IV-33) :		x ? ? , ? ? k k x ? 1 , ? ? ? x k k / ? 1 k k ? ? 1 1 / k k ? 1 / ? 1 y ? k / k-1 = C xk /k-1

2. Mesure des grandeurs de sortie mesurables et comparaison :

(IV-34) : ? y ? k ? = y - y --

k k k

/ 1

3. Réajustement des estimations :

? ( ? )

(IV-35) : ? x k k = x k k ? + K _k y _k - C x k / k 1

/ / 1 _

et

(IV-36) : ? y_/ C x /

k k = ? k k

4. Matrice de variance-covariance de l'erreur sur la 1^ère estimation du vecteur

d'état :

(IV-37) : P k k ( k k x ) P ( k k x ) Q

T

, ? , _ 1 , ? +

= , _ 1 ?

/ -- 1 k k

1 1

/ k k

1 1

/ k k

1 1

/ d k

_ _ -- -- _ _ ( )

? 1

Avec

(IV-38) : Q ( k k x ) Q ( k k x )

T

= , _ 1 , ? , _ 1 , ? / + Q

-- 1 k k

1 1

/ k _ 1 k k

1 1

_ _ _ _

d k

( ) k -- 1

5. Matrice de gains de correction (inchangée):

? 1

(IV-39) : K_k P k k C [ C P

^T C R ]

T

= + _k

/ 1

-- k k

/ 1

--

6. Matrice de variance-covariance de l'erreur sur la 2^ème estimation du vecteur

d'état (inchangée) :

(IV-40) : P k/ k = P k / k-- 1 -

K_k CPk /k ? 1

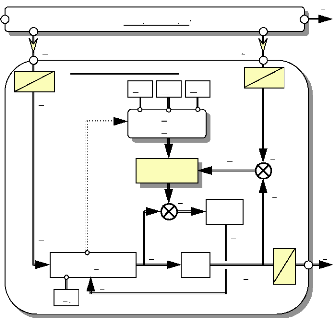
On représente le fonctionnement du filtre de Kalman étendu aux systèmes non linéaires, sous forme de schéma-blocs :

u( t)

t k

uk?1

uk?1

u( t)

c1 ( k , k _ 1 , ? xk_ 1/k_1)

x₀

Filtre de Kalman étendu

? x k_ 1/ k_1

Processus

P0/0

K_k

Gains de Correction

? x k/ k_1

+

+

Pk/k-1 Pk / k

Q₀

? x k/ k

R₀

C

Retard

6 y( k)

x ? k_ 1/ k_1

y ( t)

y k k- 1
/

?

t k

+

y_k

-

?

y k k- 1
/

k

t

y ( t)

y? ( t)

Fig.IV-4.2 :Filtre de Kalman étendu.

5. APPLICATION DU FILTRE DE KALMAN.

Pour cette etude, il est necessaire de definir les elements de l'estimateur et le referentiel avec lequel, on fera evoluer le système à variables estimees.

· L'estimateur est commande à partir des tensions d'entrees. Le couple resistant, impose par la machine entraînee, constitue l'une des variables d'entree du système = Les tensions et le couple resistant forment le vecteur d'entrée u du système. Les tensions sont mesurees et transmises, en temps reel, à l'estimateur.

Pour eviter un couplemêtre à la machine (capteur mecanique), on suppose que les caracteristiques de la machine entraînee sont connues. La machine est definie par sa constante de vitesse k repondant à la relation : Trma = kw².

· La frequence de rotation du moteur et la position du rotor seront les 2 grandeurs à estimer. Elles constituent, avec les courants, le vecteur d'état x.

· Les courants sont les grandeurs observables et constituent le vecteur de sortie y.

5.1. Choix du référentiel pour le filtre de Kalman :

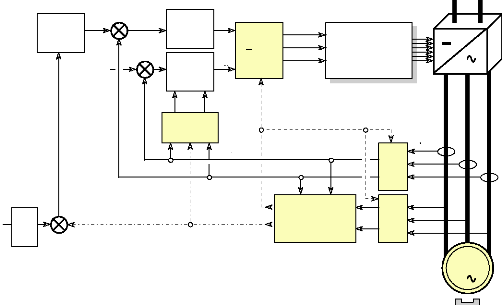
La situation ideale consisterait à utiliser le referentiel de Park avec l'axe d, cale sur le rotor. Neanmoins, cette solution n'est pas compatible parfaitement avec une commande sans capteur. Pour cela, on justifie cette remarque à partir de la figure suivante qui represente la commande du moteur dans le referentiel de Park :

+ -

_n*

2n N_p

Régulateur
de
Vitesse

+

-

eco

ids *= 0

_i*

qs

iqs

+-

ids

+-

⁶ iqs

cids

^?eds

Découpleur

Régulateur
de
Courant

ⁱqs

Régulateur
de
Courant

ids

oi

^?eqs

'vqs

^?vds

i' = i qs qs

i^?ds = ids

3

2

Oi

0

0

[ P1 ^-1

Estimateur
de Position angulaire
électrique
du rotor et de
vitesse

*

vas

vbs

*

vcs

*

iqs

Séquenceur/Modulateur

ids

MOTEUR DISCOïDE
A AIMANTS ALTERNES

Circuit
de
Commande

vds

vqs

0

[P1

[ P?

0

vcs
vbs
vas

ias
ibs
ics

MS

3

Aimants P.

Fig.IV-5.1 : Filtre de Kalman dans le référentiel de Park.

· Les 4 entrées de l'estimateur et les 2 tensions de référence en entrées de l'onduleur sont tributaires de 0^? (estimé). Or, en reprenant les équations de Park sur les courants,

on remarque que chaque terme de ces équations est fonction de ^?0. On s'imagine très facilement qu'une erreur d'estimation sur la position initiale du rotor puisse avoir des répercutions très importantes sur l'évolution du reconstructeur d'état, par rapport au système réel (cumul des erreurs). De plus, les corrections sur les erreurs d'estimation

sont tributaires des courants mesurés qui sont, eux-mêmes, dépendant de ^?0.

· On rajoute que le référentiel de Park tourne à la vitesse angulaire du rotor à partir d'une position initiale estimée. Or, une erreur sur cette première estimation peut décaler l'axe d par rapport à l'axe du rotor, avec toutes les conséquences que cela suppose. La commande vectorielle dans Park est très efficace dans des conditions normales de fonctionnement et l'est, d'autant plus dans son erreur.

La seule condition qui permettrait d'utiliser le filtre de Kalman, avec le référentiel de Park, serait d'imposer une position initiale au rotor au premier démarrage. Pour empêcher d'éliminer un trop grand nombre d'applications industrielles pour lesquelles on ne tolère pas les déplacements préliminaires, on décide d'éliminer cette solution. On se résigne à changer de référentiel. Or, le choix du référentiel de base (a_s,b_s,c_s) nécessite d'augmenter l'ordre du système et par conséquent, les temps de calculs (3 équations sur les courants au lieu de 2). On élimine aussi cette possibilité.

On propose de conserver le référentiel de Park. Néanmoins, l'axe d de ce référentiel n'est plus calé sur le rotor mais fixes par rapport à l'axe a_s. On a ainsi des grandeurs instantanées, projetées sur les 2 axes, indépendantes de la position du rotor. Ce référentiel que nous retenons pour la suite de l'étude, fait appel à la transformation de "Clarke" et utilise les repères d'axes (a_s,f3_s,o_s) et non plus (d,q,o). La commande du moteur, pour sa part, se traite dans le repère de base (a_s,b_s,c_s).

5.2. Détermination numérique des équations du système différentiel à variables estimées dans le repère (as,f3s) :

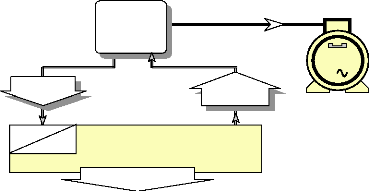
Après avoir traité en annexe 3 la transformation de Clarke, on présente le nouveau système différentiel à variables estimées et optimisées suivant :

Réseau

?

di

a

(a s,b s,cs)

(^as^,1³s )

v _as , v _bs , vcs i _as , i _bs , ics

Fi l tre de Kalman

Système à variables estimées

Cde

'11aim , R~_s,L~_s,K~_T, J~, _T~ro, T~, k~

A A

i i

as , ps

0, 6i

0, 6

MS

3

Fig. IV-5.2

s (t ) R~ ^,s

dt

s

-- si _a,s( 0+ ^ditraim 2 sind( t) + v as( t)L~L~L ss

di0

?

dt r

s

(t ) R~_s » " (t)

-- i _Ps (t)-6ittfai ^m v 2 COSO(t) + ^Ps

s

L ~ L ~

s s

d o3^s(

t ? ? ? ? ? ? ? ? ? ? ? ? ? ?

N p

? J K i t t i t

? ? t f t T T k t

? ? ? ? ? 2

~ ~ ? cos ? ? ? sin ? ? ~? ~ ~ ~ ? ? ? ?

T s

? ? s r 0

dt

A

dt

t)

_ (B(t)

(IV-41)

Avec J~ = J~_m + J~_r

Nota:

Attention aux notations, on a volontairement dissocier les variables à valeurs estimées optimisées ( (0) et les constantes estimées(~Ls).

On remarque que la présence de 6 et de 6 fait de ce système, un système différentiel non linéaire. On applique ainsi la méthode de Kalman [16]. On pose :

f x t u t t ? ?( ), ( ), ?

,

=

r 1 1 1 L

f x t u t t ? ?( ), ( ), ? 1 f x t u t t ? ?( ), ( ), ? 2 f x t u t t ? ?( ), ( ), ? 3 f x t u t t ? ?( ), ( ), ? 4

1 1 1 L

(IV-42)

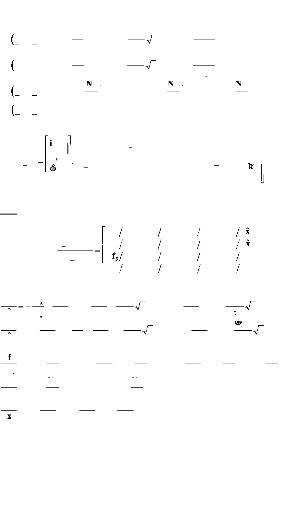
Avec :

inu n t)

= 6( 0

f₁

f₂

f₃

f₄

Et :

Chapitre 4 : Commande sans capteur mécanique du moteur et Filtre de Kalman.

I3s (
· t) -- 05( 0 11* L aim 2 cose( t ) + ^{vf" (t)}

R~

_d v5(t)

ii( 0, u ( t ), t)
ii( 0, u ( t ), t)

= -

ii( t ), u ( t ), t) = -- KT 3.( t ) sin k° + KT ; ( t )costi( t) -- ₃^p [1^-+ kdi( t)]

(IV-43)

6 ( )

t

t)1 ( t

v as v p_s

(

f 1 of 1 ⁰¹2 af1 013 af 1 a

ax1 af ₃ ai₂ af ₃ ai₃ af ₃ ai

a
a
a

4

4

4

0

Nota: v _as et v a_s sont des variables d'entrées à valeurs réelles (non estimées). On a :

f 2 af 2 a12 af 2 a13 af ^t

_as ( 0

1 0 0 =

",

Jo_s ( t )'tr [0 1 0 u ( t)

(IV-44)

, 4

ST

( t )

a

i s

( t)

0

(t)

L

i( t)

s

( V'

¹_1

af (t , i(t))

F 1(t) _

_aI(t)

af 4 ai1 af ₄ ai2 af ₄ ai3 af ₄ ai4 (IV-45)

L

Avec :

a

f₁

a

a

x₁

f₂

a

₃ Np

a x - _ KT

sin0

a ? f N N

3 p 3

f N p

? ?

t ; ? ? ~ ~ cos ? ; ? ? ? ~ ~ ?

K ? ? ?

t 2 k t

? ? ?

T

? x J ? x J

2 3

? p ~

a

J~

? f

f 3

^pitcos 6(t -- KT 3p in_Ps(t) sin e^s( t)

4

₄

a x T _Xas

f₄ f f₄

0
· -- 0 ; -- 1 ; " =0

^ -

1 a x 4 2 ax 3 ax

(IV-46)

Pour effectuer les différents calculs au moyen d'un traitement numérique, on utilise les méthodes suivantes :

- 99 -

a

-- K

--

a

a

f

a

4

R~

a f1

0
· " -- --
·
·

⁹ a x 2 t ⁹

af 2 --im 2 cos ós of

ai3 -- L~

a

f₂

R~

( t) ; -- 6( t) ^aim 2 sine( t)

a x

4 ts

; -

t a x

0 ;

af Taim 2 sin 0

af xi°

ai3 L- ~_s

x

2

t

)

;

--6(0 ^aim 2cos0(t)

s v.% #177; _as ( t)

R~

i as + 60) L 2 sin 0 ( t )

Lis L~_s

s

= -

a

a

1. Calcul de l'évolution des variables d'états f ( x^?(t ), u (t ), t) :

Méthode d'Euler ?

Evolution de

f ( X( t ), u ( t ), t ) ik / k -1 = ik -1 / k -1 + T ( k , k -1 ) * f ( ik -1 /k -1 , u_k-1 ,k -- 1)

(IV-47)

Avec

T(k,k-1) = tk-1 -- tk : Pas d'échantillonnage.

2. Calcul du vecteur de transition ?? k , k -- 1 , X) = e^Fx(...) :

Méthode des développements limités ? x 2 (Dl ( e ^x) = 1+ x+ 2 ! +... ) F1 ( t , 1( 0)^4:1^1(k , k -- 1 , ik _1 / k_1 ) = I + T ( 10k-1 ) * F ( k -- 1, ik _1 /k_1) (IV-48)

Nota : On limite la précision au 2 premiers termes du développement.

3. Calcul du vecteur de variance-covariance Qd(k-1) représentatif des bruits sur le système vd (k- 1 ) :

Méthode des trapèzes ?

v( t ) v d ( k -1 ) Q d ( k , k-1 )	k ? ? ? k ? Q ? ? ? k ? d T ? ? , ? ? ? ? ? , k-1
Q d ( k , k-1) =[4:11(k , k -- 1 ) * Q * 0^T(k , k -- 1) + Q] (IV-49)		* T( k , k-1) 2

Ces méthodes de calculs seront utilisées, par la suite, dans le filtre de Kalman.

5.3. Commande du moteur dans le repère (as,bs,cs) :

On associe au filtre de Kalman étendu une commande classique dans le référentiel (a_s,b_s,c_s). Ce paragraphe est ainsi consacré à la présentation de cette commande. On utilise une M.L.I pour le contrôle des courants et on impose une commande à couple maxi de façon à limiter au mieux les pertes magnétiques. Les équations électriques et mécaniques, du système à commander dans le repère (a_s,b_s,c_s), sont définies par les relations :

R1 ?

s aim

? ? t _L 2 sin ? ? ? ? ?

t v t
? 1

L i t _L v t ? ? ? ? ? ? ?

as as

s s s

)

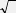
di _as (t

_ --

dt

R 1 ? ? 4 ? ?

s aim

L i t _L v t

? ? ? ? ? ? ?

? ? t _L 2 sin ? ?

t ? v ? ?

t

cs cs 3

?? ? ?? ?

3

s s s

)

di t

bs (

_ --

dt

1 ? ? 2 ? ?

aim

? ? ? ? ?

? ? t _L 2 sin ? ?

t ? v ? ?

t

?? ? 2

3 ?? ?

s

R

s

? ?

t _L v t

L i bs bs

)

di _cs (t

_ --

dt

d t

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

N p 2

? J K i t cos ? t i t

? ? sin ? t f t T T k t v t

? ? ? ? ? ? ? ? ? ? ?

?

T s

? s r 0 4

dt

d0(

dt

t) -- co( t ) + v 5( t)

Modèle du processus
Nota: Les courants des 2 repères sont liés par la transformation de Clarke (voir annexe 3).

(IV-50)

v1( t), v2( t) , v3( t) , v4( t) , v5( t) représentent les bruits du système, fonctions du temps (bruits blancs).

5.3.a) Régulation des courants ias, ibs et i_cs avec compensation des f.e.m [11] :

Contrairement à la commande vectorielle, il n'est pas possible de découpler le courant qui créé le flux magnétisant du moteur et le courant qui créé le couple. Néanmoins, pour améliorer la commande classique, nous pouvons intégrer à la régulation des courants, un dispositif de compensation des perturbations imposées par les f.e.m du moteur. On sait que la tension de la phase a_s du moteur correspond à :

di

dt

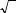
v as = R _s i _as + L_s

6)Waim 2 sin ö as

(IV-51)

6 et 0 sont les variables estimées, fournies par le filtre de Kalman.

Nous cherchons à dissocier de l'évolution du courant le dernier terme de cette expression. Il en est de même pour les autres phases du moteur.

Nota : Cela revient à linéariser les courants par rapport aux tensions d'entrées.

Concrètement, on cherche à agir sur le moteur non plus par les tensions v _as, v_bs
et v mais par les nouvelles tensions, notées u , u , et pour lesquelles, on

bs ucs

cs as

impose les relations suivantes :

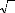
as as -- 6 T_aim 2 sinO

v bs = u_bs -- 6 T_aim 2 sin (6 -- ^27c

3

4n

v

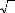
cs = u cs -- W6 _aim 2 sin (ii --

3

(IV-52)

Ainsi, le système différentiel sur les courants se simplifie et devient :

i

i

di (t)

as - R~s

_ --

dt L~

di bs (0 R~_s

_ --

dt L~

1

as (t ) + L~ u as(t)

s

s

1

bs ( t ) #177; _, u bs(t)

s

s

R~

)

i

_ --

s

cs

L~

s

di _cs (t

dt

1

(t )+ L~ u cs(t)

s

(IV-53)

On schématise le principe par la figure suivante :

Fig.IV-5.3 : Commande du moteur avec compensation des perturbations.

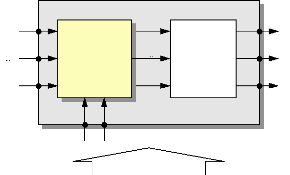
uas
ubs

ucs

Compensateur

63 6

Moteur + Compensateur
de perturbations

vas
vbs

vcs

Moteur
Fintronic

ias
ibs

ics

5.3.b) Générateur de références sur les courants [11] :

Contrairement à une commande vectorielle, les références sur les courants ne sont plus à valeurs constantes mais à valeurs sinusoïdales. Il faut créer un générateur de références pour la commande du moteur. On réalise ce générateur selon le critère optimal de fonctionnement présenté au début de ce paragraphe ; C'est à dire à couple maxi pour un fonctionnement donné.

Pour cela, il faut revenir sur l'idée de la commande vectorielle pour rappeler que
le couple maximal s'obtient pour un courant maximum porté par l'axe q du

référentiel de Park. Le principe reste le même pour notre commande, sinon qu'il n'est plus possible d'agir directement sur ce seul courant d'axe q, dissocié du reste mais sur les 3 courants du repère (a_s,b_s,cj. Une telle commande est bien trop compliquée à définir pour les régime transitoires, c'est pourquoi, on se limite à une commande élaborée sur l'unique fonctionnement du régime permanent. On présente l'idée à partir d'une construction vectorielle de Fresnel:

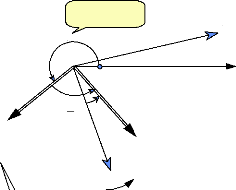
Information connue
à partir de l'estimateur

-,

V_s

0?

?

'I'

2

q

-,

I_s

a_s (fixe)

Fig.IV-5.4 : Construction vectorielle

-

D'après cette construction, on remarque que pour maintenir le vecteur courant I s

d

(? t

Vrai uniquement
en
régime permanent

(? t

suivant l'axe q (couple maxi), il est nécessaire d'imposer un décalage avance de ce
vecteur de 90°par rapport à l'axe du rotor qui lui même tourne à . Cela revient

?? t

à maintenir l'angle N' à zéro. Remarque :

Dans les cas oü les variations sur la charge sont brutales, les risques de décrochage du rotor sont à craindre. Il faut se prémunir de ce risque en maintenant ? voisin de 0 mais différent de 0..

En considérant que la position estimée du rotor est définie à chaque instant (filtre de Kalman), on peut s'imposer un courant de référence de la forme :

? ? ?

i_asréf. = I _s 2 cos ?? NJ - -

2 ? ? ?? ? i _as ré f= - I _s 2 sin ?

( ?

? ?
-

(IV-54)

Avec

? ? 0

De la même façon, on obtient les courants de référence sur les autres phases du
moteur, en les déphasant de 2t 3 et de 4 ir 3 par rapport au courant de la phase

a_s.

T i

Sachant que I 2 = max ; K étant la constante de couple, on peut alors

s T

T

représenter le générateur de références de la façon suivante :

K

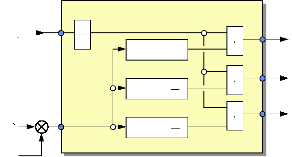
w réf

Tmax i réf

0

+

-

1

KT

Générateur de références

?

sin (d --v -- 3

sin (6' -- v -- ) 3

-- sin (6 - ? ?

.

.

.

ias

ibs

ics

réf

réf

réf

Fig.IV-5.5 : Générateur de références.

5.3.c) Synoptique de commande du moteur dans le repère (a_s,b_s,c_s) :

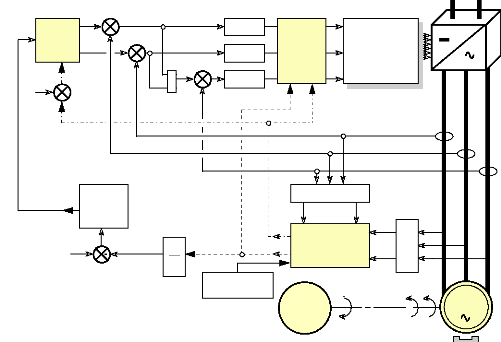
Tmax iréf

? réf

= 0

Générateur
de
références

n réf

-

+

0

i_bs réf

+-

ias réf

Régulateur
de
Vitesse
+
Limiteur

+

En

+ -

n?

T _rma= T_u = T + kifi²

-

-

1

2n

i_cs réf

+ -

??

k
Constante de vitesse
de la machine

Correcteur
PI

Correcteur
PI

Correcteur
PI

ubs vbs

uas

ucs

??

0

Compensateur
de f.e.m

Machine

i_cs

ibs

ias

Estimateur
reconstructeur d'état
FILTRE DE
KALMAN

ias

[ Cla?

0

vas

vcs

Trma

i?s

Moteur discoïde
à réluctance variable
et à aimants permanents alternés

Circuit
de
Commande

+
M.L.I

v_as

vos

T_u

[ Cla?

n

vcs
vbs
vas

+

MS

3

Fig.IV-5.6 : Schéma synoptique de la commande en vitesse et à couple maxi du moteur, muni
du filtre de Kalman.

Mémoire CNAM Patrick BOIDIN.

5.4. Validation théorique (simulation) de la commande du moteur avec filtre de Kalman :

5.4.a) Commande en vitesse du moteur avec retour de la vitesse par le filtre de Kalman (bfesmli.m + filtre1m.m en annexe 4) :

? Démarrage du moteur, soumis à un échelon de vitesse de 60 tr/min et sur une charge de la forme : T_rma = T + kw² .

Données de la simulation : (Filtre :EULER/ Moteur+Cde : EULER)/Tk=30 jis : Pas d'échantillonnage
Machine :	Régulation de vitesse :	Régulation de courant :	Variance-Covariance (coefficients sur la
J r = 0,1 kg.m2 Trma=130 N.m maxi T=0 N.m M.L.I :	?n =0,010 s kvp=20/ kvi=90 nréf=60 tr/min Conditions initiales :	kp=130 ki=65 Seuils de limit.-300/300N.m ?réf=0 Filtrage des tensions :	diagonale): P0/0 :700 (Confiance sur la 1ère estimation) Q0 : 6 (bruits sur le système) R0 : 500 (bruits sur les mesures) Bruits blancs de mesure :
	00 estimé (filtre)=0 ° 00 réel=-30 °
fp=2,4kHz(fixe)/Up=410 volts			Ib max : 0,38A pour In=9,3A Vbmax: 1,5 volts pour Vn=220 volts Bruits blancs sur le système :
		fc : 1,5kHz / Ordre : 2
			voir fichier Metafile en annexe 4.

Trma en fonction de la vitesse thétha0 réel=-30° Tem et Tr en N.m thétha0 réel=-30°

P0=700/Q0=6/R0=500/Tk=30micro sec. n (tr/min) P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a) b)

n et n estimé (- -) en tr/min. thétha0 réel=-30° theta et theta estimé (- -) en degré thétha0 réel=-30°

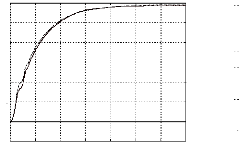
n estimée

n

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

60

50

40

30

20

10

0

-10

400

350

300

250

200

150

100

50

0

-50

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

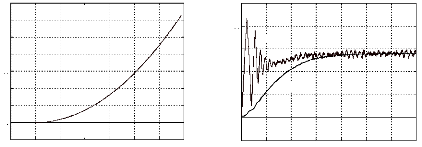
140

120

100

80

60

40

20

0

-20

-10 0 10 20 30 40 50 60

Tem

Tr

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

250

200

150

100

50

0

-50

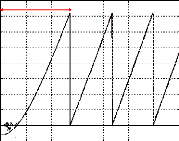
0 estimée

0

1er tour ? 27 ms

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

c) d)

Fig.IV-5.7 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.

· Les 2 caractéristiques n (t) et n _estimé (t) se suivent assez bien. La vitesse estimée est légèrement en avance sur la vitesse réelle.

Mémoire CNAM Patrick BOIDIN.

· L'erreur de position du rotor de -30°, imposée au démarrage, a été corrigée par le filtre en moins 10 ms.

Erreur sur la vitesse en tr/min. thétha0 réel=-30° Erreur sur la position en degré thétha0 réel=-30°

0.5 0 -0.5 -1 -1.5 -2 -2.5 -3		5 0 -5 -10 -15 -20 -25 -30 -35 -40
	0 0.01 0.02 0.03 0.04 0.05 0.06 0.07		0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a)
A partir de 20 ms, l'erreur sur la vitesse est
devenue inférieure à 1%.

ias et is en A thétha0 réel=-30° P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)
L'erreur sur la position du rotor est inférieure
5° sur le tour électrique.

ialpha et ibeta en A thétha0 réel=-30°

15 10 5 0 -5 -10 -15		20 15 10 5 0 -5 -10 -15
	0 0.01 0.02 0.03 0.04 0.05 0.06 0.07		0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s) P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c) d)

e)
On relève une différence notable entre les
courants i_?s et i_?s estimé d'environ #177;14%.

f)
On relève la même différence entre les
courants i ? s et i ? s estimé d'environ #177;14%.

Mémoire CNAM Patrick BOIDIN.

ias (A) / -eas (V)

60

40

20

0

-20

-40

-60

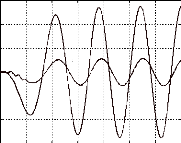
- eas

ias

vas filtrée (V) / ias (A) / -eas (V)

300

vas filtrée

- eas

0

ias

-100

-200

-300

200

100

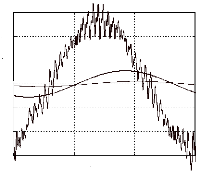
045 0.05 0.055

Temps (s)

h)

0.06

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

Temps (s)

g)
On releve un léger retard du courant sur la
f.e.m ? La commande n'est pas tout à fait à
couple maxi.

vas en volts thétha0 réel=-30°

vas en volts thétha0 réel=-30°

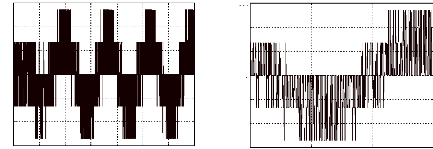
600

400

200

0

-200

-400

-600

600

400

200

0

-200

-400

-600

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

0.055 0.06 0.065 0.07 P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

i) j)

Fig.IV-5.8 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.

Les tensions telles qu'elles sont vues par le moteur, ne sont pas exploitables par le filtre de Kalman (ondes générées par la M.L.I). Il faut les filtrer.

Nota :

On a volontairement indroduit une erreur de -30° sur la position du rotor par rapport à la position estimée de 0°. On a obtenu d'assez bons résultats.

Mémoire CNAM Patrick BOIDIN.

· Démarrage du moteur soumis à un échelon de vitesse de 60 tr/min et inversion du sens de rotation sur une charge de la forme : T rma = T + kw² .

Données de la simulation : (Filtre :EULER/ Moteur+Cde : EULER)/Tk=30 jis : Pas d'échantillonnage
Machine :	Régulation de vitesse :	Régulation de courant :	Variance-Covariance (coefficients sur la
Jr =0,1 kg.m2 Trma=130 N.m maxi T=0 N.m M.L.I :	?n =0,010 s kvp=20/ kvi=90 nréf=60 et -60 tr/min Conditions initiales :	kp=130 ki=65 Seuils de limit.-300/300N.m ?réf=0 Filtrage des tensions :	diagonale): P0/0 :700 (Confiance sur la 1ère estimation) Q0 : 6 (bruits sur le système) R0 : 500 (bruits sur les mesures) Bruits blancs de mesure :
	00 estimé (filtre)=0 ° 00 réel=-30 °
fp=2,4kHz(fixe)/Up=410 volts			Ib max : 0,38A pour In=9,3A Vbmax: 1,5 volts pour Vn=220 volts Bruits blancs sur le système :
		fc : 1,5kHz / Ordre : 2
			voir fichier Metafile en annexe 4.

Trma en fonction de la vitesse thetha0=-30°

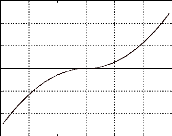
150

100

50

0

-50

-100

-150

-60 -40 -20 0 20 40 60

P0=700/Q0=6/R0=500/Tk=30micro sec. n (tr/min)

a)

n et n estimé (- -) en tr/min. thetha0=-30°

60 40 20 0 -20 -40 -60

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c)

Tem et Tr (- -) en N.m thetha0=-30°

300 200 100 0 -100 -200 -300

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)

theta et theta estimé (- -) en degré thetha0=-30°

400 300 200 100 0 -100 -200 -300

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

d)

Fig. IV-5.9 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman. Inversion
du sens de rotation

La vitesse estimée a parfaitement suivie la vitesse réelle lors de l'inversion.

Mémoire CNAM Patrick BOIDIN.

Erreur sur la vitesse en tr/min. thetha0=-30^°

0.5 0 -0.5 -1 -1.5 -2 -2.5 -3

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a)
L'erreur sur la vitesse est inférieure à
0,5tr/min soit moins de 1%.

ias et is en A thetha0=-30°

20 15 10 5 0 -5 -10 -15

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c)

Erreur sur ialpha estimé en A thetha0=-30°

10 8 6 4 2 0 -2 -4 -6 -8 -10

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

e)

Erreur sur la position en degré thetha0=-30°

5 0 -5 -10 -15 -20 -25 -30 -35 -40

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)
L'erreur sur la position est inférieure à 5°sur
le tour électrique.

ialpha et ibeta en A thetha0=-30°

20 15 10 5 0 -5 -10 -15 -20 -25
	0 0.02 0.04 0.06 0.08 0.1 P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s) d)

Erreur sur ibeta estimé en A thetha0=-30°

10 8 6 4 2 0 -2 -4 -6 -8 -10

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

f)

Fig.IV-5.10 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.
Inversion du sens de rotation

Mémoire CNAM Patrick BOIDIN.

600
400
200

0 -200 -400 -600

ias en A et eas en volts thetha0=-30°

60 40 20 0 -20 -40 -60

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a)

vas en volts thetha0=-30°

600 400 200 0 -200 -400 -600

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c)

vas filtrée et eas en volts thetha0=-30°

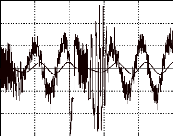
600

400

200

0

-200

-400

-600

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)

vas en volts thetha0=-30°

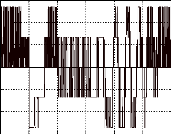
0.04 0.045 0.05 0.055 0.06 0.065

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

d)

Fig.IV-5.11 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.
Inversion du sens de rotation

· Démarrage du moteur, soumis à un échelon de vitesse de 60 tr/min. La position initiale estimée du rotor correspond à la position réelle.

Données de la simulation : (Filtre :EULER/ Moteur+Cde : EULER)/Tk=30 jis : Pas d'échantillonnage
Machine :	Régulation de vitesse :	Régulation de courant :	Variance-Covariance (coefficients sur la
Jr =0,1 kg.m2 Trma=130 N.m maxi T=0 N.m M.L.I :	?n ?0,010 s kvp=15/ kvi=40 nréf=60 tr/min Conditions initiales :	kp=55 ki=10 Seuils de limit.-300/300N.m ?réf=0 Filtrage des tensions :	diagonale): P0/0 :8 (Confiance sur la 1ère estimation) Q0 : 0,6 (bruits sur le système) R0 : 530 (bruits sur les mesures) Bruits blancs de mesure :
	?0 estimé (filtre)=0 ° O0 réel=0 °
fp=2,4kHz(fixe)/Up=410 volts			Ib max : 0,38A pour In=9,3A Vbmax: 1,5 volts pour Vn=220 volts Bruits blancs sur le système :
		fc : 1,5kHz / Ordre : 2
			voir fichier Metafile en annexe 4.

Nota:

Les coefficients des matrices de variance-covariances ont été repris pour cette simulation.

Mémoire CNAM Patrick BOIDIN.

n et n estimé (- -) en tr/min. théta0 réel= 0°

60

50

40

30

20

10

0

-10

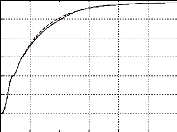
n estimé n

0 0.01 0.02 0.03 0.04 0.05 0.06

P0=8/Q0=0,6/R0=530 Temps (s)

a)

theta et theta estimé (- -) en degré. théta0 réel= 0°

0

0 estimé

0 0.01 0.02 0.03 0.04 0.05 0.06

P0=8/Q0=0,6/R0=530 Temps (s)

b)

400

350 300

250 200

150 100

50

0

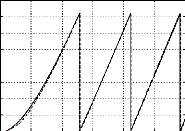
Fig.IV-5.12 Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.

5.4.b) Remarques sur les simulations effectuées.

Les dizaines de simulations que nous avons effectuées donnent de bons résultats mais dans des limites bien précises. En effet, tant que la position du rotor à l'instant initial du démarrage est restée inférieure à +ou- 90°, le moteur a démarré dans de bonnes conditions. La commande du moteur avec son filtre a rattrapé en moins de 60ms les erreurs d'estimation.

Au-delà de + ou - 90°, l'erreur initiale sur la position du rotor a été plus difficile à rattraper. Dans certaines situations, le fonctionnement du moteur est resté instable durant plusieurs secondes.

? Le filtre de Kalman, tel que nous l'avons défini, fonctionne bien, tant que l'erreur initiale sur la position est restée acceptable. Ce dispositif a besoin d'être amélioré.

A partir du moment où le filtre de Kalman a permis d'approcher, au plus vite, la trajectoire de référence (trajectoire estimée), le système réel a été capable de se coller sur cette trajectoire et d'y rester. Il suffit d'observer les résultats sur la simulation où on a inversé le sens de rotation du moteur, pour s'en persuader.

La dernière simulation montre bien que connaissant la position initiale du rotor (o0estimé =⁰0 réej, le filtre de Kalman a joué parfaitement son rôle à une faible erreur près.

Pour améliorer le dispositif, il faut :

· 1^ère idée : Imposer une position initiale au rotor, avant de démarrer le moteur.

· 2^ème idée : Détecter la position initiale du rotor par un moyen quelconque mais sans capteur mécanique.

La deuxième idée est a priori difficile à réaliser car le rotor du moteur est conçu avec une structure à pôles lisses.

Par contre, la première idée est plus réaliste et permet d'utiliser efficacement le filtre de Kalman. Par ce moyen, on peut utiliser, non plus une commande dans le repère (a_s,b_s,cj, mais une commande vectorielle dans le repère de Park (d,q).

Mémoire CNAM Patrick BOIDIN.

Le tour électrique qui équivaut à 5,625 degré mécanique est suffisamment faible pour autoriser cette idée. Les moyens à mettre en oeuvre sont simples à réaliser : Il suffit d'imposer un état à chaque interrupteur de l'onduleur de telle sorte qu'un courant continu puisse entrer dans le premier enroulement des phases du moteur et puisse sortir par les 2 autres enroulements shuntés en sortie. En imposant ces conditions et un courant continu suffisant, le rotor va se positionner naturellement suivant l'axe du premier enroulement statorique des phases du moteur.

I

as

?

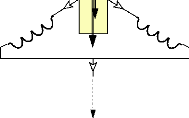
Baim

?

BI

I

Axe de la phase as

Fig.IV-5.13: Mise en position initiale du rotor par injection d'un courant continu. 5.5. Définition des moyens matériels pour les essais expérimentaux :

A défaut de pouvoir continuer cette étude, nous présentons le matériel principal et les logiciels qui auraient permis d'effectuer les essais expérimentaux :

1. Une carte multiprocesseur du type dSPACE DS1102 à multiplication par virgule flottante. Sous sa forme standard, cette carte est munie :

· Un processeur principal de signal Texas Instrument TMS320C31 (maître) ayant une fréquence d'horloge de 40 Mhz (temps de cycle : 50 ns).

· Un processeur secondaire de signal Texas Instrument TMS32P14 (esclave) pour la gestion de 12 entrées et/ou sorties numériques et pour la génération des 6 sorties M.L.I.

· 4 convertisseurs "Analogique/Numérique" (#177; 10 volts/16 bits, 10 ts).

· 4 convertisseurs "Numérique/Analogique" (12 bits, 4 ts/#177; 10 volts).

Mémoire CNAM Patrick BOIDIN.

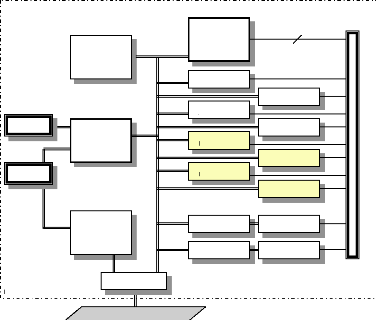
DS1102 DSP- board

Connecteur
JTAG

Interface
série

· zero wait-states

· 4 096 k Octets
de
mémoire RAM

TMS320C31

Interface
JTAG

Bus d'extension PC/AT

Interface
Serveur

Entrées / Sorties
numériques

Entrée codeur incrémental n°1

Entrée codeur incrémental n^°2

TMS320P14

Convertisseur
A/N 16 bits n°1

Convertisseur
A/N 16 bits n°3

Convertisseur
N/A 12 bits n°1

Convertisseur
N/A 12 bits n°3

Convertisseur
A/N 16 bits n°2

Convertisseur
A/N 16 bits n^°4

Convertisseur
N/A 12 bits n^°2

Convertisseur
N/A 12 bits n^°4

Filtre
d'entrée

Filtre
d'entrée

26

Connecteur E/.S A/N

Fig.IV-5.14:Carte DS1102 de Texas Instrument.

· Un interface "Codeur incrémental" pouvant recevoir 2 entrées parallèles (24 bits, 8,3 Mhz).

· Une capacité de travail de 128 kOctets sur 32 bits soit 4 M.O. de mémoire RAM.

· Un interface d'Entrée/Sortie TMS320C31 du type "série".

· Un interface d'Entrée/Sortie TMS320C31 du type "JTAG".

La carte DS1102 se connecte directement sur la carte Mère du micro-ordinateur par sa liaison bus extensible.

2. Deux capteurs de courant de Marque LEM et de type LA 25-NP (ou autres) :

· Courants nominal/maxi : 25A/36A

· Entrée/Sortie : 0-25A/0-25mA

· Alimentation auxiliaire : + et - 15volts

· Temps de retard : <1ts

· Bande passante (-1dB) : DC à 150kHz (-1dB)

· Précision à +25°C : #177;0,5% de I_n

· Montage : sur circuit imprimé

Mémoire CNAM Patrick BOIDIN.

+15 volts

'as

0 - 25A

LEM LA 25-NP

0 volts

R mesure

0 - 25mA

-15 volts

Fig.IV-5.15: Capteur de courant.

3. Deux capteurs de tension de Marque LEM et de type LV 25-P (ou autres) :

· Tension à mesurer : 400volts (Tension composée)

· Courants nominal : 10mA => Résistance R1=40k)

· Entrée/Sortie : 0-14mA/0-25mA

· Alimentation auxiliaire : + et - 15volts

· Temps de retard : 40ts pour R1 série 25k)

· Bande passante (-1dB) : DC à 150kHz (-1dB)

· Précision à +25°C : #177;1,6% de U_n

4.

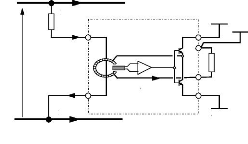
Uab

R mesure

-15 volts

'bs

'as +15 volts

R1

LEM LV 25-P

0 volts

0 - 14mA

0 - 25mA

Fig.IV-5.16: Capteur de tension.

Deux convertisseurs de signaux analogiques 0-25mA (sortie LEM tensions et courants) / -10V-+10V (entrée DS1102).

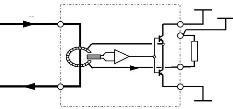
5. De 3 modules de puissance 30A dont l'ensemble constituera les 6 interrupteurs de l'onduleur (IGBT) et son interface de.

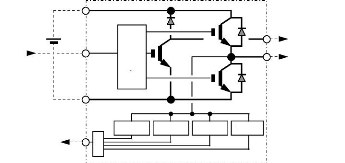
Cde
du bras

Sortie défaut

>1

Court-circuit

Cde
à
Fonctions
intégrées

Surintensité

Température
haute

UV-Lock

Frein

Phase du moteur

Fig.IV-5.17: Module de puissance d'un bras onduleur.

Mémoire CNAM Patrick BOIDIN.

Un capteur de position du type codeur absolu 12bits CHM61054C3R/4096 de marque IDEACOD Hohner AUTOMATION. Ce capteur est indispensable à la validation des paramètres de réglage du filtre. En effet, il faut s'assurer que le système à variables estimées évolue de la même façon que le moteur avant de réguler

sur les paramètres estimées ?? et 0^? .

6. Les options logiciels complémentaires à MATLAB-SIMULINK (Scientific Software - Sèvres) pour carte DS1102:

· RTW (Real-Time Workshop).

· RTI31 (Real-Time Interface).

· TRACE31W TRACE, MS-Windows (non indispensable à l'application mais bien utile).

· COCKPIT31W COCKPIT, MS-Windows (non indispensable à l'application mais bien utile).

variables Paramètres

Unité de pilotage
COCKPIT

Fig.IV-5.18

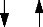
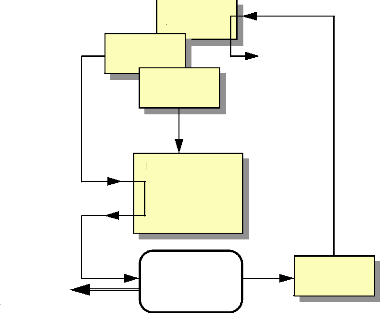
PROCESSUS
ET

SES INTERFACES

Paramètres

SIMULINK

· Cde et régulation

Interface temps réel

(Real-Time Interface)

compilateur C

(C compiler)

Téléchargeur

(Loader)

Real-Time
Workshop

MATLAB

· Filtre de Kalman

DS1102

JL C

Codage
du modèle
en "C"

Affichage des
courbes
graphiques

Enregistrement
des données

TRACE

Pour exécuter l'application avec la carte tC, il faut convertir les algorithmes de contrôle-commande écrits sous Matlab-Simulink, en langage C. De plus, il faut compiler les lignes de programme, établir les liens d'adressage avec le carte et télécharger les données.

Mémoire CNAM Patrick BOIDIN.

Ce sont les 2 premières options logiciels qui réalisent ces tâches. Il faut noter qu'il n'est pas nécessaire d'écrire les algorithmes de commande directement en langage C, le programme s'en charge avec tous les avantages que cela supposent en gain de temps et en fiabilité.

L'option COCKPIT permet de commander et contrôler le processus directement depuis le clavier du micro-ordinateur.

L'option TRACE permet de transférer les données (mesures) à mémoriser dans MATLAB de façon à analyser le comportement du processus en temps différé (Sorties graphiques sur écran).

Nous pensons que les moyens logiciels tels que nous les avons présentés ci dessus, correspondent à l'outil idéal à l'élaboration d'une commande de moteur de tous types. Il faut néanmoins préciser que ce matériel n'est pas adapté, par son coût (environ 50 000 francs), au produit final capable de commander le moteur "Fintronic". Il faudra donc après certitude sur la faisabilité de la commande étudiée, déterminer l'outil le mieux adapté aux tâches à exécuter.

La figure qui suit, présente le matériel nécessaire aux travaux expérimentaux d'une commande sans capteur mécanique du moteur.

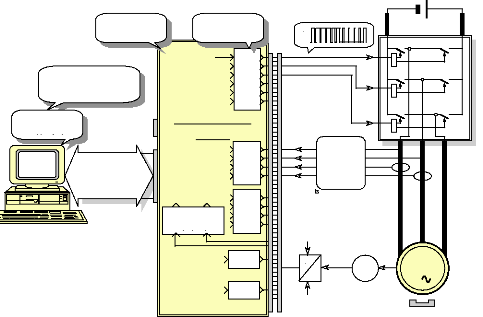
Matlab-Simulink
Version 4.2c.1
MathWorks

Algorithme de Crt/Cde
du moteur
Estimateur de position du rotor

486DX66

RTI31
Interface
Simulink/DS1102
+
Real Time Workshop

Microcontrôleurs
TMS320C31
TMS320P14

Connecteurs
liaison série

+ JTAG

12 Entrées
TTL (0-5V)
Traitement de la position

Bus PC/AT

Encoder
Phase Lines Unit

DS1102ENC

Rapport cyclique
0-100%/-1-+1

Carte dSPACE
DS1102

4 I/O TTL en réserves

Fréquences ajustables

Bit-I/O
IN ou OUT

Bit-I/O
IN

DS1102

DS1102

DS1102

PWM
Unit

ADC
Unit

DAC
Unit

PWM

AD

DA

Sub62

Alimentation TTL
0-5volts

+10 -10vol

Alimentation Codeur 0-15volts

+5v

0v

Exemple de signal en MLI

5V

15V

Interface
Signaux
Analogiques
(Convertisseurs)

Codeur Absolu 12 bits
Sortie Push-Pull 11-27V

Capteur de
position

C

t

0-25mA

I1

I2

I3

Aimants P.

vas

ias

MS

3

ibs

vbs

I'1

I'2

I'3

Capteurs de
Tension

Capteurs de
Courant

O
n

d
u
l

e
u
r

MOTEUR DISCOïDE
A AIMANTS ALTERNES

Fig. IV-5.19

Mémoire CNAM Patrick BOIDIN.

6. CONCLUSION

Cette étude a permis de démontrer qu'il n'est pas aussi évident de remplacer le capteur mécanique par le filtre de Kalman. Néanmoins, nous restons persuadé que le FILTRE DE KALMAN est le seul outil, actuel, capable de réaliser cette tâche à moindre coût.

L'inconvénient majeur de ce dispositif, tel que nous l'avons étudié, vient des conditions initiales sur la position du rotor qui conditionnent l'ensemble du système.

= Il faut impérativement trouver un moyen technique qui permettrait de connaître la position initiale du rotor. Par cette seule condition, il sera alors possible d'utiliser la commande vectorielle de PARK.

De plus, cette étude sans capteur aurait besoin d'être complétée par les études que nous n'avons pas pu réaliser dans ce mémoire. Elles sont:

· La prise en compte, dans le filtre de Kalman, des erreurs possibles d'évolution du système dues à la variation des paramètres supposés constants (résistance, flux, inductance synchrone, etc.).

· La détermination, par le calcul, de la valeur optimale des coefficients de variance des Matrices de variance-covariance.

· L'intégration dans le vecteur d'état, du couple résistant afin de l'estimer. Cas, où on ne connaît pas les caractéristiques mécaniques de la machine entraînée.

· L'étude du système à variables estimées, en limitant l'ordre du système aux seules variables à estimer (vitesse, position et couple résistant).

Cette solution risque d'être peu concluante. En effet, les tensions et les courants feraient alors partie du vecteur d'entrée avec une constante électrique élevée entre ces 2 entrées. Le système à variables d'état estimées risque d'évoluer avec un certain retard par rapport au système réel. Néanmoins, l'étude mérite d'être effectuée car le système se ramènerait à un système d'ordre 3 au lieu de 4 (avec l'estimation du couple résistant).

· L'étude complémentaire de la commande qui tient compte des cas où la vitesse du moteur est supérieure à la vitesse nominale (commande à puissance constante).

· L'amélioration technique des générateurs de M.L.I. qui est l'élément primordial de la commande avec et sans capteur mécanique de ce moteur (constante de couple élevée). De plus, il faut soigner l'entrée des courants sur le filtre car ce sont ces courant qui servent de référence à la correction des prédictions.

· L'étude des moyens permettant de détecter la position du rotor à l'arrêt bien que le moteur ait un rotor à pôles lisses.