Chapitre 3 : Commande vectorielle avec capteur
mécanique - Mémoire CNAM Patrick BOIDIN.
.
u
B
+
v
+
+
x
A
1
x
w
+
+
y
C
+
D
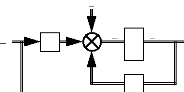
Fig. III-3.1
En utilisant la transformation de Laplace, on obtient la solution
du système différentielle à variables d'états :
X?
? ? ? ? ? ? ? ? ?
? 1
p pI A X B U p V p

? ? ? ?
i
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? 1
Y p C pI A X BU p V p
? ? ? ? ? D U p W p
?
i
(III-7)
Uniquement valable pour un systéme d'équations
différentielles linéaires.
Xi correspond à la matrice des
conditions initiales du vecteur d'état et p
l'opérateur de
Laplace.
En supposant que les conditions initiales et les bruits sont
nuls, on obtient la fonction de transfert :
|
H p Y ? p ? ? ?
? ? ? ?
? X p ? C pI ? A
|
-1
|
B + D
|
(III-8)
3.2. Choix des variables d'états :
Une commande en tension impose naturellement de
considérer les tensions comme étant les entrées et les
courants comme étant les sorties. Les variables d'états sont
généralement celles qui dérivent dans le temps. Ca sera
donc les courants. Du point de vue mécanique, l'entrée ne peut
être que le couple résistant et la sortie, la vitesse angulaire ;
La variable d'état sera la vitesse puisqu'elle dérive. Ainsi, on
pose :
di

? v ?
ds
? ?
? ?
? T ?
r

i ds
i ds
? ?
?
? ?

?
=
u v
?
? qs ?
et x
qs ?
? ?
? ? ?
?
?
i qs [I X
? d ?

ds ?
I
dt
? di ?
qs
? ?
dt
? ?
? ?
? dt ?
, y i
? ?
(III-9)
1
?
? ?
0
Rs
co
Ld
Rs
lidaim
d
L d L
ds
qs
En reprenant les équations de Park, on obtient :
I--
ds? ? ?
? 0 3
?
? 2
?
?
?
?
?
?
?
di
? ? ? ? ? _1
-co
qs
dt
di
dt
d ?
dt
? ?
2 lidaim
p J
J
?
m
f
J J
?
r m r
N
1
Ld
0 0
0
Np
J m + Jr
0 0
?
i
i
i
r
[
+
F
[
co
1
i
r
[
vds
i ?
?
? ?
vqs
i ?
? ? ? ?
?
?
Tr
1
Ld
0

(III-10)
i 1 I- 1 0 011- i i
qsI.I0 1 0L1 i 0) lj 0 0
0)
dsqs
ds
I I
(III-11)
Avec :
A
?
?
?
?
[
?
Rs
--0) _
L d _L
R
L
0
d
s
N
2 lidaim
p J + J
m
co 0
r J m -FJr
lidaim
IN 1
i
f
3
2
0 0
0 0
r
?
?
1
[
i ? ?
[
1
Ld
0
1
Ld
0
N p
J m + Jr
, B
(III-12)
|
C=
|
r
[
|
1 0 0f 0 1 0[i
0 0 1
|
: Matrice identité. D = 0
|
(III-13)
L'inconvénient de ce système vient de la matrice
A. En effet, elle présente un double
terme
non-constant (co et -co), qui nous empêche de résoudre le
système. On linéarise
donc autour d'un point de fonctionnement
oil co = c 0 , ids = Ids
0, i qs = Iqs 0 , v ds
= Vds0,
v qs = Vqs0 et T r ? T 0 r
.
Après avoir défini judicieusement les
paramètres concernés, on impose des faibles variations autour de
ce point de fonctionnement. Pour mettre en application cette solution, on
remplace :
I ds 0 + Ai ds
I qs 0 +
Aiqs
0) 0
+ Aw
V ds 0 + Av ds
V qs 0 + Av qs
T
r 0 + ATr 0

x par X 0 + Ax
r
[
1
et u par U 0 + A
u

r
? [
1 ?
?
? ?
(III-14)
A correspond à l'écart subit par
l'élément considéré, autour de son point
d'équilibre.
Après une série de transformations, on abouti au
nouveau système matriciel :
ds
d Ai
qs
dt d Ai
dt
0
dAco
? ? ? ? ?
?
?
dt
?
?
?
?
?
? ? ? ?
? ?
? L 0 Aco 0
d
Rs
?
qs

?
r
?
1 0
1 ?
?
?
0 ? ? 0 ?
L
? i ? d
? ? ? ? v

R ?
s daim
?? ? ? I
0 0 ds 0
L L
d d
? ?
? ?
?
?
xis
3
f
0
?
? ?
2
N 2 daim
p J + J
m
r
J m + Jr
ds ds
? 0 1 ?
? i ? ? v
qs qs
? ? 0 ?
? L d ? ?
?? ? T
0 ? N ?
? r 0
p ?
0 0 ? ??
J m Jr
? ?
(III-15)
Les termes Aco 0 et
--600 qui interfèrent avec l'expression des
courants, rendent lesystème toujours non-linéaire. En
considérant que la constante de temps mécanique est
supérieure à la constante électrique d'un
moteur, on peut supposer que les variables mécaniques sont
restées constantes lors de l'évolution des courants, dans le
temps.
A partir de cette remarque, il est possible d'annuler les 2
termes gênants en tenant compte uniquement des équations sur les
courants. On a:
?
qs
dt
d i
?
dt
--co0 --
ds
qs
i ds
i qs
s
d
s
d
?
?
?
? ?
d i ?
?
ds ?
?
? ?
? ? ?
?
?
R L
(0 0
R L
1 ?
?
?
?
? A
?? A
?
1_1+
? ? ?
?
?
1
Ld
0
0
1

Ld
? ? ?
?
?
? Av
?? Av
?
I_
(III-16)
Sous cette forme, il est maintenant possible de
résoudre le système à partir des équations III-7 de
Laplace. En négligeant les bruits et en considérant les
conditions initiales nulles, on a la fonction de transfert :
H (p)-
I dqs (p)
? ? ?1
? ?
pI A B
V dqs(p)
(III-17)
Avec
? ? ? ?
|
? ? I p
ds
I p ? ?
dqs ? I p
? ?
? qs
|
1 V p ?
? et ? ? ? ?
? ? ds
V p ? ?
dqs ? ? ?
? ? ? V p
qs ?
(III-18)
|
3.3. Détermination du sytème
d'équations d'états et schéma fonctionnel :
· Calcul de (pI-A)-1 :
(pI -- A) = 1 (-1)i #177;j cofacteur(
pI -- A)
det ( pI -- A)
(III-19)
Pour que la matrice pI-A soit inversible, il faut que son
déterminant soit non-nul:
1 2? ? L
Det ? pI A ? d ? dp ? p
2 1
? ? ? ? ? ?
? 2 2
1 d p d
? ?? ? ? avec ?d
2
?
2 0 2 0 ?? ?
d

? ? ?
Rs
(III-20)
L d = 53 ,7 mH
Rs = 1 , 1351 = De t(pI -- A)
= p 2 + 42 , 1 p+ 443 + co20
(I) 0
On en déduit (pI -- A) 1:
1 Fp + 1 T d ?1c?
0
? ? ? ?
pI A
? ? ??
pI A
? ? p ? d ??
det ? ?
1
0
(III-21)
· Détermination de la fonction de transfert
:
Soit, (pI -- A ) 1B = H (p) --
r 1 ? 1 ? ? ?
0
? L p d
?? ? ?? ?
1 ? L
d d
? ?
det ? ?
pI A
? ? 1 ? 1 ?
? 0
? L p d
?? ? ?? ?
? ? L ? ? ?
d d
(III-22)
On en déduit :

Rs
L2
d
? ? ? ? ? ?
R
s
L2
d
2
d
ti
0
?
0
d
?
L
?
? ? ? ?
? ?
p ? ? dp + 1
(Tdp+ 1
?
Ld
(Tdp+ 1
[ Vp
???
ds
?
V qs
( p) ?
2 d2
+ ?
1 ? ? ? ? ?
(p)
?
?
?
Ids
I qs
2
co
0
(III-23)
+
+
+
· rd
1
Lp
d
'n0
Ld
'n0
Ld
Rs L 2
d
Rs L 2
d
+
2
2
1 Lp
d
-
+
· rd
(rdp + 1)
2
I ds( p)
0
2
I qs( p)
0
2
?
·rd2 oa
2
?
·rd2 oa
(rdp + 1)
V ds ? p ?
V qs ?p)
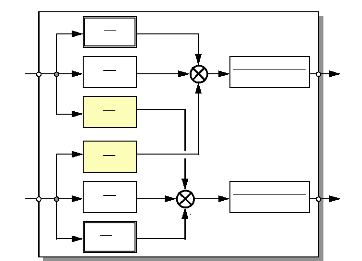
Fig. III-3.2 : Schémas fonctionnels du moteur «
Fintronic » dans le repére (d,q) Deux remarques essentielles
sont à faire :
1. Le schéma fonctionnel de la figure III-3.2, montre que
les courants de Park ids et iqs
sont liés par la vitesse angulaire au point
d'équilibre c0. L'idée consiste donc
à
intégrer, dans la régulation des courants, un
dispositif de « découplage » capable de rendre autonome les 2
boucles de régulation. Nous verrons par la suite, comment
réaliser cette fonction.
2. La condition de stabilité d'un système, est
d'avoir les pôles de sa fonction de transfert à partie
réelle négative. Dans notre cas, les pôles correspondent
aux valeurs qui annulent le déterminant de pI-A. Soit, la
résolution de l'équation :
2
p 2 + 42 + 99039 = 0
p ou sous une autre forme, ( p + R
s L d )+? 2 = 0
0
Rs
p = - #177; co0 soit
numériquement, p = -- 21 , 0 #177; j w 0
L j
d
Les pôles ont leur partie réelle négative ;
Le systéme est donc stable.
Le coefficient d'amortissement z du
systéme dépend de la vitesse au point
?
d'équilibre. Sachant que z = sin ? avec
N' = arctan , on a:
?
z =
21 ? ?
? 0
)?
1
]
? ?
sin arctan
?? ??
(III-24)
Pour une vitesse angulaire nominale de 402 rad/s, on a un
coefficient d'amortissement de 0,052 => En boucle ouverte et à la
vitesse nominale, le système est trop peu amorti, fâce
à une perturbation. Il est néanmoins stable.
Un amortissement idéal de 0,707, ferait correspondre
une vitesse angulaire de 21 rad/s (5% de la vitesse nominale) ? Il faut donc
refermer les boucles de régulation et faire appel à des
correcteurs afin de corriger, au mieux, le placement des pôles sur le
plan de Laplace.
4. ETUDE DE LA REGULATION DES COURANTS DE PARK. 4.1.
Etude du découpleur linéarisant [10]:
Le but de cette étude consiste à définir
les paramètres d'une matrice (2x2) qui
permettent de découpler
les 2 courants de Park i et i . Cette matrice
sera notée
ds qs
[Dec] et les entrées du
découpleur, U ds ( p ) et U
qs ( p) .
Fig. III-4.1
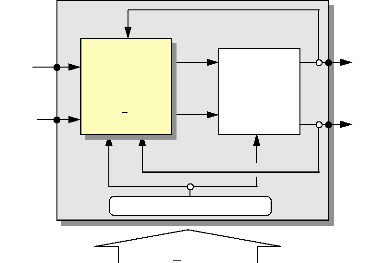
U ds? p?
U qs? p ?
Découpleur
Linéarisant
[Dec]
?
? a b ?
??
c dlj
Moteur + découpleur
H (p)
?
Point
de fonctionnement ?0
Vds( p)
Vqs( p)
Moteur
Fintronic
I ds( p)
I qs( p)
On pose :
|
[
|
Vds
Vqs
|
? ?
? ? ? ? ? ?
p ? ? U p
ds
? ? Dec ?
p ? ?
? ? U p
qs
|
1
I
J
|
Fa b1
avec [Dec] =I
L c dij
|
(III-25)
En reportant l'expression des tensions ci-dessus dans celle des
courants de III-23, on obtient :

R
s
L 2
d
0
o)
i
?
?
?
? ?
(Td p+ 1)
( ?
p1 1
? ? ? ?
? ?
p ? det pI A
?
(Td p + 1)
?
Ld
? U p
? ? ?
ds
?
U p
? ? ?
? qs ?
[
Ids
I qs
Rs L2
d
1
?
L
0
co
d
L
? a b ?
??
c dij

Rs L2
d
Ids
[
? ? ? R ?
0 s
? ?
? d p ? 1 ? ? c b ? ? ?
? d p ? 1
L L 2
? d ?
d d
co
I qs
?
? ? d
? L
? a ??
0
R s
r
[
? ? ?
0
? ? b ? d ?
? L d ?
(Td p + 1)
R
2 ? ? 1
s ? ?
d p
L
?
0
? a ? c ?
L d ?
L 2
d
d
( ?
p1
1
? ? ? ?
? ?
p ? det pI A
?
[U ds(p)1 ?
U p
? ? ?
? qs
J
(III-26)
En développant, on obtient :
(III-28)
En prenant arbitrairement a=d=1, on obtient la matrice de
découplage suivante :

(III-29)
d
? 0
?
?
?
?
?
?
? 0
1
?
? ? ? ? ?
1
?
dp
1
? D ec?
1
? d
? dp
? 2 R ?
s
0 ? ? ?
? d p ? 1
? ? 2
1 R R ?
0 s ?
? ? ? ?
p L d p
s
? ? ? ? ? ?
? ? 1 ? U p
2 qs
det pI A
? ? ? d p ? 1 ?
d
?


Ids
I
qs
D'où, la nouvelle fonction de transfert
moteur+découpleur :
Il faut annuler le dernier terme des 2 équations
précédentes. Pour cela, on résoud le systéme
suivant :

? ?
? d p ? 1
s
?
d
1
? 0
?
?
dp
?
1
d
R ?
b
s
L 2
(td p + 1 ) + d L
d
-- a L 0 ?
d
R
?
c
d
?
0
? 0
? 0
d
b
? ?
1
?
?
dp
?
1
a
?
? 0
?
c
L 2
d
? ?R ? ? ?
? ? ? ?
a L d p c L U p b
? ? ? ?
R ? ?
1 ?
s 0 s
? 1 L d p d L U p
0
? ? ? ? ? ? ? ? ? ?
1 ? ? ? ?
2 ds 2 qs
det pI A
? ? ? ? d ? ? d ? ? ?
d d
Ids
I qs
? p =
(III-27)
?
1 ? ? R ? ? ? R ?
0 s 0 s
? ? ? ?
p ? ?
? ? b ? d ? ? ? ?
? d p ? 1 ? ? ?
U p ? a ? c ? ? ? ?
? d p ? 1 ? U p
qs ds
pI A
? ? L L 2 L L 2
det ? ? d ? ? d ?
d d
1 ?
? ?
? R ? 2 R ?
0 s
? d p ? ?
1 ? 0 ?
? dp ? 1 ?
?
? ?

I dqs \p /td2
?
s ?? L 2
H
? p --

? d
2
0 Rs

? ? ? ? 2
U p ? ? ? ? ?
?
2 2
dp d ? R
1 s
dqs 0 0 ? ?
ti
? 1
dp
?
? d p ? 1
? ?
L2
d
(III-30)
En reprenant l'expression III-25, on obtient :
Découpleur linéarisant.

d
t
1
w 0
?
1
t
+
dp
1 ?
1
1 i
d
1 ? L
t
1
w 0
1
dp
t
+
? V p
? ? ?
ds
?
V p
? ? ? ?
? qs ?
? U p
? ? ?
ds
?
U p
? ? ?
? qs ?
(III-31)
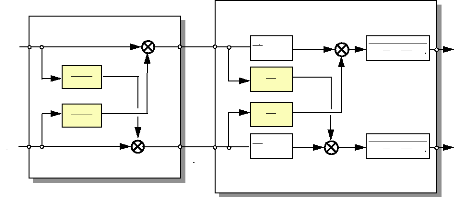
On obtient ainsi sous forme de schéma fonctionnel, le
moteur FINTRONIC muni de son découpleur fonctionnant autour de
c0 :
Fig. III-4.2
R
L2 d
Rs
L2 d
s
(ndp+ 1)
(ndp+ 1)
w0
Ld
w0
Ld
+
+
-
+
p 2 + ? 2
2 0
d p d
? ?
? ?
p 2 + ? 2
2 0
d p d
? ?
? ?
1
2 1
1
2 1
+
tdp+ 1
030T
d
-
d
030T
T
1
dp+
+
+
U ds? p)
U qs( p)
Vds( p)
Vqs( p)
I ds( p)
I qs( p)
Pour mieux comprendre le rôle du découpleur et
vérifier son efficacité, nous avons effectué une
série de simulations avec le système fonctionnant en boucle
ouverte pour une vitesse de rotation donnée,
c0 constant. D'après les résultats
obtenus, le dispositif a bien rempli ses fonctions de découplage. En
plus, il a permis de supprimer les oscillations de courant qui ont eu tendance
à augmenter avec co0. En contre partie, on fait les
remarques suivantes :
· Ce type de découpleur, impose d'estimer les
paramètres Ld et Rs de la
machine. Il faut donc connaître les paramètres du moteur.
· 03 est constant que durant un laps de
temps. Or, les courants ne disposent que de 72ms environ (constante
mécanique) avant que la vitesse angulaire n'évolue et rende le
système non linéaire. Le découpleur réduit les
oscillations mais ralentit la progression des courants.
4.2. Autre solution de découplage :
A partir des équations électriques de Park
çi dessous, on propose une autre solution de découplage des 2
courants [11].
v ds = R s i ds Ld --
e
di ds
dt ds
di
v qs = R s i qs Ld dt +
e qs
(III-32)
La solution consiste à remplacer v
ds par uds -- e~ds et v
qs par uqs + e~qs , de
façon à obtenir les deux nouvelles expressions suivantes :
? Chaque courant dépend uniquement de sa propre
tension
u ds = R s i ds Ld
u qs = R s i qs Ld
ds
di
dt

ds
di

dt
(III-33)
Avec ~eds et
e~qs : variables à paramètres estimés.
Or, pour valider cette expression, il est essentiel que
~eds puisse correspondre à chaque instant
à e ds et ~eqs
à e qs.
Sachant que e ds ? ? L d i
qs et e qs ? ? ? L d i ds ? ??
daim ? , on remarque très vite que la
qualité
du découplage dépend essentiellement de la qualité des
paramètres estimés
~
~Ld, 'daim et de la
précision de mesure de la vitesse angulaire w.
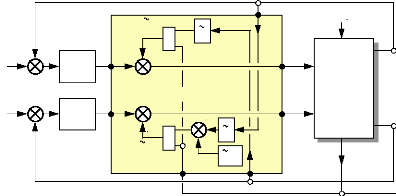
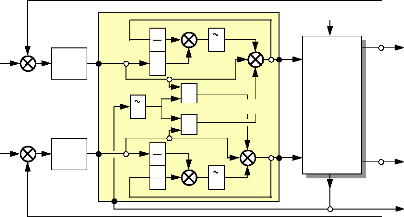
On représente les 2 solutions de découplage par
les schémas blocs suivants :
ids*
i qs
*
ids
iqs
+
+
-
-
PI
PI
uds
uqs
+
+
eqs
eds
+
-
Découpleur
.
.
03
03
+
Ld
+
4,daim
Ld
vds
vqs
Moteur
Fintronic
Trma
?
iqs
?
ids

Fig.III-4.3 : Découpleur de la
2ème proposition.
ids*
i qs
*
ids
iqs
+
+
-
-
PI
PI
uds
uqs
Co
td
d
dt
d
dt
d
dt
d
dt
-
-
.
.
+
+
Découpleur
td
td
+
+
+
+
+
-
vds
vqs
Moteur
Fintronic
Trma
?
i ds
iqs
?
?
Fig. III-4.4 : Découpleur de la
1ème proposition.
4.3. Etude comparative des 2 découpleurs
:
Les 2 solutions proposées peuvent être
résumées schématiquement de la façon suivante :
Solution n°1 Solution n°2
ids
Découpleur n°1
Dérivation des entrées
et des sorties
Ld Rs
Ld
??daim
vds
vqs
Découpleur n°2
Pas d'action
dérivée
? iqs
Fig.III-4.5
· Les valeurs estimées sont
Ld et Rs dans la
première solution et Ld,
Tdaim dans la
seconde.
· Il paraît plus facile de
prédéterminer la variation de la résistance statorique
Its en fonction de la température que le flux
créé par les aimants en fonction de cette même
température.
· La seconde solution nécessite 2 entrées
supplémentaires ids et
iqs.
Les erreurs faites sur les mesures de courant sont
multipliées par 2.
La première solution impose de dériver les
entrées/sorties pour découpler les courants. C'est
l'inconvénient de cette solution.
En conclusion, il est difficile de choisir entre les 2
solutions proposées, sans les tester réellement. Elles ont
chacune leurs avantages et leurs inconvénients et il faudrait continuer
l'analyse pour en favoriser une. La proposition n°2 paraît la plus
simple à réaliser et sera retenue pour la suite de cette
étude.
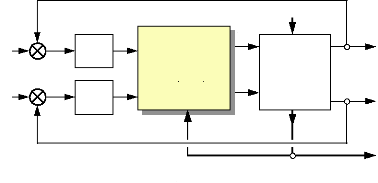
4.4. Boucle fermée avec correction sur les
courants :
Maintenant que nous avons choisi un type de
découpleur, nous pouvons refermer la boucle de régulation des
courants de Park à travers des correcteurs P.I. On schématise
l'ensemble :
Trma
ids*
i qs
*
i ds
+
+
-
-
PI
PI
Découpleur
Linéarisant
vds
vqs
Moteur
Fintronic
i ds iqs
iqs
0)
0)
Fig.III-4.6
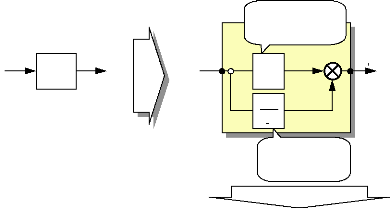
E ( p)
S( p)
+
Kp
+
K
p
i
Action proportionnelle
Dicte la rapidité de
réaction de
la
boucle
Action intégrale
Elimine l'erreur entre la
référence et la
sortie
En valeur instantanée :
PI
S( p)
E ( p)
s ( t) = K p e ( t) + Ki?e ( t)dt
Fig.III-4.7
Avec
5. REGULATION DE VITESSE.
5.1. Choix d'une régulation de vitesse [8]
:
Parmi les 2 types de régulation, proposés par
les figures III-5.1 et III-5.2, on utilisera celle qui est la plus
utilisée pour les entraînements de machines. C'est à dire,
la régulation à boucles multiples montées en cascade.
|
|
|
|
|
|
|
|
|
vds
vqs
|
Convertisseur
+
Moteur
Fintronic
|
|
Régulateur
de
vitesse
|
|
|
|
+
|
|
|
Régulateur
de
courant
|
|
|
Limiteur à seuils
|
|
-
|
|
|
|
|
|
|
ids i qs
|
|
|
|
|
|
|
|
|
|
|
|
+
0)*
0)
Fig.III-5.1 : Régulation à boucles multiples
en cascade.
(*
ids*
i*
qs
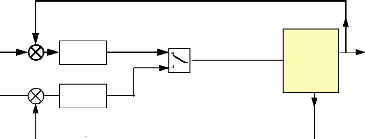
+
+
-
-
ids i qs
Régulateur
de
vitesse
Régulateur
de
courant
Commutation
vds
vqs
Convertisseur
+
Moteur
Fintronic
CO
Fig.III-5.2 : Régulation à
boucles en parallèles.
5.2. Schéma-blocs de l'ensemble
Moteur/Machine/Régulations : A partir des équations
mécaniques et électriques en III-34,
T em -- Tr
|
N ? J J ? d
1 ? ?
? ?
? dt f
? ?
m r
?? ??
p
|
|
T r = T r 0 + Trma T rma = T + kw
2 Tem = K T iqs
(III-34)
On obtient l'expression de la variation de vitesse du moteur
:
(KT i qs -- T r0 -- T) --
N k
p
co -- o)
J m + Jr J m + Jr
2
f
Np
do)
dt
J m + Jr
(III-35)
Traduit sous forme de schémas blocs et muni des boucles
de régulation Courant/Vitesse, on a le schéma suivant :
Limiteur à seuils
Fig. III-5.3
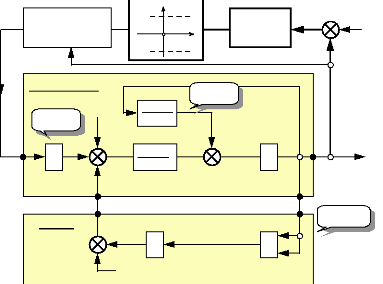
Régulateur
de courant avec
iqs
découpleur
Moteur Fintronic
Constante
de couple
Machine
KT
+
+
Tr0
?
Trma
-
-
+
iqs*
T
Imax
Imin
N p
J J
m + r
f
J m + J r
k
(A)
Frottements
visqueux
t
+
-
?2
Correcteur
PI
J
.
Equation
machine
+
-
(0*
0)
En supposant que découpleur joue efficacement son
rôle, on remarque que le courant ids n'intervient pas
directement sur le couple électromagnétique. On se retrouve dans
les mêmes conditions qu'une machine à courant continu.
Pour cette régulation, on utilisera un correcteur de type
Proportionnel-Intégral identique à la régulation des
courants.
Pour compléter la chaine de régulation, il est
nécessaire de rajouter un dispositif de limitation des variations
brutales de la consigne de vitesse. En effet, si le moteur est capable de
réagir très vite à un changement de consigne sur la
vitesse, il n'en est pas forcément de même pour la partie
mécanique de l'ensemble moteur/accouplement/machine.
Le moyen utilisé, pour réaliser cette fonction,
est un filtre du 1er ordre dont la
constante de temps 'E
est imposée en fonction de la rapidité souhaitée
et en fonction
n
des contraintes mécaniques à limiter. Si on
appelle n l'entrée du filtre et n
la
*
ré f
sortie du filtre, la fréquence de rotation obéit
à la loi :
* dn * dn*
n + t n ?
n ré f
dt
1
= (n n * ) : Filtre du 1er
ordre.
ré f ?
?
dt
n
(III-36)
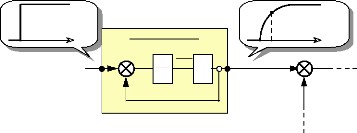
nréf
t
Filtre du 1er ordre
nré f
+
1
tn
dn
dt
*
J
-
n*
+
Cn
nré f
? n t
-
n
Fig. III-5.4
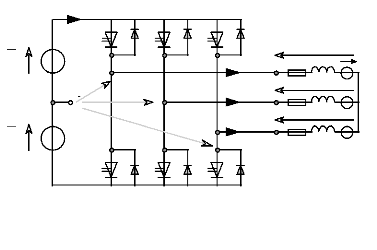
6. ONDULEUR DE TENSION.
6.1. Généralités :
Pour commander le moteur, il est nécessaire d'interposer
entre la commande et le moteur, un dispositif de puissance :
L'onduleur de tension controlé en courant.
1
3
2
2
ias
Ls
Rs
va0
+
U
i
v cN = v cs
va0
U
2
0
vb0
vc0
ibs
ics
vb0
vc0
eas
N
ebs
ecs
-
1'
2'
3'
Fig.III-6.1
- 71 -
v aN = v as
v bN = vbs
+
+
Ceci nous amène à parler de la modulation de
largeur d'impulsions dont le rôle est de reconstituer au mieux une
onde sinusoïdale à partir d'une tension continue. Bien qu'il
existe, à l'heure actuelle, une multitude de variante d'ondes en M.L.I,
nous proposons une M.L.I dite « naturelle » à temps
réel. Elle se réalise, soit par un traitement analogique du
signal de commande qui est simple à réaliser mais limitée
dans ses possibilités, soit par un traitement numérique qui offre
des possibilités, bien supèrieures, adaptatives au fonctionnement
du moteur. En contrepartie, cette dernière solution nécessite des
moyens de calculs plus puissants donc plus onéreux (multiprocesseurs).
L'onduleur utilisé est généralement un onduleur de tension
triphasé en pont, constitué de 3 demi-ponts. Il est
schématisé de la façon suivante :
Le point 0, représenté sur le schéma,
est évidemment fictif. Il est uniquement utilisé par
commodité et permet, dans la représentation schématique,
d'obtenir une symétrie sur les ondes de tensions v
a0 , v b0 et v
c0 suivant l'axe des temps.
Sachant que l'expression des tensions aux bornes de chaque phase
du moteur est la suivante :
v v
= =
aN as
v v
= =
bN as
v v
= =
cN as
|
1 3 1 3 1 3
|
( 2 v v v
- - )
a 0 b 0 c 0
( +
v 2 v v
- )
a 0 b 0 c 0
? ? - +
v v 2 v )
a 0 b 0 c 0
(III-36)
|
|
Les tensions v , et v ne
peuvent prendre que 2 valeurs de potentiel : +U/2 et -
a0 vb0 c0
U/2. Il suffit d'appliquer une séquence de commande
des interrupteurs spécifiques à une commande du type
à modulation de largeur d'impulsions pour obtenir les
formes d'ondes de tension que l'on souhaite :
6.2. Onduleur à commande en M.L.I :
Pour l'ensemble des simulations, on utilisera une Modulation
de largeur d'impulsions basée sur le principe de la comparaison des
signaux de commande en tension du moteur avec celle d'un signal triangulaire de
fréquence fixe. Cette fréquence, m fois supèrieure
à la fréquence nominale, correspond à l'indice de
modulation de la M.L.I. Sa valeur sera entière et multiple de 3 de
façon à faire correspondre, à chaque période, la
forme du fondamental de l'onde à reproduire.
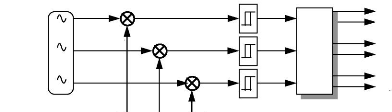
La M.L.I que nous utiliserons, se schématise de la
façon suivante [12] :
Bascules de Schmitt
Tensions de
référence
Modulatrices
v M (t )
v P (t )
+
-
+
ebs1(t)
sbs1(t)
-
+
-
Commande
logique
cI1(t) cI1'(t)
I1
I1'
I2
I2'
I3
I3'
Porteuse
Tensions à
dents de scie
Fig.III-6.2
0 0.005 0.01
0.015 0.02 0.025
0.03
TP
VM
TM
VP
ebs1 : Entrée de la bascule
sbs1 : Sortie de la bascule
0 0.005 0.01 0.015 0.02 0.025 0.03
500 400 300 200
100
0
-100 -200 -300 -400 -500
800
600
+10 400
200
t 0
-200
-10 -400
-600
-800
|
|
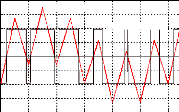
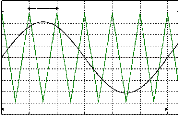
t
a) Ondes de tension de la modulatrice et de la b) Ondes de
tensions d'entrée et de sortie
porteuse d'une bascule
Fig. III-6.3
TM : Période de la
modulatrice ? 0,42 ms. TP : Période de la
porteuse ? 30 ms.
6.3. Commande en couple avec un onduleur de tension
à M.L.I ; Simulations.
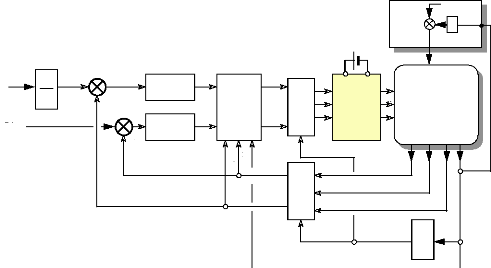
Idsref = 0
Tn*
1 KT
iqsref
+
-
+
6 iqs
bids
-
ids
Correcteur
PI
Correcteur
PI
uds
u qs
Découpleur
linéarisant
iqs
ids
?
?
i?ds -- ? ids
i?qs - iqs
v ? qs
'vds
?
0
[ P1 -1
[ P1
vMas
vMbs
vMcs
Onduleur
+
Cde
logique
U
vas
vbs
vcs
Machine
ias
ibs
ics
Modèle du moteur
discoïde à
réluctance
variable et
à aimants permanents
0
?
+
+
Trma
?
T
k
?
co
Fig.III-6.4 : Schéma synoptique de
la commande en couple du moteur
FINTRONIC.
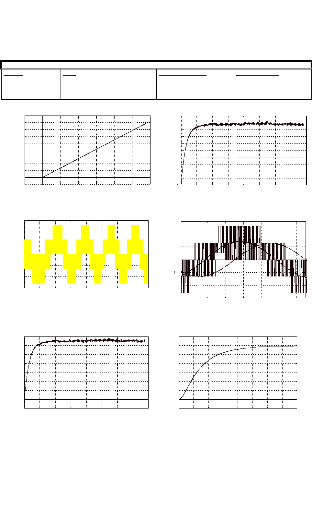
C a r a ctér istiq u e d e la machine e n tr a in
ée
(N .m )
(N .m )
Chapitre 3 : Commande vectorielle avec capteur
mécanique - Mémoire CNAM Patrick BOIDIN.
.
· Simulation n°1: Démarrage du moteur
sans à-coups de charge.
|
Données de la simulation : Commande en
couple.
|
|
Machine :
|
M.L.I :
|
Régulation de courant :
|
Conditions initiales :
|
|
Jr =0,2 kg.m2
T=0 N.m
k=0,408 N.m/rad.s-1
|
Fréquence de la porteuse : 2,4kHz Indice de modulation m
:48
|
Cdp=35 / Cdi=200 Cqp=17/ Cqi=350
*
T = Tn = 176 N .m
|
00 = 0 °
|
6 0 0
4 0 0
2 0 0
0
-2 0 0
-4 0 0
-6 0 0
vas
m 0 .0 1 0 .0 2 0 .0 3 0 .0 4 0 .0 5 0 .0 6 0 .0 7 0 .0 8
Tem p s (s )
d) Tension aux bornes de la phase as du
moteur :
vas( t ) .
(A )
iq s
0 0 .0 1 0 .0 2 0 .0 3 0 .0 4 0 .0 5 0 .0 6 0 .0 7 0 .0 8
T e m p s (s)
1 4
1 2
1 0
8
6
4
2
0
-2
2 0
1 0
-1 0
-2 0
1 8 0
1 6 0
1 4 0
1 2 0
T r m a (n )
1 0 0
8 0
6 0
4 0
2 0
0
-2 0
-1 0 0 1 0 2 0 3 0 4 0 5 0 6 0
F ré q u e n c e d e rotation (tr/m in )
a) Caractéristique de la machine
entraînée.
Trma ( n)
(A ) (V )
2 0 0
1 8 0
1 7 6
1 6 0
1 4 0
1 2 0
1 0 0
8 0
6 0
4 0
2 0
0
Tref
Tem
0 0 .0 1 0 .0 2 0 .0 3 0 .0 4 0 .0 5 0 .0 6 0 .0 7 0 .0 8
Temps (s)
b) Couple électromagnétique:
Tem( t ) .
(A ) (V )
600
400
00
0
00
-400
-600
0.066 0.068 0.07 0.072 0.074 0.076 0.078
vMas
vas
ias
10
-10
Temps (s)
e) Modulatrice de tension de la phase a ,
s
tension et courant :v Mas ( t ) , v as ( t
) et i as( t)
(tr/m in )
70
60
50
40
30
20
10
0
-10
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08
T em ps (s)
n
g) Evolution de la fréquence de rotation du moteur lors
de la phase de démarrage: n( t ) .
Fig. III-6.5 : Résultats des simulations. Commande
en couple du moteur.
· La M.L.I provoque des oscillations de couple de #177;
5N.m (#177;2,8%) autour de 176N.m.
· La fréquence de commutation imposée par la
M.L.I est de 2,4kHz.
- 74 -
f) Courant de Park sur l'axe q : i qs ( t )
.
| 


