Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

C

bs

cs

Décision prise
à l'instant considéré

-->

I s

as

i

Point de référence

S

Axe du flux
statorique

?

N

? i

a

S

i

-->

? aim

N

Axe rotor

Le rotor tend à vouloir s'aligner avec
l'axe du flux statorique

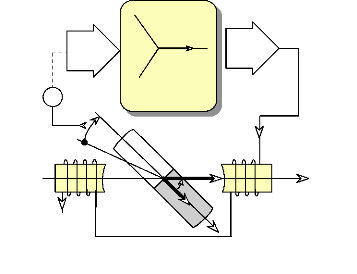
Fig. III-2.2

Analyse

de la situation
à l'instant
considéré

Mise en
application de la
décision
prise

Capteur de
position
du rotor

La figure III-2.2 représente, sous une forme simplifiée, le principe de fonctionnement du moteur synchrone à aimants permanents avec son autopilotage.

2.4. Contrôle par la tension du couple électromagnétique :

Le moteur est commandé en tension. Il faut donc exprimer le couple électromagnétique
en fonction de v _qs et non plus en fonction de i_qs. On obtient ainsi, à partir des équations

suivantes :

qs

di ds

v R i L

? ? ? ? L i

ds s ds d d

dt

v qs = R s i qs Ld

di dt^qs +coL di

? ?ds Wdaim

1

T em -- T r = ( J _m + J_N

p

iqs

? d ? ?

dt f T K

r ) ? ? ?

Avec

?? ?? em T

(III-2)

la nouvelle expression,

K_T di qs

T _em =v -- L

R qs ^d dt --0 L _d i ds -- ⁽¹⁾¹Pdaim

s

(III-3)

qui est devenu dépendant non seulement de v mais aussi de et de la variation de

ids

qs

iqs

.

Pour supprimer une partie de cet inconvénient, on impose un courant i nul au moyen

ds

d'une régulation sur ce courant avec une référence nulle. En supposant que la vitesse est restée constante durant la perturbation, on obtient alors :

Tem

K ? di

T qs

= R v L

?? - ? ?₀ ?

qs d daim

dt

s

(III-4)

On a ainsi une équation différentielle à coefficients constants facilement résolvable de la forme :

i qs

L di v

d qs qs ? O)0 " daim

+ ?

R dt R R

s s s

(III-5)

Nota:

Cette condition est indispensable pour définir les paramétres d'un correcteur du type PI qui de par sa nature gére des systémes uniquement linéaires.

3. MODELE D'ETAT DU MOTEUR ET CHOIX DES VARIABLES D'ETATS.

3.1. Définition et notations :

Tout système linéaire, continu et à variables multiples, peut être représenté par le modéle d'état suivant :

x? Ax Bu v

= + +

y Cx Du w

= + +

(III-6)

Avec

A : Matrice (n,n) d'évolution du système.

B : Matrice (n,ne) d'application de la commande.

C : Matrice (ns,n) de sortie du système.

D : Matrice (ns,ne) d'action directe sur le système.

x : Matrice d'état.

x? : Matrice dérivée de la matrice d'état.

u : Matrice d'entrée.

y : Matrice de sortie.

v : Bruit d'état du système. Ce vecteur représente les incertitudes de la modélisation.

w : Bruit de mesure du systéme. Ce vecteur représente les bruits affectés par les différents capteurs des grandeurs mesurées.