Impact des crédits a l'économie sur l'inflation et la croissance au Bénin

A- Analyse des données des modèles :

® Test de normalité de Jarque Bera

Le test de normalité de Jarque Bera effectué sur les variables (voir annexe 3) indique que seules les séries PIBR, CE, et INVESTOTR du Bénin sont normales et lognormales sur la période de 1972 à 2003. En effet, au seuil de 5% l'hypothèse de normalité est vérifiée (JB<5,99 ou Probability >0,05)

Le tableau présenté à l'annexe n°3 résume les résultats de ce test

® Tests de racines unitaires

Le test de Dickey-Fuller Augmenté (ADF) est utilisé pour déceler la présence éventuelle de racines unitaires. Le test sur les variables en niveau est effectué avec tendance et constance alors que le test sur les différences premières des variables est réalisé uniquement avec la constance. De ce fait, l'hypothèse alternative pour le test sur les variables en niveau est une tendance stationnaire avec une constance non nulle alors que l'hypothèse alternative pour le test sur les différences premières des variables est la stationnarité avec une constante non nulle.

Le tableau ci-après présente les résultats des tests de racine unitaire.

Tableau 1 : Test de racine unitaire sur l'ensemble des variables du modèle

	Test à niveau			Test en différence première			Conclusion
Variables	ADFc	ADFt	Retard	ADFc	ADFt	Retard
INFL	-3.1	-3,57	1	-576	-3.57	1	I(1)
CE	-0.41	-3.57	1	-2	-1.95	1	I(1)
INVTOTR	-0.92	-3.57	1	-4.26	-1.95	1	I(1)
PIBR	-2.09	-3.57	1	-4.48	-1.95	1	I(1)
TXCHANGE	-0.32	-1.95	1	-6.06	-1.95	1	I(1)
LCE	-2.22	-3.57	1	-2.62	-1.95	1	I(1)
LINVTOTR	-1.59	-3.57	1	-4.79	-1.95	1	I(1)
LTXCHANGE	-1.13	-2.96	1	-5.02	-3.57	1	I(1)
LPIBR	-3.08	-3.57	1	-4.63	-1.95	1	I(1)

Source : Traitement Eviews

Il apparaît que toutes les variables sont intégrées d'ordre 1 (I(1)) puisque leurs différences premières sont stationnaires. On peut donc envisager l'étude de la cointégration des variables et proposer, au besoin, un modèle à correction d'erreur pour estimer chaque équation.

B - Estimations des équations :

L'objectif de l'étude n'est pas de parvenir à identifier dans leur diversité, l'ensemble des variables qui influence l'inflation et la croissance, mais de mettre en relief celles, qui de par leurs effets conjugués, expliquent l'impact des crédits à l'économie sur ces deux indicateurs macroéconomiques.

B 1 - Estimation de l'équation dinflation

a- Test de cointégration

Ce test n'est utilisable que si les variables sont du même ordre d'intégration. Ce qui est le cas ici. En effet, toutes les variables de l'équation d'inflation sont I(1).

Pour tester la cointégration des variables du modèle d'inflation, deux méthodes sont envisageables : la méthode de Engle et Granger et la méthode de Johansen. Nous utiliserons la méthode de Engle et Granger. Ce test se déroule en deux étapes :

1ère étape : Estimation par les M.C.O de la relation de long terme.

L'observation de l'évolution du taux d'inflation indique un choc en 1975 et 1994. Le choc de 1975 résulte des perturbations sur l'économie béninoise qu'a entraîné le premier choc pétrolier. Ce modèle intègre à cet effet, deux variables muettes D75 et D94 prenant les valeurs 1 respectivement en 1975, 1982 et 1994 et la valeur 0 ailleurs.

La cointégration des différentes variables contenues dans le modèle est établie lorsque le résidu issu de l'estimation est stationnaire, c'est-à-dire lorsqu'il est I(0). Le test ADF est donc appliqué sur le résidu de l'équation de long terme.

2ème étape : Test ADF sur le résidu

ADF Test Statistic -3.358824 1% Critical Value* -3.6852

5% Critical Value -2.9705

10% Critical Value -2.6242

Source : Traitement Eviews

Le test ADF effectué sur le résidu indique que les séries INFL, LCE, LPIBR et LTXCHANGE sont cointégrées.

Ce résultat est du reste confirmé par le test de Johansen qui montre l'existence d'une seule relation de cointégration.

Tableau 2 : Résultat du test de cointégration de Johansen

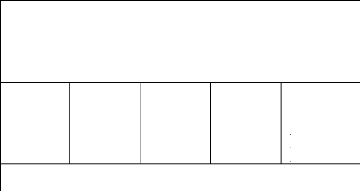
Date: 07/29/04 Time: 11:30

Sample: 1972 2003 Included observations: 29

Test assumption: No deterministic trend in the data Series: INFL LCE LPIBR LTXCHANGE

Lags interval: 1 to 2

Eigenvalue Ratio

*(**) denotes rejection of the hypothesis at 5%(1%) significance level L.R. test indicates 1 cointegrating equation(s) at 5% significance level

0.651417

0.505114

0.259094

0.139864

Likelihood

4.369278

64.02776

33.46525

13.06585

5 Percent

Critical Value

53.12

34.91

19.96

9.24

Critical Value

1 Percent

41.07

24.60

60.16

12.97

Hypothesized

No. of CE(s)

At most 1

At most 2

At most 3

None **

Source : Traitement Eviews

Sur la base du résultat de ce test, nous pouvons donc utiliser la représentation à correction d'erreur proposée par Engle et Granger.

b) Estimation du modèle à correction d'erreur

En ce qui concerne l'inflation, l'équation du mécanisme de correction d'erreur s'écrit :

D(INFL) = C(1) + C(2)*D(LCE) + C(3)*D(LPIBR) + C(4)*D(LTXCHANGE) + C(5)*INFL(-1) + C(6)*LCE(-1) + C(7)*LPIBR(-1) + C(8)*LTXCHANGE(-1) + C(9)*D75 + C(10)*D94 + [AR(1)=C(11)]

Dans cette expression, les coefficients C(2) à C(4) représente la dynamique de court terme, tandis que les coefficients C(6) à C(8) permettent de dériver les comportements d'équilibre de long terme. Le coefficient C(5) est le coefficient de correction d'erreur. Il représente la force de rappel vers l'équilibre du modèle. Il doit être négatif, dans le cas contraire il convient de rejeter la spécification de type ECM (Modèle à Correction d'Erreur).

Les signes théoriques ci-après sont attendus :

Paramètre	C(1)	C(2)	C(3)	C(4)	C(5)	C(6)	C(7)	C(8)	C(9)	C(10)
Signes attendus		+	?	+	-	+	?	+	+	+

Les résultats de l'estimation du modèle ECM se présentent comme suit : . Tableau 3 : Résultats de l'estimation du modèle à correction d'erreur (MCE)

Dependent Variable: D(INFL) Method: Least Squares Date: 07/29/04 Time: 09:42 Sample(adjusted): 1975 2003 Included observations: 29 after adjusting endpoints Convergence achieved after 11 iterations
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.079827	0.151107	0.528280	0.6038
D(LCE)	0.103169	0.045405	2.272181	0.0356
D(LPIBR)	0.039117	0.075643	0.517124	0.6114
D(LTXCHANGE)	-0.103281	0.037083	-2.785140	0.0122
INFL(-1)	-0.484210	0.127629	-3.793887	0.0013
LCE(-1)	-0.027115	0.021443	-1.264527	0.2222
LPIBR(-1)	0.073529	0.056306	1.305877	0.2080
LTXCHANGE(-1)	-0.067344	0.035119	-1.917608	0.0712
D75	-0.145822	0.062017	-2.351315	0.0303
D94	0.182009	0.063892	2.848709	0.0107
AR(1)	-0.536309	0.165253	-3.245387	0.0045
R-squared 0.881819 Mean dependent var -0.009792
Adjusted R-squared 0.816163 S.D. dependent var 0.106684
Durbin-Watson stat 1.959939 Prob(F-statistic) 0.000002
Inverted AR Roots -.54

Source : Traitement Eviews

D(INFL) = 0.08 + 0.10*D(LCE) + 0.04*D(LPIBR) - 0.10*D(LTXCHANGE) - 0.48*INFL(-1) - 0.03*LCE(-1) + 0.07*LPIBR(-1) - 0.07*LTXCHANGE(-1) - 0.14*D75 + 0.18*D94 + [AR(1)=-0.54]

Le test de racine unitaire effectué sur le résidu du modèle donne les résultats suivants:

ADF Test Statistic	-4.112020	1% Critical Value*	-3.6852
		5% Critical Value	-2.9705
		10% Critical Value	-2.6242

Source : Traitement Eviews

Les erreurs sont stationnaires, les variables INFL, LCE, LPIBR et LTXCHANGE sont bien cointégrées.

Le modèle ECM est valable et globalement satisfaisant, puisque le coefficient de correction d'erreur est négatif (-0,48) et significatif à 5%.

® Test d'homoscédasticité des erreurs

Pour tester une homoscédasticité éventuelle des erreurs, nous avons effectué le test de White. Les erreurs sont homoscédastiques si la probabilité est supérieure à 5%.

White Heteroskedasticity Test:
F-statistic Obs*R-squared	0.962092 16.29624	Probability Probability	0.538364 0.432483

Source : Traitement Eviews

Les résultats du test révèlent que les erreurs sont homoscédastiques car la probabilité est supérieure à 5%.

® Test d'autocorrélation des erreurs du modèle ECM

Pour vérifier si les erreurs sont autocorrélées ou non, nous avons réalisé le test de Breusch-Godfrey. La statistique de Breusch-Godfrey, donnée par BG = nR² suit un khi-deux à p degrés de liberté, avec :

p : nombre de retard des résidus

n : nombre d'observations

R² : coefficient de détermination

L'hypothèse de non-corrélation des erreurs est acceptée si la probabilité est supérieure à 5% ou si nR² < khi-deux lu.

Tableau : Résultat du test d'autocorrélation pour l'équation d'inflation

Breusch-Godfrey Serial Correlation LM Test:
F-statistic Obs*R-squared	0.015154 0.025828	Probability Probability	0.903470 0.872321

Source : Traitement Eviews

La probabilité étant supérieure à 5%, nous pouvons conclure que les erreurs ne sont pas corrélées. Les estimations obtenues sont donc optimales.

B 1 - Estimation de l'équation de croissance

L'estimation de l'équation de croissance suivra le même schéma que celle effectuée pour l'équation d'inflation. Les résultats des estimations et des tests seront présentés sans reprendre toute la théorie et la procédure qui guide ces tests. Deux variables muettes ont été introduites dans la spécification D78 et D98 en vue d'intégrer les chocs qu'ont subis l'économie béninoise en ces années. D78, pour apprécier l'impact de la deuxième crise pétrolière et D98 pour intégrer les effets de la crise énergétique de 1998.

a) Test de cointégration

1ère étape : Estimation par les M.C.O de la relation de long terme.

Elles a consisté en l'estimation de la relation de long terme du modèle de croissance, dont le résidu sera soumis au test d'ADF.

2ème étape : Test ADF sur le résidu

ADF Test Statistic	-4.396360	1% Critical Value*	-3.6752
		5% Critical Value	-2.9665
		10% Critical Value	-2.6220
*MacKinnon critical values for rejection of hypothesis of a unit root.

Source : Traitement Eviews

Le test ADF effectué sur le résidu indique que les séries PIBR, CE, INFL et INVTOTR sont cointégrées.

Ce résultat est du reste confirmé par le test de Johansen qui montre l'existence d'une seule relation de cointégration.

Tableau 4 : Résultat du test de cointégration de Johansen

Date: 07/29/04 Time: 12:54 Sample: 1972 2003
Included observations: 30
Test assumption: No deterministic trend in the data
Series: PIBR INFL CE INVTOTR
Lags interval: 1 to 1
	Likelihood	5 Percent	1 Percent	Hypothesized
Eigenvalue	Ratio	Critical Value	Critical Value	No. of CE(s)
0.458033	40.70648	39.89	45.58	None *
0.387863	22.32999	24.31	29.75	At most 1
0.194844	7.606002	12.53	16.31	At most 2
0.036145	1.104422	3.84	6.51	At most 3
*(**) denotes rejection of the hypothesis at 5%(1%) significance level
L.R. test indicates 1 cointegrating equation(s) at 5% significance level

Source : Traitement Eviews

Sur la base du résultat de ce test, nous pouvons donc utiliser la représentation à

correction d'erreur proposée par Engle et Granger.

b) Estimation du mécanisme à correction d'erreur (ECM)

D(PIBR) = C(1) + C(2)*D(CE) + C(3)*D(INFL) + C(4)*D(INVTOTR) + C(5)*PIBR(-1) + C(6)*INFL(-1) + C(7)*CE(-1) + C(8)*INVTOTR(-1) + C(9)*D78 + C(10)*D98 + [AR(1)=C(11)]

Dans cette expression, les coefficients C(1) à C(4) représente la dynamique de court terme, tandis que les coefficients C(6) à C(10) permettent de dériver les comportements d'équilibre de long terme. Le coefficient C(5) est le coefficient de correction d'erreur.

Les signes théoriques ci-après sont attendus :

Paramètre	C(1)	C(2)	C(3)	C(4)	C(5)	C(6)	C(7)	C(8)	C(9)	C(10)
Signes attendus		+	?	+	-	?	+	+	+	-

Les résultats de l'estimation du modèle ECM se présentent comme suit :

Tableau 5 : Résultats de l'estimation du modèle (MCE) de croissance

Dependent Variable: D(PIBR) Sample(adjusted): 1975 2003
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	52934.32	3335660.	0.015869	0.9875
D(CE)	0.275731	0.107320	2.569241	0.0193
D(INFL)	-67.79003	32.52148	-2.084469	0.0516
D(INVTOTR)	0.851707	0.210397	4.048104	0.0008
PIBR(-1)	-0.972445	0.043177	-22.52237	0.0000
INFL(-1)	-154.8910	58.22142	-2.660379	0.0159
CE(-1)	0.327311	0.184136	1.777552	0.0924
INVTOTR(-1)	0.942645	0.309858	3.042179	0.0070
D78	5.245724	9.112407	0.575668	0.5720
D98	-295.7222	13.79843	-21.43159	0.0000
AR(1)	0.999702	0.020957	47.70346	0.0000
R-squared	0.986020	Mean dependent var		22.95172
Adjusted R-squared	0.978254	S.D. dependent var		82.38834
Log likelihood	-106.6551	F-statistic		126.9580
Durbin-Watson stat	2.159362	Prob(F-statistic)		0.000000
Inverted AR Roots	1.00

Source : Traitement Eviews

D(PIBR) = 52934.3 + 0.28*D(CE) - 67.8*D(INFL) + 0.85*D(INVTOTR) - 0.97*PIBR(-1) - 154.9*INFL(-1) + 0.33*CE(-1) + 0.94*INVTOTR(-1)

+ 5.25*D78 - 295.72*D98 + [AR(1)=0.99]

Le test de racine unitaire effectué sur le résidu du modèle donne les résultats suivants:

ADF Test Statistic	-4.074406	1% Critical Value*	-3.6852
		5% Critical Value	-2.9705
		10% Critical Value	-2.6242
*MacKinnon critical values for rejection of hypothesis of a unit root.

Source : Traitement Eviews

Les erreurs sont stationnaires, les variables PIBR, INFL, CE, et INVTOTR sont

bien cointégrées.

Le modèle ECM est valable, le coefficient de correction d'erreur est significativement négatif et le modèle ECM est validé.

® Test d'homoscédasticité des erreurs

Le test de White permet de vérifier une homoscédasticité éventuelle des erreurs

White Heteroskedasticity Test:
F-statistic Obs*R-squared	0.841643 15.33488	Probability Probability	0.633294 0.500262

Source : Traitement Eviews

Les résultats du test révèlent que les erreurs sont homoscédastiques car la probabilité est supérieure à 5%.

® Test d'autocorrélation des erreurs du modèle ECM

Le test de Breusch-Godfrey est vérifier une éventuelle autocorrélation des erreurs.

Tableau : Résultat du test d'autocorrélation pour l'équation de croissance

Breusch-Godfrey Serial Correlation LM Test:
F-statistic Obs*R-squared	2.071287 3.149027	Probability Probability	0.168254 0.075972

Source : Traitement Eviews

La probabilité étant supérieure à 5%, nous pouvons conclure que les erreurs ne sont pas corrélées. Les estimations obtenues sont donc optimales.

Les modèles retenues étant significatifs sur le plan statistique qu'économique, nous allons procéder à l'analyse des résultats obtenus.

⁸ Test de Jarque Bera

SECTION 2 : ANALYSE DES RESULTATS Paragraphe 1 : Modèle d'inflation

Les résultats ci-dessus montrent que les variables exogènes retenues, à savoir, les crédits à l'économie (CE), le PIB réel (PIBR) et le taux de change (TXCHANGE) expliquent 82% du comportement de l'inflation au Bénin. Tous les coefficients estimés présentent les signes attendus, à l'exception, toutefois de celui du taux de change dont le signe négatif obtenu est contraire aux hypothèses théoriques. Le premier choc pétrolier (D75) ainsi que le changement de parité du FCFA (D94) ont effectivement impacté l'inflation au Bénin.

A court terme que dans le long terme, toutes les variables explicatives sont significatives, à l'exception du PIB réel. L'élasticité des crédits par rapport à l'inflation ressort à 0,10. Ainsi, la réponse à un accroissement net de 1% des crédits à l'économie induit un relèvement de 0,10% de l'inflation. Cependant, à long terme, cette variable exerce un impact plus faible sur l'inflation (élasticité de long terme égale 0,055). Ce résultat dénote de l'efficacité globale de la politique de la monnaie et du crédit de la BCEAO sur la période d'étude, en matière de maîtrise de l'inflation.

S'agissant du PIB réel, la non-significativité statistique de cette variable vient corroborer les résultats des travaux de Kako (2001). Elle s'expliquerait par la non-prise en compte, dans le modèle des déterminants non-monétaire de l'inflation.