2.3 Conclusion :
Dans cette partie nous avons posé le problème
traité avec les conditions aux limites correspondantes. Dans le prochain
chapitre nous allons exploiter les équations d'équilibre et les
conditions aux limites pour établir l'équation
intégrale.
CHAPITRE 3
DERIVATION DE L'EQUATION INTEGRALE
3.1 Introduction :
Dans cette partie nous allons utiliser les équations
d'équilibre (2.11) établies dans le chapitre
précédent relativement à la phase de propagation et les
conditions aux limites correspondantes pour établir l'équation
intégrale, les équations d'équilibre sont
transformés a l'aide de la transformée de Fourier standard en une
équation intégrale suivant les travaux de ERDOGAN [18].
3.2 Les données de la transformation :
Pour obtenir l'équation intégrale pour le
système (2.11) on réécrit toutes les conditions
|
aux limites sur l'axe x2 = 0 et les bords
x1 = #177;h:
|
|
|
|
|
|
223 (x1 ,0+ ) =
223 (x1 ,0 - ) =
|
2(x1
|
),
|
x1 </a,
|
(3.1)
|
|
223 (x1 , h) = 223 (x1
,-h) =
|
0,
|
x1 <
|
+00,
|
(3.2)
|
|
223 (x1,0+) =223(x1, 0 ),
|
x1
|
> /a
|
|
(3.3)
|
|
w(x1,0+)=
w(x1,0-),
|
x1
|
> /a
|
|
(3.4)
|

le
si
xi
(3.5)
si
la
le
<xi
48
Ou :
r(xi)
~--r00 ,
= ~
~ --+rc,
Avec la relation de l'élasticité suivante :
aw(xi , x2)
r23 = (3.6)
ax2
Appliquant la transformée de fourrier sur la solution du
problème. La transformé de fourrier est définis comme suit
:
Sous forme paramétrique :
Soit une fonction a deux variables f (xi ,
x2) , on prend x2 comme paramètre, la
transformé de fourrier est donné par :
+00
|
U
f (2, x
|
2) = ff(xi,x2).e--axi .
|
dx1 (3.7)
|
--00
Ou bien, en considérons les deux variables : Soit une
fonction h(xi , x2) :
+00+00
= f fh(xi , x2 ).e-i.(2.xi +e.x2)
.dx1.dx2.
(3.8)
--00-- 00
La transformé de fourrier inverse :
2
= f7(2 d2 p --00
f(xi,x2)
1

(3.9)
L'équilibre est donné par l'équation
suivante :
Aw = 0 (3.10)
a 2
w+ a2w = 0 (3.10 bis)
2 2
axax
; 2
+00
a 2 --w(2, x, ) ;2
-- 22 f w(2, x2 d. ax
1,+ f d2 = 0
«
2
+00 +00
--00 --00
(3.12)
(a2w(2, x2
22w(2, x2 = 0
ax;
--00
(3.13)
+00
f
a 2 1 +00 a 2 1
(3.11)
2 ( fw(2, x2
).Ciasi d2) + 2 ( fw(2,
x2 ).Ci2si d2) = 0
ax 271---00 ax2 271---00
|
2
W(2, x2) 22
2, 0
W(x2)
|
49
(3.14)
|
|
axe
|
|
Sous la forme :
|
|
|
f cents- 22 .f =0
|
(3.15)
|
|
L'équation caractéristique donne :
|
|
|
n 2 -22 = 0, = 1.2
|
(3.16)
|
|
n 1 = - 2n, 2 = 2
|
(3.17)
|
|
La solution est de la forme suivante :
|
|
|
W(2, x2) = C1
(2).e"2 + C2 (2).en2.x2
|
(3.18)
|
En appliquant la transformé de fourrier inverse sur la
solution on obtient les différentes expressions pour la solution au
dessus et au dessous de la fissure :
+00
w(x1,x2) = 27/- f(C1
(2).en1.x2 + C2 (2).en2.x2
.d2, 0 < x2 < h (3.19)
-00
1 +00
w(x1,x2)= 27/-
f(C3(2).e"2
+C4(2).en2s2).e-L2s1 - h
< x2 < 0 (3.20)
-00
Ou C k (2) , (k =1,.......,4) sont les
fonctions inconnues de la variable 2 déterminées en
utilisant les conditions aux limites (3.1) et (3.2), et n1,
n2 sont les racines du polynôme caractéristique
relative a l'opérateur A, ils sont données par :
|
n2 - 22 = 0,
|
n1=
|
2,
|
n2
|
= -
|
2
|
|
(3.21)
|
De l'équation (3.2) (3.3) et (3.20) il est facile de
trouver :
C 1 e 2.h .h
-C2.e-= 0 (3.22)


C3.e-2.h C
4.e2.h =0
(3.23)


Pour réduire le problème à une
équation intégrale, on introduit la fonction densité
suivante :
d
W(x1) =
dx[w(x1,0+)-w(x1,0-)1
(3.24)
fv(t).dt = 0, v(x1) = 0 Pour (3.25)
En substituent les équations (3.19) (3.20) dans (3.4), on
obtient :
W(x) =211-
fi2(C1+ C2 -- C3 --
00
En prenant la transformée de fourrier inverse, on obtient
:
1o
i.2.(C1 + C2 -- C3 --
C4) = .dt
1o
.dt (3. 26)
C1 + C2 -- C3 -- C4
= 2. fv(t).ei.2.t
o
1
Notons le second membre de (3.26) par F :
+1
F =ifvf(t).ei.2.t .dt
(3. 27)
De l'égalité (3.3) :
1-23 (x1 , )
2.x2 -- e 2.x2 ).e--i.a.x1
x2 > 0


2.
.
+00
e
.
(C1
Dr
00 +00
1-23 (x1, x ) = . f(C 2 --
.x2).e--i.2.x1
j2el" e 4
00
|
x2 < 0
|
+00 +00
2
. 2. f(C1--C2 ).e--i.2.x1
.d2= . . f(C3 -- C4
).e--i.a.x1 .d2
Dr


--00 --00
C1--C2--C3+C4=0 (3.28)
Pour trouver les valeurs des C k ,(k =1,........,4).
il suffit de résoudre le système d'équations
algébriques suivants :
.e
C3 .e--2.h
C4e
.
+
C2- C3
C2 - C3 + C4

0
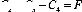

.h
.h
2
0
C2
.e
2

.h
2
0
- C4 = F
(3. 29)
51
Nous avons trouvé :
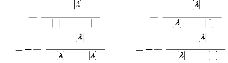
.
h
F.e
h
.h +e .
.
h
1
F.e
.
+e
- C2 =1
- .h
2. - e
.
h
F.e
C4
F.e
.
h
1
-
.
=
.
h
-
2 e
.h +e .
.
. ,
-
h
h
.
+e
2 e
=
=
C 1
C3
.
2 e
1
(3.40)
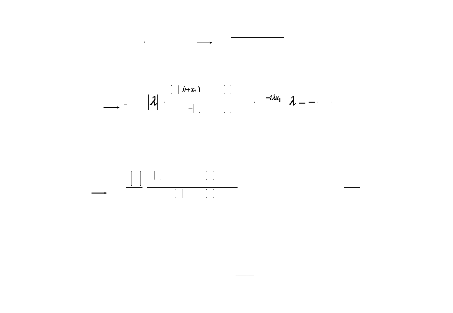
Substituant les constantes C3 et C4 dans
l'équation suivante :
9
(x1,0- )=x2 W( = 1-(x1 )
axX1 X22
1-23
On obtient :
4,r
=
d
t ( )
x 1
m
- (h+x2)
(e - e
- h +e h )e
2
e
+00
0
x2
lim
IF
- 00
On substituent F de l'équation (3.27) et en changent
l'ordre d'intégration:
lo +00 e (h+x2) - e- (h+x2)
f(x2lim0- f - h h )ei (t-x1)
camodt = - 1-(x1e + e m
- l -00
o
Mettons l'équation sous la forme suivante :
l of k(x1,t).v(t).dt =-4
.1-(x) (3. 41)
m-l o
Avec :
)
+00 e .(h+ x2) - e- .(h+x2) -
k(x1 ,t)= x2lim 0- fi. .(
- .h h
e +e
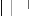


-00
. d (3. 42)
Notons par (x1Hla, ) partie sous le signe
d'intégration dans l'équation précédente :
)
+x2
.
h
.
(x2, ) --
--h - .
e + e
.(h+x2) - .(h-e
e
h+x
(3.43)
(x2, ) = -H(x2,- )
L'intégrale (3,43) devient :
|
k(Xi , t On sait que :
|
)
|
+ - - -
ea...(h+X2) - e-2.(h+X2) e e
i t X i t X
=2.( -2.h 2.h ).( ).d.1.
(3.22.44)
X2m0- 2
e + e i
0
|

-
i.X
ei.X - e
X
=
i
sin(
)
2.
D'où :
+2(h+X2) -2.(h+X2)
). sin 2.(t - X).d2 (3.23.45)
6
k(Xi,t)= X2lim0- - 2 f.( e 2.h
0
e + e
k(Xi,t) Se réduit a :
+-2.(h+X2) +
(3.24.46)
k(X
1,0= Xlim0-(-2 f(ea.X
e 2 e
0
-.1. h h.sin(2.(t-X1))).d2
· + e2
·
)
L'équation intégrale devient :
~ ~fk' (Xi,t).v(t).dt
=2.n- . ( ) .(3.25.47)
m-~ ~
Avec
+ -e
h+X2) + e-2.(h-X2
k (X,t)=X lim ( . f(ea X2
0
e
2 +e
l .(
0
|
)
|
).sin(2.(t - Xi))).
|
dit (3.26.48)
|
Le premier terme donne :
+X2 lim 0- fea.X2
.sin(.1(t -X))4.1. = 1
(3.27.49)

t - X1
Notons par I la partie suivante :
|
1= lim
2
|
+-2.(h+X2)+ e -2.(h-X2)
2e-.1h0-( f( e
-a.h + e a.h ). sin(2.(t e + e
)))d2 = sin(2(t - ))
00
|
dit (3.28.50)
|
+00
0
Finalement, l'équation intégrale s'écrit
:
1o
f
) (3.29.51)
( 1 + k" (x1,t))v(t)dt
=271- «x1

Il
t-x1
1o
Avec : fvf(t)dt = 0
-1 o
2h
2e-
k" (x1, t) =-f -tee », sin(2(t
- x1 ))dt e +e
| 


